Radio (geometría)

Elementos principales del círculo

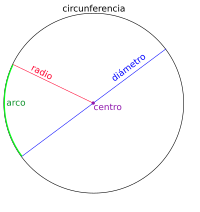
En geometría clásica, el radio de una circunferencia es el lugar geométrico de los puntos del plano que equidistan de otro punto llamado centro; o también se puede definir como: cualquier recta punto o segmento que va desde su centro a cualquier punto de la circunferencia. Un radio de una esfera es cualquier segmento que va desde su centro a su superficie. Por extensión, el radio de una circunferencia o esfera es la longitud de cualquiera de sus radios. El radio es la mitad del diámetro. En ciencia e ingeniería se suele usar el término radio de curvatura como sinónimo de radio.

En un sentido más general —en geometría, ingeniería, teoría de grafos y muchos otros contextos—, el radio de algo (por ejemplo, de un cilindro, un polígono, un grafo o una parte mecánica) es el segmento que une cualquier punto de la circunferencia con su centro o eje y sus puntos más externos. En estos casos, el radio es la mitad desde un angulo de la circunferencia hacia su centro En un polígono regular es la distancia que une su centro con uno de los vertices o extremos. No se debe confundir este con la apotema que es la distancia entre el centro y cualquiera de sus lados

La relación entre el radio y el perímetro de un círculo es $r={\frac {p}{2\pi }}$.

La relación entre el radio y el área de un círculo es $r={\sqrt {\frac {a}{\pi }}}$.

== Véase también ==Error al representar (error de sintaxis): {\displaystyle Escribe aquí una fórmula}

• Diámetro
• Círculo
• Circunferencia
• Apotema
• Polígono