Proporción (arquitectura)

La proporción es un principio central de la teoría de la arquitectura y una conexión importante entre matemáticas y arte. Es el efecto visual de las relaciones de los diversos objetos y espacios que componen una estructura entre sí y con la totalidad del conjunto. Estas relaciones a menudo se rigen por múltiplos de una unidad estándar de longitud conocida como "módulo".^[1]

La proporción en arquitectura fue discutida por destacados arquitectos de todas las épocas, como Vitruvio, Leon Battista Alberti, Andrea Palladio y Le Corbusier entre otros.

Arquitectura romana

Vitruvio

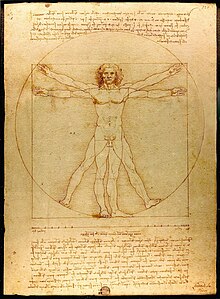
La arquitectura en la antigüedad romana rara vez se documentaba, con la notable excepción del 'tratado' De architectura escrito por de Vitruvio, quien se formó como ingeniero en las legiones de Julio César durante las primeras guerras en las Galias (58-50 a. C.). El tratado estaba dedicado al emperador Augusto. Cuando Vitruvio definió los conceptos fundamentales en los primeros capítulos del tratado, mencionó que los tres requisitos básicos de la arquitectura son firmeza (firmitas), utilidad (utilitas) y belleza (venustas), que requieren que los arquitectos estén equipados con un tipo variado de aprendizajes y de conocimientos procedentes de muchas ramas. Además, identificó los "Seis Principios del Diseño" como orden (ordinatio), disposición (dispositio), proporción (eurythmia), simetría (symmetria), propiedad (decor) y economía (distributio). Entre los seis principios, la proporción se interrelaciona y apoya a todos los demás factores a través de formas geométricas y proporciones aritméticas.^[2]

La palabra "simetría", generalmente traducida literalmente como "simetría" en las versiones modernas, en la antigüedad significaba algo más relacionado con la "armonía matemática"^[3] y con la modularidad de las proporciones. Vitruvio trató de describir su teoría en la composición del cuerpo humano, al que se refirió como la proporción perfecta o áurea. Los principios de las unidades de medida de dedos, pies y codos también provienen de las dimensiones del Hombre de Vitruvio. Más específicamente, Vitruvio usó la altura total de 6 pies de una persona, y cada parte del cuerpo toma una proporción diferente. Por ejemplo, la cara mide aproximadamente 1/10 de la altura total y la cabeza mide aproximadamente 1/8 de la altura total.^[3] Vitruvio usó estas proporciones para demostrar que la composición de los órdenes clásicos imitaba al cuerpo humano, asegurando así la armonización estética cuando se percibía la forma de las columnas diseñadas arquitectónicamente.^[2]

Arquitectura clásica

En la arquitectura clásica, el módulo se establecía como el radio del eje inferior de una columna clásica, con proporciones expresadas como fracciones o múltiplos sencillos de ese módulo.^[4]

Renacimiento

El estudio de la proporción se convirtió en un asunto de gran importancia en la arquitectura del Renacimiento, siguiéndose distintos enfoques:

En sus “Cuatro libros sobre arquitectura”, Andrea Palladio establece una jerarquía de proporciones espaciales que se remonta directamente a Platón.^[5] "Hay siete tipos de estancias más bellos y mejor proporcionados...":

La habitación es redonda o cuadrada porque los bordes están a la misma distancia de su centro.
El cuadrado se alarga sobre su diagonal (proporción desde la raíz de 2), relación 1:1,41...).
La longitud es 1 1/3 de su ancho (relación: 3:4 o 1:1,33; musical: cuarta).
La longitud es 1 1/2 de su ancho (relación: 2:3 o 1:1,50; musical: quinta).
La longitud es 1 2/3 de su ancho (relación: 3:5 o 1:1,67; musicalmente: sexta mayor).
La longitud es de dos cuadrados (proporción: 1:2; musicalmente: octava).^[6]

En sus "Cuatro libros" hay una serie de diseños de villas y palacios, como el Palacio Antonini que muestra como el primer ejemplo, cuyas estancias están proporcionadas de acuerdo con estas categorías. La altura de las habitaciones corresponde a su ancho, la altura del suelo de la mezanina debe ser un sexto menor que la del suelo principal de abajo.

Dibujo con las proporciones de las raíces, comenzando con el cuadrado (lado 1)

Daniele Barbaro y Andrea Palladio tradujeron el tratado de Vitruvio del latín al italiano y lo complementaron con métodos matemáticos y geométricos, así como dibujos de geometría y arquitectura. También describieron las proporciones de las diagonales (raíces cuadradas), que dan a los arquitectos proporciones adicionales para un diseño armonioso. El procedimiento consiste en partir de un cuadrado, cuya diagonal se abate sobre el lado contrario con un compás, para crear la proporción 1:√2 (1:1,414..). El rectángulo recién formado se vuelve a abatir por su diagonal, y se crea un nuevo triángulo de proporción 1:√3 (1:1,732..). De esta manera, se obtienen las proporciones √4, √5,... √n una tras otra.

Dado que las proporciones de las raíces generalmente generan números inconmensurables, en el pasado se usaron aproximaciones que eran lo suficientemente precisas para los constructores de la época:

√2; de 1,414:1 se convirtió en 7:5 o 17:12 o 21:15
√3; de 1,732:1 se convirtió en 7:4 o 12:7
√5; de 2,236:1 se convirtió en 20:9
√6; de 2,449:1 se convirtió en 17:7 o 22:9

Las proporciones de la raíz también se volvieron más fáciles de manejar a través de aproximaciones:

√3:√2; de 1,723:1,414 se convirtió en 26:21
√4:√3; de 2000:1723 se convirtió en 7:6 u 8:7 o 15:13
√4:√3:√2:√1 se convirtió en 30:26:21:15

Palladio especificó las dimensiones 30:26:21:15 pies Vicentinos (aproximadamente de 34,7 cm)^[7] para su diseño de la famosa Villa Capra.^[8]^[9]

Para armonizar la multitud de diferentes proporciones, Alberti y Palladio describieron la aplicación de distintas medias construibles con regla y compás. Por ejemplo, la media aritmética (promedio) de la longitud y el ancho de un plano de planta se determina matemáticamente o geométricamente para encontrar la altura de la habitación o la proporción de la habitación siguiente. Ambos arquitectos también describen la media geométrica y la media armónica para disponer de una mayor variedad de relaciones.^[10]

Le Corbusier

Artículo principal: Modulor

En su obra Le Modulor (1948), Le Corbusier presentó un sistema de proporciones que tomó el número áureo y un hombre con un brazo levantado como los módulos escalables de la proporción.

Véase también

Referencias

↑ James Stevens Curl (ed.), Oxford Dictionary of Architecture, 2nd ed. (Oxford, 2006), 606-607.
↑ ^a ^b Jones, Mark Wilson (2000). Principles of Roman Architecture. New Haven and London: Yale University Press. pp. 33–46. ISBN 978-0-300-08138-1.
↑ ^a ^b Jones, Mark Wilson (2000). Principles of Roman Architecture. New Haven and London: Yale University Press. pp. 41. ISBN 978-0-300-08138-1.
↑ James Stevens Curl (ed.), Oxford Dictionary of Architecture, 2nd ed. (Oxford, 2006), 496.
↑ Plato, Timaios c7 bis c20
↑ Andrea Palladio: Vier Bücher zur Architektur. Venedig 1570. (dt. München/ Zürich 1983, ISBN 3-7608-8116-5)
↑ Roger Popp: Die Mittelmaße in der Architektur. Hamburg 2005, ISBN 3-8300-1973-4.
↑ Andrea Palladio: Die vier Bücher zur Architektur. Zürich/ München 1983, ISBN 3-7608-8116-5, S. 133.
↑ Lionel March: Architectonics of Humanism. Chichester (West Sussex) 1998.
↑ Roger Popp: Die Mittelmaße in der Architektur - Wesen, Bedeutung und Anwendung von der Antike bis zur Renaissance. Hamburg 2005, ISBN 3-8300-1973-4.

Lecturas relacionadas

P. H. Scholfield (1958). The Theory of Proportion in Architecture. Cambridge University Press.
Hanno-Walter Kruft (1994). History of Architectural Theory. Princeton Architectural Press. ISBN 9781568980102.

Datos: Q47694

[1] James Stevens Curl (ed.), Oxford Dictionary of Architecture, 2nd ed. (Oxford, 2006), 606-607.

[:0-2] Jones, Mark Wilson (2000). Principles of Roman Architecture. New Haven and London: Yale University Press. pp. 33–46. ISBN 978-0-300-08138-1.

[:1-3] Jones, Mark Wilson (2000). Principles of Roman Architecture. New Haven and London: Yale University Press. pp. 41. ISBN 978-0-300-08138-1.

[4] James Stevens Curl (ed.), Oxford Dictionary of Architecture, 2nd ed. (Oxford, 2006), 496.

[5] Plato, Timaios c7 bis c20

[6] Andrea Palladio: Vier Bücher zur Architektur. Venedig 1570. (dt. München/ Zürich 1983, ISBN 3-7608-8116-5)

[7] Roger Popp: Die Mittelmaße in der Architektur. Hamburg 2005, ISBN 3-8300-1973-4.

[8] Andrea Palladio: Die vier Bücher zur Architektur. Zürich/ München 1983, ISBN 3-7608-8116-5, S. 133.

[9] Lionel March: Architectonics of Humanism. Chichester (West Sussex) 1998.

[10] Roger Popp: Die Mittelmaße in der Architektur - Wesen, Bedeutung und Anwendung von der Antike bis zur Renaissance. Hamburg 2005, ISBN 3-8300-1973-4.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]