Problema de la secretaria

Gráficos de probabilidades de obtener el mejor candidato (círculos rojos) de n solicitudes y k/n (cruces azules) donde k es el tamaño de la muestra

El problema de la secretaria (en inglés: Secretary problem)​​ demuestra un escenario que involucra la teoría de parada óptima​​ que se estudia ampliamente en los campos de la probabilidad aplicada, la estadística y la teoría de la decisión. También se le conoce como el problema del matrimonio, el problema de la dote del sultán, el problema del pretendiente quisquilloso, y el problema de la mejor elección.​​​​ Su solución también se conoce como regla del 37%.​​​

El problema de la secretaria aparentemente fue introducido en 1949 por Merrill M. Flood, quien lo llamó el problema de la prometida en una conferencia que dio ese año. Se refirió a él varias veces durante la década de 1950, por ejemplo, en una conferencia en la universidad Purdue el 9 de mayo de 1958, y finalmente se hizo ampliamente conocido en el folclore, aunque no se publicó nada en ese momento. En 1958 envió una carta a Leonard Gillman, con copias a una docena de amigos, entre ellos Samuel Karlin y J. Robbins, esbozando una prueba de la estrategia óptima, con un apéndice de R. Palermo que demostró que todas las estrategias están dominadas por una estrategia de la forma "rechazar la primera p incondicionalmente, luego aceptar al siguiente candidato que sea mejor".​

Al parecer, la primera publicación fue de Martin Gardner en Scientific American, febrero de 1960. Se había enterado de ello por John H. Fox Jr. y L. Gerald Marnie, quienes de forma independiente habían ideado un problema equivalente en 1958; Lo llamaron "game of googol". Fox y Marnie no conocían la solución óptima; Gardner pidió consejo a Leo Moser, quien (junto con J. R. Pounder) proporcionó un análisis correcto para su publicación en la revista. Poco después, varios matemáticos escribieron a Gardner para contarle sobre el problema equivalente que habían escuchado a través de los rumores, todo lo cual probablemente se remonta al trabajo original de Flood.​ La ley 1/e de mejor elección se debe a F. Thomas Bruss.​

Ferguson tiene una extensa bibliografía y señala que un problema similar (pero diferente) había sido considerado por Arthur Cayley en 1875 e incluso por Johannes Kepler mucho antes, quien pasó dos años investigando a 11 candidatos al matrimonio durante 1611-1613 después de la muerte de su primera esposa.​

Definición

Vemos un caso particular de distribución de las secretarias

Vemos cómo la gráfica de las p(k) se aproxima a la de -x/n·ln(x/n)

Su enunciado es el siguiente:

Supongamos que tenemos que elegir secretaria de entre 100 candidatas. Solo podemos entrevistar a cada persona una vez. Después de cada entrevista, hay que decidir si la contratamos o no. Si decidimos que no, perdemos la oportunidad para siempre. Si entrevistamos a 99 sin haber elegido, tenemos que contratar a la número 100.

Cabría pensar que la probabilidad de contratar la secretaria ideal es de 1 entre 100, pero lo cierto es que podemos hacerlo mucho mejor.

Entrevistemos a la mitad de las personas y detengámonos después en la  siguiente mejor, es decir, la primera que sea mejor que la mejor de las ya entrevistadas. Una cuarta parte de las veces, la segunda mejor estará entre las 50 primeras y la mejor de todas en las 50 segundas. De manera que al menos el 25 por ciento de las veces la regla de «parar en la siguiente mejor» dará como resultado contratar a la mejor secretaria.

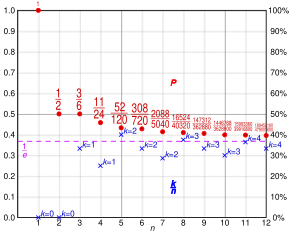
Y es posible hacerlo aún mejor. John Gilbert y Frederick Mosteller, de la Universidad de Harvard, demostraron que es posible aumentar la probabilidad entrevistando a 37 personas y luego parando en la siguiente mejor que las 37 entrevistadas. La probabilidad de coger a la mejor secretaria con esta estrategia del 37 es aproximadamente el 37% .El número 37 proviene de dividir 100 entre e, la base de los logaritmos naturales.​

Solución

La estrategia es fijar un número k y después de la entrevista kª contrataremos a la próxima persona que mejore a las entrevistadas hasta entonces. Calcularemos la probabilidad de ganar con cada número k fijado y tomaremos el valor que maximice la probabilidad de ganar.

Fijamos pues un número k y calculemos ahora la probabilidad de ganar.

Sea D la posición de la secretaria ideal

p(ganar)= $\sum _{i=k+1}^{100}$ p(ganar/(D=i))·p(D=i)

Pues si $i\leq k$, p(ganar/(D=i))=0, pues D$\leq$k implica que la entrevista a la mejor pasó ya y fue rechazada.

Es fácil ver que p(D=i)=1/100

Ganaremos si la mejor secretaria de las primeras i-1 está entre las k primeras, pues sino la escogeremos y perderemos y por el mismo método que calculamos p(D=i)=1/100, pues ahora concluimos que

p(ganar/(D=i))=k/(i − 1)

La probabilidad de ganar es

$\sum _{i=k+1}^{100}$ k/(i-1) · 1/100 = k/100 · (SA(100)-SA(k))

Designando por SA(m) la serie armónica hasta m:

1+1/2+1/3+ ... +1/m

sumas que se aproximan con el logaritmo neperiano

Así la probabilidad de ganar para n grande (en nuestro caso n=100) es aproximadamente

k/n · (ln(n)-ln(k)) = - k/n · (ln(k)-ln(n)) = - k/n · (ln(k/n))

Para maximizar esta función de k derivamos y igualamos a cero

-1/n ·  (ln(k/n)) - k/n · 1/n·n/k = 0

(ln(k/n)) + 1 = 0

k/n = 1/e

k = n/e

Bibliografía

• F. Thomas Bruss. "The art of a right decision: Why decision makers want to know the odds-algorithm." Newsletter of the European Mathematical Society, Issue 62, 14–20, (2006)
• Rogerson, R.; Shimer, R.; Wright, R. (2005). «Search-theoretic models of the labor market: a survey». Journal of Economic Literature 43 (4): 959-88. JSTOR 4129380. doi:10.1257/002205105775362014. 
• El maravilloso mundo de las matemáticas. New Scientist, sección Matemáticas cotidianas, saber cuando parar. ISBN ebook: 978-84-114-8385-8

Enlaces externos con animaciones

• Explicación y simulaciones del problema realizadas con Descartes JS
• Trabajo fin de grado sobre este problema, Universidad de la Laguna

• Datos: Q1372364