Polinomios de Macdonald

En matemáticas, los polinomios de Macdonald P_λ(x; t,q) son una familia de polinomios ortogonales simétricos en varias variables, introducidos por Macdonald en 1987. Más tarde introdujo una generalización no simétrica en 1995. Macdonald originalmente asoció sus polinomios con pesos λ de sistemas de raíz finitos y usó solo una variable t, pero luego se dio cuenta de que es más natural asociarlos con un sistema de raíces afines en lugar de con un sistema de raíces finitas, en cuyo caso la variable t puede ser reemplazada por varias variables diferentes t=(t₁,...,t_k), una para cada una de las órbitas k de las raíces en el sistema de raíces afines. Los polinomios de Macdonald son polinomios en n variables x=(x₁,...,x_n), donde n es el rango del sistema de raíces afines. Generalizan muchas otras familias de polinomios ortogonales, como el polinomio de Jack, el polinomio de Hall-Littlewood y los polinomios de Askey-Wilson, que a su vez incluyen la mayoría de los polinomios ortogonales de una variable nombrados como casos especiales. Los polinomios de Koornwinder son polinomios de Macdonald de ciertos sistemas de raíces no reducibles. Tienen relaciones profundas con álgebra de Hecke afín y con el esquema de Hilbert, que se utilizaron para probar varias conjeturas hechas por Macdonald sobre ellos.

Definición

Primero, para manejar con mayor facilidad las expresiones, debe establecerse una notación específica:

• R es un sistema de raíces finito en un espacio vectorial real V.
• R⁺ es una elección de raíces positivas, a la que corresponde un grupo de Weyl positivo.
• W es el grupo de Weyl de R.
• Q es el retículo raíz de R (el retículo atravesado por las raíces).
• P es el retículo de ponderación de R (que contiene a Q).
• Un orden en la ponderación: $\mu \leq \lambda$ si y solo si $\lambda -\mu$ es una combinación lineal no negativa de raíces simples.
• P⁺ es el conjunto de pesos dominantes: los elementos de P en la cámara de Weyl positiva.
• ρ es el vector de Weyl: la mitad de la suma de las raíces positivas; este es un elemento especial de P⁺ en el interior de la cámara de Weyl positiva.
• F es un campo de característica 0, normalmente los números racionales.
• A = F(P) es el grupo algebraico de P, con una base de elementos denominada e^λ para λ ∈ P.
• Si f = e^λ, entonces f significa que e^−λ, y esto se extiende por linealidad a todo el álgebra de grupos.
• m_μ = Σ_{λ ∈ Wμ}e^λ es una suma de órbitas; estos elementos forman una base para la subálgebra A^W de elementos fijados por W.
• $(a;q)_{\infty }=\prod _{r\geq 0}(1-aq^{r})$, el símbolo q-Pochhammer del infinito.
• $\Delta =\prod _{\alpha \in R}{(e^{\alpha };q)_{\infty } \over (te^{\alpha };q)_{\infty }}.$
• $\langle f,g\rangle =({\text{término constante de }}f{\overline {g}}\Delta )/|W|$ es el producto interno de dos elementos de A, al menos cuando t es una potencia entera positiva de q.

Los polinomios de Macdonald P_λ para λ ∈ P⁺ están definidos únicamente por las siguientes dos condiciones:

$P_{\lambda }=\sum _{\mu \leq \lambda }u_{\lambda \mu }m_{\mu }$ donde u_λμ es una función racional de q y t con u_λλ = 1;

P_λ y P_μ son ortogonales si λ < μ.

En otras palabras, los polinomios de Macdonald se obtienen ortogonalizando la base obvia para A^W. La existencia de polinomios con estas propiedades es fácil de demostrar (para cualquier producto interior). Una propiedad clave de los polinomios de Macdonald es que son ortogonales: 〈P_λ, P_μ〉 = 0 siempre que λ ≠ μ. Esta no es una consecuencia trivial de la definición porque P⁺ no está totalmente ordenado, por lo que tiene muchos elementos que no son comparables. Por tanto, hay que comprobar que los polinomios correspondientes siguen siendo ortogonales. La ortogonalidad se puede probar mostrando que los polinomios de Macdonald son vectores propios para un álgebra de conmutación de operadores autoadjuntos con espacios propios unidimensionales, y utilizando el hecho de que los espacios propios para diferentes valores propios deben ser ortogonales.

En el caso de sistemas de raíces no simplemente entrelazados (B, C, F, G), el parámetro t se puede elegir para variar con la longitud de la raíz, dando una familia de tres parámetros de polinomios de Macdonald. También se puede extender la definición al sistema raíz no reducido BC, en cuyo caso se obtiene una familia de seis parámetros (una t para cada órbita de las raíces, más q) conocida como los polinomios de Koornwinder. A veces es mejor considerar que los polinomios de Macdonald dependen de un sistema de raíces afines posiblemente no reducido. En este caso, hay un parámetro t asociado a cada órbita de raíces en el sistema de raíces afines, más un parámetro q. El número de órbitas de las raíces puede variar de 1 a 5.

Ejemplos

• Si q = t los polinomios de Macdonald se convierten en los caracteres de Weyl de las representaciones del grupo compacto del sistema de raíces, o las funciones de Schur en el caso de sistemas de raíces de tipo A.
• Si q = 0 los polinomios de Macdonald se convierten en las funciones esféricas zonales (reescalados) para un grupo semisimple p-ádico, o los polinomios de Hall-Littlewood cuando el sistema de raíces es de tipo A.
• Si t=1 los polinomios de Macdonald se convierten en las sumas sobre las órbitas W, que son las funciones simétricas del monomio cuando el sistema de raíces es de tipo A.
• Si se hace que t = q^α y que q tienda a 1, los polinomios de Macdonald se convierten en los polinomios de Jack cuando el sistema de raíces es del tipo A, y en los polinomios de Heckman-Opdam para sistemas más generales de raíces.
• Para el sistema de raíces afines A₁, los polinomios de Macdonald son los polinomios de Rogers.
• Para el sistema de raíces afines de rango 1 no reducible del tipo (C∨
  1, C₁), los polinomios de Macdonald son los polinomios de Askey-Wilson, que a su vez incluyen como casos especiales la mayoría de las familias nombradas de polinomios ortogonales de una variable.
• Para el sistema raíz afín no reducido de tipo (C∨
  n, C_n), los polinomios de Macdonald son los polinomios de Koornwinder.

Conjetura del término constante de Macdonald

Si t = q^k para algún entero positivo k, entonces la norma de los polinomios de Macdonald viene dada por

$\langle P_{\lambda },P_{\lambda }\rangle =\prod _{\alpha \in R,\alpha >0}\prod _{0<i<k}{1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))+i} \over 1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))-i}}.$

Esto fue conjeturado por Macdonald (1982) como una generalización de la conjetura de Dyson, y Cherednik (1995) lo demostró para todos los sistemas de raíces (reducidos) usando las propiedades del álgebra de Hecke doblemente afín. La conjetura había sido probada previamente caso por caso para todos los sistemas de raíces excepto los del tipo E_n por varios autores.

Hay otras dos conjeturas que, junto con la conjetura de la norma, se denominan colectivamente conjeturas de Macdonald en este contexto: además de la fórmula de la norma, Macdonald conjeturó una fórmula para el valor de P_λ en el punto t^ρ, y una simetría

${\frac {P_{\lambda }(\dots ,q^{\mu _{i}}t^{\rho _{i}},\dots )}{P_{\lambda }(t^{\rho })}}={\frac {P_{\mu }(\dots ,q^{\lambda _{i}}t^{\rho _{i}},\dots )}{P_{\mu }(t^{\rho })}}.$

Nuevamente, fueron probadas para sistemas de raíces reducidos generales por (Cherednik, 1995), usando álgebras de Hecke doblemente afines, y la extensión al caso BC siguió poco después a través del trabajo de van Diejen, Noumi y Sahi.

Conjetura de positividad de Macdonald

En el caso de sistemas de raíces del tipo A_n−1 los polinomios de Macdonald son simplemente polinomios simétricos en n variables con coeficientes que son funciones racionales de q y t. Cierta versión transformada ${\widetilde {H}}_{\mu }$ de los polinomios de Macdonald (véase la fórmula combinatoria a continuación) forma una base ortogonal del espacio de funciones simétricas sobre $\mathbb {Q} (q,t)$ y, por lo tanto, se puede expresar en términos de funciones de Schur $s_{\lambda }$. Los coeficientes K_λμ(q,t) de estas relaciones se denominan coeficientes de Kostka–Macdonald o coeficientes qt-Kostka.

Macdonald conjeturó que los coeficientes de Kostka y Macdonald eran polinomios en q y t con coeficientes enteros no negativos. Estas conjeturas están ahora probadas; el paso más difícil y final fue probar la positividad, lo que hizo Mark Haiman (2001), al probar la conjetura n!.

Todavía es un problema central abierto en la combinatoria algebraica encontrar una fórmula combinatoria para los coeficientes qt-Kostka.

Conjetura n!

La conjetura n! de Adriano Garsia y Mark Haiman establece que para cada partición μ de n, el espacio

$D_{\mu }=C[\partial x,\partial y]\,\Delta _{\mu }$

abarcado por todas las derivadas parciales superiores de

$\Delta _{\mu }=\det(x_{i}^{p_{j}}y_{i}^{q_{j}})_{1\leq i,j,\leq n}$

tiene dimensión n!, donde (p_j, q_j) recorre los n elementos del diagrama de la partición μ, considerado como un subconjunto de los pares de enteros no negativos. Por ejemplo, si μ es la partición 3 = 2 + 1 de n = 3 entonces los pares (p_j, q_j) son (0, 0), (0, 1), (1, 0), y el espacio D_μ está dividido por

$\Delta _{\mu }=x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}$

$y_{2}-y_{3}$

$y_{3}-y_{1}$

$x_{3}-x_{2}$

$x_{1}-x_{3}$

$1$

que tiene dimensión 6 = 3!.

¡La prueba de Haiman de la conjetura de positividad de Macdonald y la conjetura n! implicaba mostrar que el esquema de Hilbert isoespectral de n puntos en un plano era de Cohen–Macaulay (e incluso de Gorenstein). Los resultados anteriores de Haiman y Garsia ya habían demostrado que esto implicaba la conjetura n!, y que la conjetura n! implicaba que los coeficientes de Kostka–Macdonald eran multiplicidades de caracteres graduadas para los módulos D_μ. Esto implica inmediatamente la conjetura de positividad de Macdonald porque las multiplicidades de caracteres tienen que ser números enteros no negativos.

Ian Grojnowski y Mark Haiman encontraron otra prueba de la conjetura de positividad de Macdonald al demostrar una conjetura de positividad para el polinomio LLT.

Fórmula combinatoria para los polinomios de Macdonald

En 2005, J. Haglund, M. Haiman y N. Loehr​ dieron la primera prueba de una interpretación combinatoria de los polinomios de Macdonald. En 1988, I. G. Macdonald​ dio la segunda prueba de una interpretación combinatoria de los polinomios de Macdonald (ecuaciones (4.11) y (5.13)).

La fórmula de Macdonald es diferente a la del trabajo de Haglund, Haiman y Loehr, con muchos menos términos (esta fórmula también se demuestra en el trabajo seminal de Macdonald,​ Ch. VI (7.13)). Si bien es muy útil para el cálculo e interesante por derecho propio, sus fórmulas combinatorias no implican inmediatamente la positividad de los coeficientes $K_{\lambda \mu }(q,t),$ de Kostka-Macdonald, ya que dan la descomposición de los polinomios de Macdonald en funciones simétricas monomiales en lugar de con funciones de Schur.

Escritos en los polinomios de Macdonald transformados ${\widetilde {H}}_{\mu }$ en lugar de los habituales $P_{\lambda }$, son

${\widetilde {H}}_{\mu }(x;q,t)=\sum _{\sigma :\mu \to \mathbb {Z} _{+}}q^{inv(\sigma )}t^{maj(\sigma )}x^{\sigma }$

donde σ es un relleno del diagrama de Young de forma μ, inv y maj son ciertas estadísticas combinatorias (funciones) definidas en el relleno σ. Esta fórmula expresa los polinomios de Macdonald en infinitas variables. Para obtener los polinomios en n variables, basta con restringir la fórmula a rellenos que solo usen los números enteros 1, 2, ..., n. El término x^σ debe interpretarse como $x_{1}^{\sigma _{1}}x_{2}^{\sigma _{2}}\cdots$ donde σ_i es el número de casillas en el relleno de μ con contenido i.

Esto representa el brazo y la pierna de un cuadrado de un diagrama de Young. El brazo (a, de arm) es el número de cuadrados a su derecha, y la pierna (l, de leg) es el número de cuadrados situados por encima

Los polinomios de Macdonald transformados ${\widetilde {H}}_{\mu }(x;q,t)$ en la fórmula anterior están relacionados con los polinomios de Macdonald clásicos $P_{\lambda }$ a través de una secuencia de

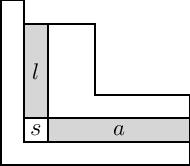
transformaciones. Primero, la forma integral de los polinomios de Macdonald, denominada $J_{\lambda }(x;q,t)$, es una nueva escala de $P_{\lambda }(x;q,t)$ que permite eliminar los denominadores de los coeficientes:

$J_{\lambda }(x;q,t)=\prod _{s\in D(\lambda )}(1-q^{a(s)}t^{1+l(s)})\cdot P_{\lambda }(x;q,t)$

donde $D(\lambda )$ es la colección de cuadrados en el diagrama de Young de $\lambda$, y $a(s)$ y $l(s)$ denotan el brazo y la pierna del cuadrado $s$, como se muestra en la figura. Nota: la figura de la derecha usa la notación francesa para el cuadro, que se invierte verticalmente de la notación inglesa que se usa en la página de Wikipedia para los diagramas de Young. La notación francesa se usa más comúnmente en el estudio de los polinomios de Macdonald.

Los polinomios de Macdonald transformados ${\widetilde {H}}_{\mu }(x;q,t)$ se pueden definir en términos de los $J_{\mu }$. Se tiene que

${\widetilde {H}}_{\mu }(x;q,t)=t^{-n(\mu )}J_{\mu }\left[{\frac {X}{1-t^{-1}}};q,t^{-1}\right]$

donde

$n(\mu )=\sum _{i}\mu _{i}\cdot (i-1).$

La notación de paréntesis anterior denota la sustitución pletística.

Esta fórmula se puede usar para probar la fórmula de Knop y Sahi para los polinomios de Jack.

Polinomios de Macdonald no simétricos

En 1995, Macdonald introdujo un análogo no simétrico de los polinomios simétricos de Macdonald. Los polinomios de Macdonald simétricos se pueden recuperar fácilmente de la contraparte no simétrica. En su definición original, muestra que los polinomios de Macdonald no simétricos son una familia única de polinomios ortogonales con respecto a un cierto producto interno, así como satisfacer una propiedad de triangularidad cuando se expande en la base del monomio.

En 2007, Haglund, Haiman y Loehr dieron una fórmula combinatoria para los polinomios de Macdonald no simétricos.

Los polinomios no simétricos de Macdonald se especializan en caracteres de Demazure, tomando q=t=0, y a clave de polinomios cuando q=t=∞.

Fórmulas combinatorias basadas en el proceso de exclusión

En 2018, S. Corteel, O. Mandelshtam y L. Williams utilizaron el proceso de exclusión para brindar una caracterización combinatoria directa de los polinomios de Macdonald simétricos y no simétricos.​ Sus resultados difieren del trabajo anterior de Haglund en parte porque dan una fórmula directamente para los polinomios de Macdonald en lugar de una transformación de los mismos. Desarrollan el concepto de una cola multilíneal, que es una matriz que contiene bolas o celdas vacías junto con una aplicación entre las bolas y sus vecinas y un mecanismo de etiquetado combinatorio. El polinomio de Macdonald no simétrico entonces satisface:

$E_{\lambda }({\textbf {x}};q,t)=\sum _{Q}\mathrm {wt} (Q)$

donde la suma es sobre todas las colas multilíneales $L\times n$ de tipo $\lambda$ y $\mathrm {wt}$ es una función de ponderación que asigna esas colas a polinomios específicos. El polinomio simétrico de Macdonald satisface:

$P_{\lambda }({\textbf {x}};q,t)=\sum _{\mu }E_{\mu }(x_{1},...,x_{n};q,t)=\sum _{\mu }\sum _{Q}\mathrm {wt} (Q)$

donde la suma exterior se aplica sobre todas las composiciones distintas $\mu$ que son permutaciones de $\lambda$, y la suma interior es como antes.

Bibliografía

• Cherednik, Ivan (1995), «Double Affine Hecke Algebras and Macdonald's Conjectures», Annals of Mathematics, Second Series (Annals of Mathematics) 141 (1): 191-216, ISSN 0003-486X, JSTOR 2118632, doi:10.2307/2118632 .
• Garsia, Adriano; Remmel, Jeffrey B. (15 de marzo de 2005), «Breakthroughs in the theory of Macdonald polynomials», PNAS 102 (11): 3891-3894, Bibcode:2005PNAS..102.3891G, PMC 554818, PMID 15753285, doi:10.1073/pnas.0409705102 .
• Mark Haiman Combinatoria, funciones simétricas y esquemas de Hilbert Desarrollos actuales en matemáticas 2002, no. 1 (2002), 39-111.
• Haiman, Mark Notas sobre los polinomios de Macdonald y la geometría de los esquemas de Hilbert. Funciones simétricas 2001: encuestas de desarrollos y perspectivas, 1–64, NATO Sci. Ser. II Matemáticas. física Chem., 74, Kluwer Acad. Publ., Dordrecht, 2002. MR 2059359
• Haiman, Mark (2001), «Hilbert schemes, polygraphs, and the Macdonald positivity conjecture», J. Amer. Math. Soc. 14 (4): 941-1006, S2CID 9253880, arXiv:math.AG/0010246, doi:10.1090/S0894-0347-01-00373-3 .
• Kirillov, A. A. (1997), «Lectures on affine Hecke algebras and Macdonald's conjectures», Bull. Amer. Math. Soc. 34 (3): 251-292, doi:10.1090/S0273-0979-97-00727-1 .
• Macdonald, I. G. (1982), «Some conjectures for root systems», SIAM Journal on Mathematical Analysis 13 (6): 988-1007, ISSN 0036-1410, MR 674768, doi:10.1137/0513070 .
• Macdonald, I. G. "Funciones simétricas y polinomios de Hall". Segunda edición. Monografías matemáticas de Oxford. Publicaciones científicas de Oxford. The Clarendon Press, Oxford University Press, Nueva York, 1995. x+475 págs. ISBN 0-19-853489-2 MR 1354144
• Macdonald, I. G. "Funciones simétricas y polinomios ortogonales". Conferencias en memoria de Dean Jacqueline B. Lewis presentadas en la Universidad de Rutgers, New Brunswick, NJ. University Lecture Series, 12. American Mathematical Society, Providence, RI, 1998. xvi+53 pp. ISBN 0-8218-0770-6 MR 1488699
• Macdonald, I. G. "Álgebras afines de Hecke y polinomios ortogonales". Séminaire Bourbaki 797 (1995).
• Macdonald, I. G. (2000–2001), «Orthogonal polynomials associated with root systems», Séminaire Lotharingien de Combinatoire 45: Art. B45a, MR 1817334, arXiv:math.QA/0011046 .
• Macdonald, I. G. (2003), Affine Hecke algebras and orthogonal polynomials, Cambridge Tracts in Mathematics 157, Cambridge: Cambridge University Press, pp. x+175, ISBN 978-0-521-82472-9, MR 1976581 .

Enlaces externos

• Página de Mike Zabrocki sobre polinomios de Macdonald.
• Algunos de artículos de Haiman sobre los polinomios de Macdonald.

• Datos: Q17098676