Módulo inyectivo

En matemáticas, un módulo inyectivo es un módulo Q que comparte ciertas propiedades deseables con el Z-módulo Q de todos los números racionales. Específicamente, si Q es un submódulo de algún otro módulo, entonces es un sumando directo de ese módulo; también, dado un submódulo de un módulo Y, entonces cualquier homomorfismo de módulos de este submódulo a Q se puede ampliar a un homomorfismo de todo Y a Q. Este concepto es dual al de los módulos proyectivos.

Definición[editar]

Más formalmente, un módulo izquierdo Q sobre el anillo R es inyectivo si satisface una de (y por lo tanto todas) las condiciones equivalentes siguientes:

Si Q es un submódulo de un otro R-módulo izquierdo M, entonces existe otro submódulo K de M tal que M es la suma directa interna de Q y de K, es decir, Q +K=M y Q ∩ K = {0}.

Si X es un submódulo del R- módulo izquierdo Y y g: X → Q es un homomorfismo de módulos, entonces existe un homomorfismo de módulos h: Y → Q tal que h(x) = g(x) para todo x en X.

Si X y Y son R-módulos izquierdos y f: X → Y es un homomorfismo inyectivo de módulos y g: X → Q es un homomorfismo de módulos arbitrario, entonces existe un homomorfismo de módulos h: Y → Q tal que hf = g, es decir tal que el diagrama siguiente conmuta:

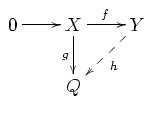
Cualquier sucesión exacta corta 0 → Q → M → K → 0 de R-módulos izquierdos, se escinde.

El funtor contravariante Hom(-, Q) de la categoría de los R- módulos izquierdos a la categoría de grupos abelianos es exacto.

los R-módulos derechos inyectivos se definen análogamente.

Ejemplos[editar]

Trivialmente, el módulo cero {0} es inyectivo.

Cada espacio vectorial Q es inyectivo. Razón: si Q es un subespacio de V, podemos encontrar una base de Q y ampliarla a una base de V. Los nuevos vectores de base extienden un subespacio K de V y V es la suma directa interna de Q y de K. Observe que el complemento directo K de Q no es determinado unívocamente por Q, y la función g que extiende en la definición anterior no es única, típicamente.

Si G es un grupo finito y k un cuerpo de característica 0, entonces se muestra en la teoría de representaciones de grupo que cualquier subrepresentación de la dada es ya un sumando directo de la dada. Traducido a lenguaje de módulos, esto significa que todos los módulos sobre el álgebra de grupo k[G] son inyectivos. Pero si la característica de k no es cero, el ejemplo siguiente puede ayudar: Si A es una álgebra asociativa unital sobre el cuerpo k con dimensión finita sobre k, entonces Hom_k(-, k) es una dualidad entre los A-módulos a la izquierda finitamente generados y los A-módulos a la derecha finitamente generados. Por lo tanto, los A-módulos a la izquierda finitamente generados son exactamente los módulos de la forma Hom_k(P, k) donde P es un A-módulo a la derecha finitamente generado proyectivo.

Sobre otros anillos, los módulos inyectivos son abundantes, pero no es fácil ejemplificar sin una cierta teoría (mencionada abajo). Los números racionales Q (con la adición) forman un grupo abeliano inyectivo (es decir un Z-módulo inyectivo). El grupo cíclico Z/n Z para n > 1 es inyectivo como Z/n Z - módulo, pero no es inyectivo como grupo abeliano.

Hechos[editar]

Cualquier producto (incluso infinitamente muchos) de módulos inyectivos es inyectivo. Cada suma directa finita de módulos inyectivos es inyectiva. En general, los submódulos, los módulos factor o las sumas directas infinitas de módulos inyectivos no necesitan ser inyectivos.

Para demostrar que un módulo dado es inyectivo, el siguiente lema de prueba de inyectividad es útil: un R-módulo izquierdo Q es inyectivo si y solamente si cualquier homomorfismo g: I → Q definido en un ideal a izquierda I de R se puede extender a todo R. Usando este criterio, se puede demostrar que Q es un grupo abeliano inyectivo (es decir un Z-módulo inyectivo).

Más generalmente, un grupo abeliano es inyectivo si y solamente si es un Z-módulo divisible. Más generalmente aún: un módulo sobre un dominio de ideales principales es inyectivo si y solamente si es divisible. Uno puede ver el ejemplo sobre espacios vectoriales como caso especial de este teorema, pues cada espacio vectorial es divisible.

El módulo inyectivo más importante es quizá el grupo abeliano Q/Z. Es un cogenerator inyectivo en la categoría de grupos abelianos, que significa que es inyectivo y cualquier otro módulo está contenido en un producto convenientemente grande de copias de Q/Z. En particular, cada grupo abeliano es subgrupo de un inyectivo. Es muy significativo que esto sea también verdad sobre cualquier anillo: cada módulo es submódulo de un inyectivo, o "la categoría de R-módulos izquierdos tiene bastante inyectivos." Para probar esto, uno utiliza las propiedades peculiares del grupo abeliano Q/Z para construir un cogenerator inyectivo en la categoría de R- módulos izquierdos. Se puede entonces definir la clausura inyectiva de un módulo (esencialmente el módulo inyectivo más pequeño que contiene al dado).

Cada módulo M también tiene una resolución inyectiva: una sucesión exacta de la forma

0 → M → I ⁰ → I ¹ → I² → ...

donde I^j es inyectivo. Se utilizan estas resoluciones inyectivas para definir la dimensión inyectiva de un módulo (la longitud de la resolución inyectiva más corta que termina en ceros, si existe una resolución finita) así como funtores derivados.

Cada módulo inyectivo indescomponible tiene un anillo de endomorfismos local.

Generalización[editar]

Uno también habla de objetos inyectivos en categorías más generales que las categorías de módulos, por ejemplo en categorías de funtores o en categorías de haces de O_X módulos sobre un cierto espacio anillado (X, O_X). Se utiliza la definición general siguiente: un objeto Q en la categoría C es inyectivo si para cualquier monomorfismo f: X → Y en C y cualquier morfismo g: X → Q existe un morfismo h: Y → Q con hf = g.

Referencias[editar]

F.W. Anderson and K.R. Fuller: Rings and Categories of Modules, Graduate Texts in Mathematics, Vol. 13, 2nd Ed., Springer-Verlag, New York, 1992.

Datos: Q2716519