Motor Stirling
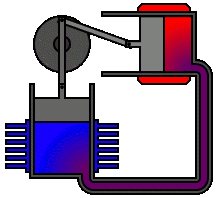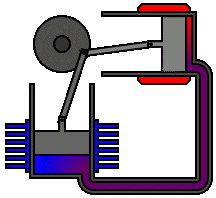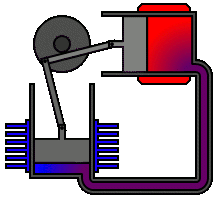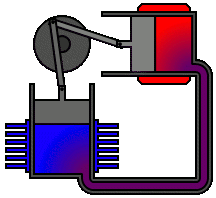


Un motor Stirling es un motor térmico que opera por compresión y expansión cíclica de aire u otro gas (el llamado fluido de trabajo) a diferentes niveles de temperatura que producen una conversión neta de energía calorífica a energía mecánica.[1][2] Más específicamente, es un motor térmico de ciclo cerrado regenerativo con un fluido gaseoso permanente. En esta definición, ciclo cerrado describe un sistema termodinámico en el que el fluido está permanentemente contenido en el sistema, y regenerativo describe el uso de un tipo específico de intercambio de calor y almacenamiento térmico, conocido como el regenerador. La inclusión de un regenerador es lo que diferencia a los motores Stirling de otros motores de ciclo cerrado.
El motor Stirling fue inventado en 1816[3] por el reverendo escocés Robert Stirling, quien lo concibió para rivalizar con el motor de vapor. En la práctica, su uso se redujo a aplicaciones domésticas durante casi un siglo.[4] El motor Stirling se hizo famoso en 1842 cuando Stirling construyó una máquina con este diseño en Dundee, con una potencia de 37 caballos.[5] Los motores Stirling tienen una alta eficiencia, si se los compara con los motores de vapor,[6] y gran facilidad para ser aplicados a cualquier fuente de calor. Estas ventajas están haciendo que vuelva a haber interés este tipo de motores, y en su aplicación a sistemas captadores de energías renovables.
Historia[editar]
Robert Stirling es considerado el inventor del motor de aire caliente, a pesar de algunos predecesores anteriores, especialmente Guillaume Amontons.[7] Logró construir, en 1816, el primer motor de aire caliente en funcionamiento.

Más tarde lo siguió Cayley. Este tipo de motor era de aquellos en los que el fuego está cerrado y alimentado por aire bombeado debajo de la rejilla en cantidad suficiente para mantener la combustión, mientras que la mayor parte del aire entra por encima del fuego para calentarse y expandirse; el todo, junto con los productos de la combustión, luego actúa sobre el pistón y pasa a través del cilindro de trabajo; y la operación es solo de mezcla simple, no se requiere una superficie de calentamiento de metal, el aire a calentar se pone en contacto inmediato con el fuego.
El principio del motor de aire Stirling difiere del de Sir George Cayley (1807), en el que el aire es forzado a través del horno y se expulsa, mientras que en el motor de Stirling el aire funciona en un circuito cerrado. Fue a eso que el inventor dedicó la mayor parte de su atención. Un motor de dos caballos de fuerza, construido en 1818 para bombear agua en una cantera de Ayrshire (Escocia), continuó funcionando durante algún tiempo, hasta que un asistente descuidado permitió que el calentador se sobrecalentara. Este experimento demostró al inventor que, debido a la baja presión de trabajo obtenible, el motor solo podía adaptarse a pequeñas potencias para las que en ese momento no había demanda.
La patente de Stirling 1816 también se refería a un "Economizador", que es el predecesor del regenerador. En esta patente (# 4081) describe la tecnología "economizadora" y varias aplicaciones donde se puede usar dicha tecnología. De ellos surgió un nuevo arreglo para un motor de aire caliente. En 1818, se construyó un motor para bombear agua de una cantera en Ayrshire, pero debido a problemas técnicos, el motor fue abandonado por un tiempo.
Stirling patentó un segundo motor de aire caliente, junto con su hermano James, en 1827. Invirtieron el diseño para que los extremos calientes de los desplazadores estuvieran debajo de la maquinaria y agregaron una bomba de aire comprimido para que el aire dentro pudiera aumentar la presión a alrededor de 20 atmósferas.
Los dos hermanos Stirling fueron seguidos poco después (1828) por Parkinson y Crossley y Arnott en 1829.
Estos precursores, a los que debe añadirse Ericsson, han traído al mundo la tecnología del motor de aire caliente y sus enormes ventajas sobre la máquina de vapor. Cada uno de ellos venía con su propia tecnología específica, y aunque el motor Stirling y los motores Parkinson y Crossley eran bastante similares, Robert Stirling se distinguió al inventar el regenerador.
Parkinson y Crosley introdujeron el principio de usar aire de mayor densidad que el de la atmósfera, y así obtuvieron un motor de mayor potencia en la misma brújula. James Stirling siguió esta misma idea cuando construyó el famoso motor Dundee.
La patente de Stirling de 1827 fue la base de la tercera patente de Stirling de 1840. Los cambios de la patente de 1827 fueron menores pero esenciales, y esta tercera patente condujo al motor Dundee.
James Stirling presentó su motor a la Institución de Ingenieros Civiles en 1845.[8] El primer motor de este tipo que, después de varias modificaciones, fue construido y calentado eficientemente, tenía un cilindro de 30 centímetros de diámetro, con una longitud de carrera de 60 centímetros, e hizo 40 revoluciones en un minuto (40 rpm). Este motor movió toda la maquinaria en las obras de Dundee Foundry Company durante ocho o diez meses, y anteriormente se descubrió que era capaz de elevar 320,000 kg 60 cm en un minuto, una potencia de aproximadamente 21 caballos de fuerza.
Al encontrar esta potencia insuficiente para sus trabajos, la Dundee Foundry Company erigió el segundo motor, con un cilindro de 40 centímetros de diámetro, una carrera de 1,2 metros y haciendo 28 turnos en un minuto. Cuando este motor había estado en funcionamiento continuo durante más de dos años, no solo había realizado el trabajo de la fundición de la manera más satisfactoria, sino que había sido probado (por un freno de fricción en un tercer motor) hasta el punto de levantar casi 687 toneladas, una potencia de aproximadamente 45 caballos de fuerza.
Esto da un consumo de 1.2 kilogramos por caballo de fuerza por hora; pero cuando el motor no estaba totalmente cargado, el consumo era considerablemente inferior a 1.1 kilogramos por caballo de fuerza por hora. Este rendimiento estuvo al nivel de las mejores máquinas de vapor, cuya eficiencia fue de alrededor del 10%. Después de James Stirling, tal eficiencia solo fue posible gracias al uso del economizador (o regenerador).
Descripción del funcionamiento[editar]
El motor Stirling es el único capaz de aproximarse (teóricamente lo alcanza) al rendimiento máximo teórico conocido como rendimiento de Carnot, por lo que, en lo que a rendimiento de motores térmicos se refiere, es la mejor opción. Conviene advertir que no serviría como motor de coche, porque aunque su rendimiento es superior, su potencia es inferior (a igualdad de peso) y el rendimiento óptimo solo se alcanza a velocidades bajas. El ciclo teórico de Carnot es inalcanzable en la práctica, y el ciclo Stirling real tendría un rendimiento intrínsecamente inferior al Ciclo de Carnot, además el rendimiento del ciclo es sensible a la temperatura exterior, por lo que su eficiencia es mayor en climas fríos como el invierno en los países nórdicos, mientras tendría menos interés en climas como los de los países ecuatoriales, conservando siempre la ventaja de los motores de combustión externa de las mínimas emisiones de gases contaminantes, y la posibilidad de aceptar fuentes de calor sin combustión.
Su ciclo de trabajo se conforma mediante 2 transformaciones isocóricas (calentamiento y enfriamiento a volumen constante) y dos isotermas (compresión y expansión a temperatura constante).[9][10]
Existe un elemento adicional al motor, llamado regenerador, que, aunque no es indispensable, permite alcanzar mayores rendimientos. El regenerador es un intercambiador de calor interno que tiene la función de absorber y ceder calor en las evoluciones a volumen constante del ciclo. El regenerador consiste en un medio poroso con conductividad térmica despreciable, que contiene un fluido. El regenerador divide al motor en dos zonas: una zona caliente y otra zona fría. El fluido se desplaza de la zona caliente a la fría durante los diversos ciclos de trabajo, atravesando el regenerador.
Puede emplear 1, 2, 3 o más pistones.
Rendimiento del ciclo[editar]
La definición de rendimiento para una máquina térmica es:
El trabajo neto será el debido a la expansión y compresión isotérmicas, puesto que durante los procesos isocóricos no se realiza trabajo. Para un gas ideal se calcula como
| Símbolo | Nombre |
|---|---|
| Vmin | Volumen mínimo |
| Vmax | Volumen máximo |
| TC | Temperatura de fuente caliente |
| TF | Temperatura de fuente fría |
| r | Relación de compresión |
Definiendo la relación de compresión como y aplicando propiedades del logaritmo, se reduce a
.
El gas solo absorbe calor durante dos etapas: el calentamiento a volumen constante y la expansión isotérmica. Para un gas ideal esto representa
.
En la práctica es común el uso de regeneradores, que permiten almacenar el calor cedido por el gas durante el enfriamiento a volumen constante para luego devolverlo al sistema durante el proceso de calentamiento. Si bien ambas cantidades son iguales en módulo, puesto que se tratan de procesos isocóricos entre las mismas dos temperaturas, el regenerador no es perfecto y parte de esa energía se pierde. Definiendo su eficiencia como , se obtiene
.
Finalmente el rendimiento total de la máquina resulta
.
En la medida que el funcionamiento del regenerador se acerca al caso ideal, el rendimiento del ciclo se aproxima al del ciclo de Carnot
.
Aplicaciones[editar]
En España, en la Plataforma Solar de Almería, se han construido equipos (conocidos como Distal y EuroDISH) formados por grandes discos parabólicos que reflejan y concentran la luz solar hacia un motor Stirling, el cual produce energía mecánica que mediante un alternador es transformada en energía eléctrica. Son modelos experimentales y demostrativos de gran rendimiento.
Esta tecnología se considera que será de gran aplicación para regiones donde hay gran número de pobladores dispersos, a los cuales sería muy costoso llegar con red eléctrica.
Es de esperar que los fabricantes de motores Stirling construyan en gran escala unidades pequeñas de ese mismo tipo, (con disco solar) como por ejemplo con capacidad de producir unos 200 a 400 kWh al mes (equipos de 1 a 2 kW de potencia aproximadamente); especialmente para los países situados entre los trópicos, pues en estas zonas la cantidad de radiación solar es grande a lo largo de todo el año y a su vez es la región donde hay más población dispersa.
Industria espacial y otras[editar]
La Agencia Espacial Norteamericana desarrolló unos generadores con radioisótopos Stirling (SRG), basado en un motor Stirling cuya unidad de calentamiento es a base de radioisótopos. El extremo caliente alcanza altas temperaturas y el helio calentado impulsa el pistón, cuyo movimiento se convierte en electricidad, disipando el calor en el extremo frío del motor. Mediante pistones y rodamientos de levitación magnética, se logra una alta eficiencia y larga duración del generador, llegando a lograrse 14 años de funcionamiento continuo sin mantenimiento.[11]
Dado el suministro muy limitado de plutonio, el convertidor Stirling es notable por producir aproximadamente cuatro veces más energía eléctrica en comparación con un generador termoeléctrico de radioisótopos (RTG). La NASA probó exhaustivamente los generadores Stirling en la Tierra, pero su desarrollo se canceló en 2013 antes de que pudieran desplegarse en misiones de naves espaciales reales. Un proyecto similar de la NASA aún en desarrollo a partir del 21 de abril de 2020, llamado Kilopower, también utiliza motores Stirling, pero utiliza un pequeño reactor de fisión de uranio como fuente de calor.
En Holanda, SoundEnergy, una startup neerlandesa, convierte el calor en frío a través de un motor Stirling. Se basa en principios bien entendidos de la termoacústica y fue investigado originalmente por el Departamento de Defensa de los Estados Unidos, según asegura la compañía.[12]
Referencias[editar]
- ↑ "Stirling Engines", G. Walker (1980), Clarendon Press, Oxford, page 1: "A Stirling engine is a mechanical device which operates on a *closed* regenerative thermodynamic cycle, with cyclic compression and expansion of the working fluid at different temperature levels."
- ↑ W.R. Martini (1983), p.6
- ↑ «El motor Stirling de 1816». hotairengines.org.
- ↑ T. Finkelstein; A.J. Organ (2001), Chapters 2&3
- ↑ «El motor Stirling de Dundee». hotairengines.org.
- ↑ Stirling engines capable of reaching 40% efficiency
- ↑ «El motor de Amontons». hotairengines.org.
- ↑ «Dundee Stirling Engine - Lecture». hotairengines.org.
- ↑ A. Romanelli Alternative thermodynamic cycle for the Stirling machine, American Journal of Physics 85, 926 (2017)
- ↑ A. Romanelli Stirling engine operating at low temperature difference , American Journal of Physics 88, 319 (2020); https://doi.org/10.1119/10.0000832
- ↑ «Stirling Convertor sets 14-year continuous operation milestone». Space Daily. Consultado el 21 de abril de 2020.
- ↑ «Una startup holandesa convierte el calor en frío a través de un motor Stirling, una solución que no requiere energía». Consultado el 21 de abril de 2020.









![{\displaystyle \eta \ {\xrightarrow[{\eta _{R}\rightarrow 1}]{}}\left(1-{\frac {T_{F}}{T_{C}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cdf1954d5fdb92d26993a3d5fbec10f1bfb1e55)