Modelo de agua subterránea

De Wikipedia, la enciclopedia libre
(Redirigido desde «Modelaje de acuíferos»)
Fig.1. Factores hídricos que influyen el agua subterránea

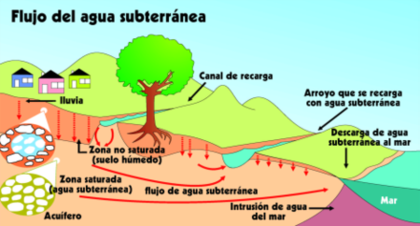
Un modelo de agua subterránea o modelado de acuíferos es una técnica utilizada desde hace algunas décadas para el estudio del potencial de los acuíferos y para analizar el comportamiento de éstos a lo largo del tiempo, cuando son explotados por pozos, o se someten a procesos de recarga artificial.[1]​ Puede ser un modelo a escala o un modelo analógico, por ejemplo un modelo eléctrico basado en la analogía matemática entre el flujo de agua (ley de Darcy) y el flujo de electricidad (ley de Ohm). Sin embargo, en general, un modelo de agua subterránea se refiere a un modelo de computadora del flujo agua subterránea en sistemas acuíferos usados en la hidrogeología. El modelo puede incluir los aspectos químicos de la calidad del agua subterránea.

Los modelos de agua subterránea se emplean a menudo para predecir los efectos de cambios hidrológicos, sean naturales o artificiales, en el comportamiento de un acuífero. Se producen cambios artificiales, por ejemplo, por la extracción de agua para uso doméstico, industrial, y/o para regar. Estos modelos también son utilizados para predecir el efecto de la introducción del riego a base de un embalse o un bocatoma. Asimismo, los modelos se utilizan para evaluar los efectos de contaminación química en la superficie del suelo que pueda infiltrar en el acuífero bajo la influencia de la lluvia y lixiviación.

Los modelos han ido evolucionando rápidamente, en paralelo con la evolución de la capacidad de los ordenadores modernos y con los rápidos avances en el campo de los procedimientos de cálculo numérico. A lo largo de los años se han utilizado sucesivamente los modelos físicos, los modelos analógicos y recientemente han ocupado un espacio cada vez mayor los denominados modelos matemáticos.

Modelos físicos de acuíferos[editar]

Estos modelos reproducen en escala más reducida las situaciones que se verifican en la naturaleza, generalmente usando materiales semejantes. El ejemplo más obvio son los modelos construidos en arena de una parte o de todo el acuífero. El fluido utilizado en estos modelos puede ser el agua u otro líquido. Generalmente estos modelos son utilizados para efectos de demostración, son más útiles en situaciones en que el acuífero no está totalmente saturado, o para situaciones en que se analizan problemas con más de un fluido, como por ejemplo el estudio de la intrusión de agua salada en zonas costeras.

Con el paso del tiempo estos modelos han dejado de ser utilizados por las dificultades prácticas en su manejo; si la escala de los modelos es grande, es decir que el modelo es pequeño, en relación con el acuífero real, la importancia de otros fenómenos naturales, como por ejemplo la capilaridad, pasa a tener una preponderancia que no es real en la situación natural que se está simulando. Por otro lado si se utilizan escalas pequeñas, las dimensiones del modelo se hacen significativamente grandes y por lo tanto los costos se hacen prohibitivos.

Para la utilización de estos modelos se hace imprescindible contar con laboratorios hidráulicos bien equipados. Todo el proceso es bastante largo y costoso.

Modelos basados en técnicas analógicas[editar]

Las ecuaciones que representan el comportamiento de los acuíferos son muy semejantes a las que representan el comportamiento de los flujos eléctricos, a las que representan el flujo de fluidos entre placas paralelas, o las distribuciones de tensiones en membranas elásticas, por lo tanto se han utilizado en el pasado estas semejanzas (analogías) para resolver problemas de acuíferos.

Para la utilización de estos modelos también se hace imprescindible contar con laboratorios especializados.

Modelos con fluidos viscosos entre placas paralelas[editar]

El flujo de un fluido entre dos placas paralelas situadas a poca distancia una de la otra, generalmente conocido como "modelo de Hele-Shaw", puede ser utilizado para analizar varios tipos de problemas de acuíferos en dos dimensiones, o de fluidos múltiples. Las diferencias de permeabilidad de los acuíferos pueden ser simuladas por diferentes espaciamientos entre las placas paralelas.[2]​

Modelos de membranas[editar]

Si una membrana elástica es puesta en tensión, y con la punta de un lápiz ejercemos una presión sobre la misma, esta adquiere una forma muy semejante a la del cono de depresión que se produce en un acuífero homogéneo al extraerse agua desde un pozo. Se pueden calcular los factores que permiten traducir las depresiones de la membrana en las depresiones del acuífero.[3]​ Los modelos de membranas fueron útiles para determinar el nivel del agua en el acuífero en situaciones complejas de varios pozos y puntos de recarga. Sin embargo estos modelos solo son aplicables al estudio de situaciones estacionarias.

Modelos basados en la analogías eléctricas[editar]

Modelos de fluidos conductores[editar]

Utilizando un fluido conductor como por ejemplo el agua o un semifluido como una gelatina, sobre una base no conductora, la que puede ser fácilmente recreada para simular la forma del acuífero real, se puede determinar el comportamiento en la situación estacionaria del acuífero. Las diferencias de permeabilidad se pueden simular con la variación de la profundidad del fluido o del espesor de la gelatina conductora. Frecuentemente estos modelos se utilizaron para calibrar la permeabilidad del acuífero, con base en las profundidades del acuífero medidas en piezómetros en el campo, como paso previo a la construcción de los modelos con resistencias.

Modelos de papel conductor[editar]

Cuando la permeabilidad o la transmisibilidad es bastante homogénea, los problemas bidimensionales pueden ser fácilmente modelados con papel conductor, el que es cortado de acuerdo a la forma de los contornos del acuífero. Existen artificios, como por ejemplo modificar la escala del modelo para simular el aumento o disminución de la permeabilidad.[4]​

Este procedimiento puede ser utilizado también para determinar líneas de flujo y líneas equipotenciales en los cuerpos de los diques y en el suelo debajo de ellos.

Modelos de resistencias y condensadores[editar]

Este tipo de modelo analógico es el más citado en la bibliografía especializada, donde se describen con detalle interesantes aplicaciones.[5]​[6]​ En este tipo de modelos las resistencias simulan la transmisividad o permeabilidad del suelo, y los condensadores simulan la capacidad de almacenamiento del suelo. Muy frecuentemente son mencionados como "modelos R-C".

En los años 70, los computadores digitales disponían de programas de cálculo eficientes para la resolución de problemas de circuitos eléctricos complejos,[7]​ pero todavía no eran de dominio público los programas para la resolución de ecuaciones diferenciales por métodos numéricos, como por ejemplo el de las diferencias finitas. En esa época era bastante frecuente resolver los problemas de aguas subterráneas desarrollando un modelo análogo R-C, para luego resolverlo numéricamente a través de uno de los programas de computador accesibles en el mercado para resolver circuitos eléctricos.[6]​

Con la popularización de los programas de cómputo cada vez más genéricos que resuelven numéricamente las ecuaciones diferenciales, estos procedimientos complicados y rebuscados han quedado fuera de uso, yendo cada vez más hacia las soluciones totalmente numéricas.

Modelos basados en técnicas matemáticas[editar]

Es evidente que tanto los modelos físicos como los analógicos se basan en principios y ecuaciones matemáticos. Ya que los cálculos en el modelo matemático se basan en ecuaciones diferenciales que a menudo se dejan solucionar solamente por un análisis numérico, éstos modelos también se llaman modelos numéricos o modelos de simulación. [8]​ Existen varias técnicas de solución numérico como el método de diferencia finita o el método de los elementos finitos ambos requiriendo algún método iterativo. Actualmente las ecuaciones de flujo y de continuidad son resueltas con procedimientos matemáticos que suponen innecesaria la construcción de modelos materiales, sean físicos o analógicos. Los principales procedimientos para la resolución de estas ecuaciones pueden ser agrupadas en clásica (o analítica), soluciones a través del analizador diferencial, a través de procedimientos gráficas, a través de técnicas numéricas, a través del análisis del problema inverso.

Soluciones analíticas[editar]

Desafortunadamente las ecuaciones del flujo y de continuidad en su forma de ecuaciones diferenciales de derivadas parciales no tienen soluciones exacta cuando sus condiciones de contorno son complejas. Por otro lado generalmente los usuarios no disponen de un conocimiento suficiente de las matemáticas avanzadas para resolverlas. Sin embargo debe recordarse que este es el procedimiento ideal para la resolución de las ecuaciones. En los últimos decenios, sobre todo a partir de la década de 1970, los programas informáticos permiten la resolución de ecuaciones diferenciales con un conocimiento mínimo de los lenguajes de programación.

Cuando las condiciones de contorno son simplificadas, incluyendo las variaciones temporales, las ecuaciones pueden ser resueltas por este procedimiento.[9]​[10]​[11]​

Soluciones a través del analizador diferencial[editar]

El analizador diferencial es por definición un instrumento destinado a resolver ecuaciones diferenciales, pero no es apto para resolver ecuaciones de derivadas parciales, por lo tanto para utilizarlo en estos propósitos exige importantes simplificaciones que lo hacen poco atractivo como método general.

Soluciones gráficas[editar]

Para resolver problemas de situaciones transitorias donde la situación dominante es de tipo radial, como por ejemplo el producido por el bombeo desde un pozo, se pueden utilizar soluciones gráficas diseñando curvas típicas de succión por un pozo y superponiendo los efectos producidos por varios pozos, a lo largo del tiempo.[12]​[13]​ Básicamente se establece una retícula de puntos. Para cada uno de estos puntos se determina la acumulación de los efectos de las curvas tipo de vaciamiento del acuífero con base en las características de cada pozo en particular.

Soluciones a través de técnicas numéricas[editar]

Las técnicas numéricas incluyen procedimientos aritméticos que requieren el uso de ordenadores para efectuar los cálculos, dada la ingente cantidad de datos e iteraciones que deben efectuarse para llegar a soluciones estables. Si bien estos procedimientos también pueden ser resueltos manualmente requieren mucho tiempo, razón por la cual se desaconseja su aplicación manual.[14]​

En general para problemas de aguas subterráneas se utiliza el método de cálculo denominado de las diferencias finitas. Por este procedimiento se encuentra la situación de equilibrio para un instante de tiempo determinado, y se repite el procedimiento para sucesivos intervalos de tiempo. Si el intervalo de tiempo utilizado es suficientemente pequeño, se obtienen buenas aproximaciones. El método es descrito por Todd (1959) y Walton (1970).

Varios libros describen otros procedimientos numéricos señalando también las ventajas e inconvenientes de cada uno de ellos.[15]​[16]​

Datos de entrada[editar]

Fig. 2. Sección transversal de un acuífero semi-confinado y algunos datos de entrada

Para los cálculos se precisan datos de entrada como:

  • datos hidrológicos
  • datos de operación
  • datos de condiciones externos: condiciones iniciales y condiciones de límite
  • parámetros

El modelo puede tener componentes químicos como salinidad del agua o del suelo y otros indicadores de calidad química que también necesitan datos de entrada.

Datos hidrológicos[editar]

Factores hidrológicos a la superficie de suelo que determinan la recarga

Los datos hidrológicos de entrada pueden consistir de factores hidrológicos del balance hídrico como la precipitación, la lluvia, la evaporación, y la evapotranspiración que determinan la recarga del acuífero.
Estos datos pueden variar en el tiempo y de un lugar al otro.

Datos de operación[editar]

Los datos de operación se refieren a la intervención humana en el manejo de agua como el riego, el drenaje, la extracción de agua del acuífero mediante pozos, y su recarga artificial.
Estos datos pueden variar también en el tiempo y de un lugar al otro.

Muchos modelos hidrogeológicos sirven el propósito de evaluar los efectos de medidas de ingeniería hidráulica.

Fig. 3. Condiciones de límite

Condiciones iniciales y de límite[editar]

Las condiciones de límite se refieren por un lado a los niveles de la napa freática y presión artesiana a lo largo de los límites del área estudiada y, por otro lado, a los flujos de entrada y salida a lo largo de los límites. También pueden incluir los aspectos cualitativos del agua como la salinidad.

Las condiciones iniciales se refieren a los valores iniciales de elementos que, en el interior del modelo, pueden cambiar en el curso del tiempo y cubren mayormente los mismos elementos como las condiciones de límite.

Parámetros[editar]

Fig. 4. Ejemplo de parámetros de un modelo de riego combinado con un modelo de agua subterránea

Los parámetros se refieren a las propiedades físicos del acuífero que son constantes con el tiempo, pero que sí pueden variar de un sitio al otro.

Parámetros importantes son la topografía, la geometría y distancias, el espesor de las capas de suelo y la conductividad hidráulica (o permeabilidad, en el caso del agua), la transmisividad hidráulica, la resistencia hidráulica, la porosidad del suelo, el coeficiente de almacenamiento del suelo, y la capilaridad de la zona no saturada.

Algunos parámetros pueden ser influidos por cambios de la situación del agua subterránea, como el espesor de una capa del suelo, que puede disminuir cuando se baja el nivel freático. Este fenómeno se llama subsidencia. En este caso, el espesor no es un parámetro propio sino más bien un variable dependiente.

Dimensiones[editar]

Fig 5. Modelo 2-dimensional de drenaje subterráneo en un plano vertical
Fig. 6. Una red en tres dimensiones, ModFlow
Fig. 7 Plano de un modelo semi 3-dimensional radial con cilindros concéntricos por los cuales el flujo subterráneo pasa radialmente hacia el pozo

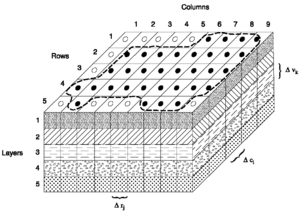
Modelos de agua subterránea pueden ser unidimensional, 2-dimensional, 3-dimensional y semi 3-dimensional. Los modelos de dos y tres dimensiones pueden tomar en cuenta que el suelo es anisotrópico en lo que se refiere a la conductividad hidráulica o permeabilidad para agua, es decir que esta propiedad difiere en las dos o tres direcciones.

1, 2 y 3-Dimensional[editar]

  1. Modelos unidimesionales se utilizan para flujo vertical en un sistema de capas de suelo paralelas horizontales aplicando la ley de Darcy.
  2. Modelos dos-dimensionales se aplican en planos verticales o horizontales asumiendo que las condiciones del agua subterránea se repiten en otros planos verticales respectivamente horizontales paralelos. Modelos de flujo hacia drenes en el drenaje subterráneo[17]​ de tierras agrícolas ofrecen ejemplos de modelos 2-dimensionales aplicados en planos verticales (fig. 5).
  3. Modelos tres-dimensionales como Modflow[18]​ requieren discretización de la región entera de flujo (fig. 6), que significa la subdivisión de la región en elementos 3-dimensionales más pequeños en el sentido vertical y horizontal ambos. Dentro de un elemento los valores de los parámetros se mantienen constantes, mientras entre los elementos puede haber variación. Utilizando soluciones numéricas de las ecuaciones de flujo subterráneo, la dirección del flujo puede ser horizontal - a cualquier ángulo con el norte - , vertical, y intermedio.

Semi 3-dimensional[editar]

En modelos semi 3-dimensionales el flujo horizontal se describe con ecuaciones de flujo 2-dimensional horizontal. Los flujos en sentido vertical, la tercera dirección, se describen (1) con una ecuación de flujo uni-dimensional vertical, o (2) se derivan de un balance hídrico de las recargas y descargas verticales, o (3) se derivan de un balance hídrico de flujos horizontales convirtiendo exceso de flujo horizontal entrando sobre flujo horizontal saliendo en un flujo vertical bajo la asunción que el agua es incompresible.

Hay dos clases de modelos semi tres-dimensionales:

  • modelos continuos o modelos radiales que consisten de modelos dos-dimensionales en planos radiales y verticales que se interceptan en un solo eje; el patrón del flujo se repite en cada plano radial vertical rodeando alrededor del eje; estos modelos no necesitan discretización.
  • modelos discretizados o modelos prismáticos que consisten de modelos formados por bloques verticales o prismas para el flujo horizontal combinado con un método de superposición del flujo vertical.
Fig. 8. Una red de dos dimensiones para un modelo semi 3-dimensional discretizado prismático sobre un cono aluvial, SahysMod

Modelo continuo radial[editar]

Un ejemplo de un modelo radial no-discretizado es la descripción del flujo subterráneo que mueve radialmente a un pozo profundo en un red de pozos de los cuales se abstraye agua.[19]​ El flujo radial pasa por una sección transversal vertical cilíndrico representando el equipotencial del cual la superficie se disminuye en la dirección del eje de intersección de los planos radiales donde el pozo está colocado (fig. 7).

Modelo discretizado prismático[editar]

En un modelo prismático como SahysMod[20]​ el flujo subterráneo entre las prismas colindantes (fig. 8) se describe con ecuaciones de flujo 2-dimensional horizontal. Los flujos verticales, en la tercera dirección, se describen con una ecuación de flujo uni-dimensional vertical, o se derivan de un balance hídrico de las recargas y descargas verticales, o de un balance hídrico de flujos horizontal convirtiendo exceso de flujo horizontal entrando sobre flujo horizontal saliendo en un flujo vertical bajo la asunción que el agua es incompresible.

Acuíferos semi-confinados con una capa poco permeable por encima de un acuífero artesiano en que el agua se encuentra bajo una presión mayor que la presión hidrostática pueden ser incluidos en el modelo semi 3-dimensional por simulación del flujo vertical bajo una sobre-presión con respecto al nivel freático.

Aplicabilidad[editar]

La aplicabilidad de un modelo de agua subterránea a una situación real depende de la conformidad del modelo con la realidad. También depende de la exactitud de los datos de entrada y de los parámetros. Su determinación pide un estudio considerable como la colección de los datos requeridos. Ya que muchos parámetros tienen bastante variación espacial, se necesita una opinión experta para llegar a valores representativos.

Análisis de sensibilidad[editar]

Los modelos pueden ser utilizados también para el análisis "si - entonces": si el valor de un parámetro is A, entonces que sería el resultado, y si el valor más bien es B, entonces que sería la influencia. Este análisis puede rendir una impresión aproximada del comportamiento del agua subterránea, pero también puede servir para hacer un análisis de sensibilidad que ayuda responder a la pregunta: ¿qué factores tienen influencia significante y cuales no? Can tal información se pueden restringir las investigaciones a los factores de mayor importancia.

Calibración[editar]

Cuando suficientes datos hayan sido recopilados, se pueden determinar algunos datos faltantes por el método de calibración, que implica que uno asume un rango de valores para el valor no conocido o dudoso de cierto parámetro ejecutando el programa del modelo repetidamente con los diferentes valores en el rango. Después uno compara los resultados de los variables dependientes obtenidos con los valores bien conocidos de datos correspondientes, se elige el valor en el rango que da el resultado más cercano, y entonces se asume que este es el valor verdadero. Por ejemplo, cuando datos de la salinidad del agua subterránea son disponibles y los valores de la conductividad hidráulica son inseguros, uno asume un rango de valores de conductividad y se selecciona el valor de conductividad como real que rinde una salinidad igual o casi igual al valor de salinidad medido. Esto significa que el flujo subterráneo, como gobernado por la conductividad hidráulica, concuerda con las condiciones de salinidad. Este procedimiento es semejante a la medición del flujo en un canal introduciendo agua muy salina por goteo y midiendo la concentración del flujo aguas abajo.

Véase también[editar]

Referencias[editar]

  1. ↑ R.G.Thomas. Groundwarwe models. Irrigation and Drainage paper N. 21. FAO. Roma. 1973
  2. ↑ Verruijt, A. Theory of groundwater flow. MacMillan & Co. - 1970.
  3. ↑ Todd,D.K. Groundwater hydrogeology, John Wiley & Sons. Inc. New York. 1959
  4. ↑ Davis, S.H. and de Wiest, R.J.M. Hydrogeology. John Wiley & Sons, Inc. New York. 1966.
  5. ↑ Walton C.W. Groundwater resource evaluation. McGraw Hill Book Company. 1970
  6. ↑ a b R.G.Thomas. Groundwater models. Irrigation and Drainage paper N. 21. FAO. Roma. 1973
  7. ↑ ECAP, ASTAP, SCEPTRE, por ejemplo
  8. ↑ Rushton, K.R., 2003, Groundwater Hydrology: Conceptual and Computational Models. John Wiley and Sons Ltd. ISBN 0-470-85004-3
  9. ↑ Verruijt, a. Theory of groundwater flow. MacMillan &Co. 1970
  10. ↑ Kruseman, G.P. ang de Ridder, N.A. Analysis and evaluation of pumping test data. Billetin N. 11. International Institute for Land Reclamation and Improvement. Wageningen,Netherlands. 1970
  11. ↑ Todd,D.K. Groudwater hydrogeology, John Wiley & Sons. Inc. New York. 1959
  12. ↑ Thomas, R.G. Grafical solution of groundwater flow problems pp. 50-69. Bulletin of the International Association of Scientific Hydrology, Vol.VI, N. 4 December 1961.
  13. ↑ Kruseman, G.P. ang de Ridder, N.A. Analysis and evaluation of pumping test data. Billetin N. 11. International Institute for Land Reclamation and Improvement. Wageningen,Netherlands. 1970
  14. ↑ Walton, C.W. Groundwater source evaluation. McGraw-Hill Book Company. 1970
  15. ↑ Remson, I., Hornberger, G.N, and Milz, F.J. Numerical method in subsurface hydrology with an introduction to the finite element method. 1971.
  16. ↑ Witherspoon, P.A., Javandel,I. and Neuman, S.P. Use of the finite element method in solving transient flow problem in aquifer systems. The use of analogue and digital computers in hydrology Vol II. IASH/Unesco Publ. N. 81
  17. ↑ The energy balance of groundwater flow applied to subsurface drainage in anisotropic soils by pipes or ditches with entrance resistance, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Bajar de: [1] o directamente como PDF : [2] Archivado el 19 de febrero de 2009 en Wayback Machine.
    Paper based on: R.J. Oosterbaan, J. Boonstra and K.V.G.K. Rao, 1996, The energy balance of groundwater flow. Published in V.P.Singh and B.Kumar (eds.), Subsurface-Water Hydrology, p. 153-160, Vol.2 of Proceedings of the International Conference on Hydrology and Water Resources, New Delhi, India, 1993. Kluwer Academic Publishers, Dordrecht, The Netherlands. ISBN 978-0-7923-3651-8. Bajar como PDF : [3] . El modelo se deja bajar de : [4]
  18. ↑ Online guide to MODFLOW-2000 and MODFLOW-2005
  19. ↑ Subsurface drainage by (tube)wells: well spacing equations for fully and partially penetrating wells in uniform or layered aquifers with or without anisotropy and entrance resistance. Paper explaining the basics of the WellDrain model, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Updated version of: R.J.Oosterbaan, Tube well spacing formulas for subsurface drainage. Published in: Smith, K.V.H. and D.W. Rycroft (eds.) Hydraulic Design in Water Resources Engineering: Land Drainage. Proceedings of the 2nd International Conference, Southampton University, p. 75‑84. Springer‑Verlag, Berlin, 1986. Bajar como PDF : [5] . El modelo se deja bajar de : [6]
  20. ↑ Ilri, 1995. SahysMod: Spatial Agro-Hydro-Salinity Model. Description of Principles, User Manual, and Case Studies International Institute for Land Reclamation and Improvement, Wageningen, Netherlands. Bajar como PDF : [7]

Software (enlaces externos)[editar]

Obtenido de «https://es.wikipedia.org/w/index.php?title=Modelo_de_agua_subterránea&oldid=156507450»