Fractura
La fractura es la separación de un objeto o material en dos o más piezas bajo la acción del estrés. La fractura de un sólido generalmente ocurre debido al desarrollo de ciertas superficies de discontinuidad de desplazamiento dentro del sólido. Si se desarrolla un desplazamiento perpendicular a la superficie de desplazamiento, se denomina grieta de tracción normal o simplemente una grieta; si un desplazamiento se desarrolla tangencialmente a la superficie de desplazamiento, se llama grieta de corte, banda de deslizamiento o dislocación.[1]
Las fracturas frágiles ocurren sin deformación aparente antes de la fractura; las fracturas dúctiles ocurren cuando la deformación visible ocurre antes de la separación. La resistencia a la fractura o la resistencia a la rotura es el estrés cuando una muestra falla o se fractura. Una comprensión detallada de cómo ocurre la fractura en los materiales puede ser asistida por el estudio de la mecánica de fractura.
Fuerza
[editar]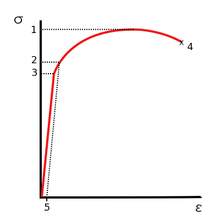
1) Resistencia a la tracción
2) Límite de elasticidad
3) Tensión límite proporcional
4) Fractura
5) Tensión de compensación (típicamente 0.2%)
La resistencia a la fractura, también conocida como resistencia a la rotura, es la tensión a la que falla una muestra por fractura.[2] Esto generalmente se determina para un espécimen dado mediante una prueba de tracción, que traza la curva de tensión-deformación (ver imagen). El punto final registrado es la resistencia a la fractura.
Los materiales dúctiles tienen una resistencia a la fractura inferior a la resistencia a la tracción final (UTS), mientras que en los materiales frágiles la resistencia a la fractura es equivalente a la UTS.[2] Si un material dúctil alcanza su máxima resistencia a la tracción en una situación de carga controlada,[Note 1] continuará deformando, sin aplicación de carga adicional, hasta que se rompa. Sin embargo, si la carga está controlada por desplazamiento,[Note 2] la deformación del material puede aliviar la carga, evitando la ruptura.
Tipos
[editar]Fractura por fragilidad
[editar]

En fracturas frágiles, no se produce deformación plástica aparente antes de la fractura. La fractura frágil generalmente implica poca absorción de energía y ocurre a altas velocidades, hasta 2 133.6 m/s (7 000 ft/s) en acero.[3] En la mayoría de los casos, la fractura frágil continuará incluso cuando se interrumpa la carga.[4]
En materiales cristalinos frágiles, la fractura puede ocurrir por escisión como resultado de la tensión de tracción que actúa de forma normal a planos cristalográficos con baja unión (planos de escisión). En los sólidos amorfos, por el contrario, la falta de una estructura cristalina da como resultado una fractura concoidea, con grietas que proceden de manera normal a la tensión aplicada.
La resistencia teórica de un material cristalino es (aproximadamente)
donde:
- es el módulo de Young del material,
- es la energía superficial, y
- es la distancia de equilibrio entre los centros atómicos.
Por otro lado, una grieta introduce una concentración de estrés modelada por
- (Para grietas afiladas)
donde:
- es el estrés de carga,
- es la mitad de la longitud de la grieta, y
- es el radio de curvatura en la punta de la grieta.
Al unir estas dos ecuaciones, obtenemos
Mirando de cerca, podemos ver grietas agudas (pequeñas ) y defectos grandes (grandes ) ambos disminuyen la resistencia a la fractura del material.
Los científicos han descubierto la fractura supersónica, el fenómeno de propagación de grietas más rápido que la velocidad del sonido en un material.[5] Este fenómeno también se verificó mediante un experimento de fractura en materiales similares al caucho.
La secuencia básica en una fractura frágil típica es: la introducción de una falla antes o después de que el material se ponga en servicio, la propagación lenta y estable de la grieta bajo carga recurrente, y la falla repentina y rápida cuando la grieta alcanza la longitud crítica de la grieta según las condiciones definidas por mecánica de fractura.[4] La fractura frágil se puede evitar controlando tres factores principales: la resistencia a la fractura del material (Kc), el nivel de tensión nominal (σ) y el tamaño del defecto introducido (a).[3] Las tensiones residuales, la temperatura, la velocidad de carga y las concentraciones de tensión también contribuyen a la fractura frágil al influir en los tres factores principales.
Bajo ciertas condiciones, los materiales dúctiles pueden exhibir un comportamiento quebradizo. Las condiciones de carga rápida, baja temperatura y tensión triaxial pueden causar que los materiales dúctiles fallen sin deformación previa.[3]
Fractura dúctil
[editar]
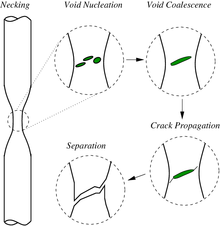
En la fractura dúctil, se produce una deformación plástica extensa (cuello) antes de la fractura. Los términos ruptura o ruptura dúctil describen la falla final de los materiales dúctiles cargados en tensión. La gran plasticidad hace que la grieta se propague lentamente debido a la absorción de una gran cantidad de energía antes de la fractura.[6][7]

Debido a que la ruptura dúctil implica un alto grado de deformación plástica, el comportamiento de fractura de una grieta en propagación, tal como se modeló anteriormente, cambia fundamentalmente. Parte de la energía de las concentraciones de tensión en las puntas de las grietas se disipa por la deformación plástica antes de la grieta a medida que se propaga.
Los pasos básicos en la fractura dúctil son la formación de huecos, la fusión de huecos (también conocida como formación de grietas), la propagación de grietas y las fallas, que a menudo resultan en una superficie de falla en forma de copa y cono. Los huecos generalmente se unen alrededor de precipitados, fases secundarias, inclusiones y en los límites de grano en el material. La fractura dúctil es típicamente transgranular y la deformación debida al deslizamiento por dislocación puede causar el labio cortante característico de la fractura de copa y cono.[8]
Modos de fractura y características
[editar]Hay tres convenciones estándar para definir desplazamientos relativos en materiales elásticos con el fin de analizar la propagación de grietas[3] según lo propuesto por Irwin.[9] Además, la fractura puede implicar una tensión uniforme o una combinación de estos modos.[4]

- Grieta modo I: Modo de apertura (una tensión de tensión normal al plano de la grieta)
- Grieta modo II: modo deslizante (un esfuerzo cortante que actúa paralelo al plano de la grieta y perpendicular al frente de la grieta)
- Grieta modo III: modo de rasgado (un esfuerzo cortante que actúa paralelo al plano de la grieta y paralelo al frente de la grieta)
La manera en que una grieta se propaga a través de un material da una idea del modo de fractura. Con la fractura dúctil, una grieta se mueve lentamente y se acompaña de una gran cantidad de deformación plástica alrededor de la punta de la grieta. Una grieta dúctil generalmente no se propagará a menos que se aplique un esfuerzo mayor y generalmente deje de propagarse cuando se elimine la carga.[4] En un material dúctil, una grieta puede progresar a una sección del material donde las tensiones son ligeramente más bajas y detenerse debido al efecto embotado de las deformaciones plásticas en la punta de la grieta. Por otro lado, con fractura frágil, las grietas se extienden muy rápidamente con poca o ninguna deformación plástica. Las grietas que se propagan en un material quebradizo continuarán creciendo una vez iniciadas.
La propagación de grietas también se clasifica por las características de grietas a nivel microscópico. Una grieta que pasa a través de los granos dentro del material está sufriendo una fractura transgranular. Una grieta que se propaga a lo largo de los límites del grano se denomina fractura intergranular. Típicamente, los enlaces entre los granos de material son más fuertes a temperatura ambiente que el material en sí mismo, por lo que es más probable que ocurra una fractura transgranular. Cuando las temperaturas aumentan lo suficiente como para debilitar los enlaces de grano, la fractura intergranular es el modo de fractura más común.[4]
Prueba de fractura
[editar]La fractura en los materiales se estudia y cuantifica de múltiples maneras. La fractura está determinada en gran medida por la resistencia a la fractura (), por lo que a menudo se realizan pruebas de fractura para determinar esto. Las dos técnicas más utilizadas para determinar la resistencia a la fractura son la prueba de flexión de tres puntos y la prueba de tensión compacta.
Al realizar la tensión compacta y las pruebas de flexión de tres puntos, se puede determinar la resistencia a la fractura a través de la siguiente ecuación:
Donde:
- es una ecuación derivada empíricamente para capturar la geometría de la muestra de prueba
- es el estrés por fractura y
- es la longitud de la grieta
Para alcanzar con precisión , el valor de debe medirse con precisión. Esto se hace tomando la pieza de prueba con su muesca de longitud fabricada y afilar esta muesca para emular mejor una punta de grieta que se encuentra en materiales del mundo real.[10] El pretensado cíclico de la muestra puede inducir una grieta por fatiga que extiende la grieta desde la longitud de muesca fabricada de a . Este valor se usa en las ecuaciones anteriores para determinar .[11]
Después de esta prueba, la muestra se puede reorientar de manera que una mayor carga de una carga (F) extenderá esta grieta y, por lo tanto, se puede obtener una curva de deflexión de carga versus muestra. Con esta curva, se puede obtener la pendiente de la porción lineal, que es la inversa de la conformidad del material. Esto se usa para derivar f (c/a) como se definió anteriormente en la ecuación. Con el conocimiento de todas estas variables, entonces se puede calcular.
Fractura frágil de cerámica y vidrios inorgánicos
[editar]La cerámica y los vidrios inorgánicos tienen un comportamiento de fractura que difiere del de los materiales metálicos. Las cerámicas tienen altas resistencias y funcionan bien a altas temperaturas debido a que la resistencia del material es independiente de la temperatura. Las cerámicas tienen baja tenacidad según lo determinado por pruebas bajo una carga de tracción; a menudo, la cerámica tiene valores que son ~ 5% de los encontrados en metales.[11] Sin embargo, la cerámica generalmente se carga en compresión en el uso diario, por lo que la resistencia a la compresión a menudo se conoce como la resistencia; esta resistencia a menudo puede exceder la de la mayoría de los metales. Sin embargo, la cerámica es frágil y, por lo tanto, la mayoría del trabajo realizado gira en torno a la prevención de fracturas frágiles. Debido a cómo se fabrican y procesan las cerámicas, a menudo hay defectos preexistentes en el material que introducen un alto grado de variabilidad en la fractura frágil del Modo I. Por lo tanto, hay una naturaleza probabilística a tener en cuenta en el diseño de la cerámica. La distribución de Weibull predice la probabilidad de supervivencia de una fracción de muestras con un cierto volumen que sobrevive a una tensión sigma de tensión, y a menudo se usa para evaluar mejor el éxito de una cerámica para evitar fracturas.
Fracasos notables de fractura
[editar]Las fallas causadas por fracturas frágiles no se han limitado a ninguna categoría particular de estructura de ingeniería.[3] Aunque la fractura frágil es menos común que otros tipos de fallas, los impactos en la vida y la propiedad pueden ser más graves. Los siguientes fracasos históricos notables se atribuyeron a fracturas frágiles:
- Recipientes a presión: gran inundación de melaza en 1919,[3] falla del tanque de melaza de Nueva Jersey en 1973[4]
- Puentes: colapso del tramo del puente King Street en 1962, colapso del puente de plata en 1967, falla parcial del puente Hoan en 2000
- Barcos: Titanic en 1912, Barcos de la libertad durante la Segunda Guerra Mundial, SS Schenectady en 1943
Véase también
[editar]Notas
[editar]- ↑ Una situación simple de tracción controlada por la carga sería soportar una muestra desde arriba y colgar un peso del extremo inferior. La carga sobre el espécimen es entonces independiente de su deformación.
- ↑ Una situación simple de tracción controlada por desplazamiento sería unir una jack muy rígida a los extremos de una muestra. A medida que el gato se extiende, controla el desplazamiento de la muestra; la carga sobre la muestra depende de la deformación.
Referencias
[editar]- ↑ Cherepanov, G.P., Mechanics of Brittle Fracture.
- ↑ a b Degarmo, E. Paul; Black, J T.; Kohser, Ronald A. (2003), Materials and Processes in Manufacturing (9th edición), Wiley, p. 32, ISBN 0-471-65653-4..
- ↑ a b c d e f Rolfe, John M. Barsom, Stanley T. (1999). Fracture and fatigue control in structures : applications of fracture mechanics (3. edición). West Conshohocken, Pa.: ASTM. ISBN 0803120826.
- ↑ a b c d e f Campbell, edited by F.C. (2012). Fatigue and fracture : understanding the basics. Materials Park, Ohio: ASM International. ISBN 978-1615039760.
- ↑ C. H. Chen; H. P. Zhang; J. Niemczura; K. Ravi-Chandar; M. Marder (November 2011). «Scaling of crack propagation in rubber sheets». Europhysics Letters 96 (3): 36009. Bibcode:2011EL.....9636009C. doi:10.1209/0295-5075/96/36009.
- ↑ Perez, Nestor (2016). Fracture Mechanics (2nd edición). Springer. ISBN 978-3319249971.
- ↑ Callister, William D., Jr. (2018). Materials science and engineering : an introduction (8th edición). pp. 236-237. ISBN 978-1-119-40539-9. OCLC 992798630.
- ↑ Askeland, Donald R. (January 2015). The science and engineering of materials. Wright, Wendelin J. (Seventh edición). Boston, MA. pp. 236-237. ISBN 978-1-305-07676-1. OCLC 903959750.
- ↑ Jin, C.T. Sun, Z.-H. (2012). Fracture mechanics. Waltham, MA: Academic Press. ISBN 9780123850010.
- ↑ EFM - Stress concentration at notches a closer look
- ↑ a b Courtney, Thomas H. (2000), Mechanical behavior of materials (3nd edición), McGraw Hill, ISBN 1-57766-425-6..
Otras lecturas
[editar]- Alireza Bagher Shemirani, Haeri, H., Sarfarazi, V., Hedayat, A., Un artículo de revisión sobre investigaciones experimentales sobre el comportamiento de falla de la articulación no persistente. Geomecánica e Ingeniería, vol. 13, núm. 4, (2017), 535–570, [1]
- Dieter, GE (1988) Metalurgia Mecánica ISBN 0-07-100406-8
- A. Garcimartin, A. Guarino, L. Bellon y S. Cilberto (1997) "Propiedades estadísticas de los precursores de fracturas". Physical Review Letters, 79, 3202 (1997)
- Callister, Jr., William D. (2002) Ciencia e ingeniería de materiales: una introducción. ISBN 0-471-13576-3
- Peter Rhys Lewis, Colin Gagg, Ken Reynolds, CRC Press (2004), Ingeniería de materiales forenses: estudios de casos.
Enlaces externos
[editar]- Museo virtual de productos fallidos en http://materials.open.ac.uk/mem/index.html
- Fractura y reconstrucción de un tazón de arcilla
- Fractura dúctil
















