Diferencia entre revisiones de «Fórmula bien formada»
mSin resumen de edición |
Deshecha la edición 30701676 de Luis Felipe Schenone (disc.) |
||
| Línea 1: | Línea 1: | ||
[[Archivo:Entidades sintácticas 2.svg|thumb|230px|right|Esta imagen muestra la relación entre las [[Cadena de caracteres|cadenas de caracteres]], las |
[[Archivo:Entidades sintácticas 2.svg|thumb|230px|right|Esta imagen muestra la relación entre las [[Cadena de caracteres|cadenas de caracteres]], las fórmulas bien formadas y los [[teorema]]s. En algunos sistemas formales, sin embargo, el conjunto de los teoremas coincide con el de las fórmulas bien formadas.]] |
||
En [[lógica matemática]], una '''fórmula bien formada''', también llamada '''palabra''', '''expresión''' o '''fórmula''', y a menudo abreviada '''fbf''', es una [[cadena de caracteres]] generada según una [[gramática formal]] a partir de un [[vocabulario (lógica)|alfabeto]] dado. Un lenguaje formal se define como el conjunto de todas sus fórmulas bien formadas. |
En [[lógica matemática]], una '''fórmula bien formada''', también llamada '''palabra''', '''expresión''' o '''fórmula''', y a menudo abreviada '''fbf''', es una [[cadena de caracteres]] generada según una [[gramática formal]] a partir de un [[vocabulario (lógica)|alfabeto]] dado. Un lenguaje formal se define como el conjunto de todas sus fórmulas bien formadas. |
||
Revisión del 18:44 18 oct 2009
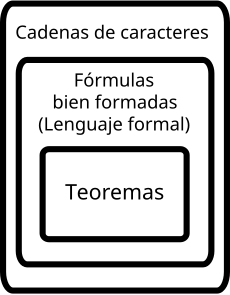
En lógica matemática, una fórmula bien formada, también llamada palabra, expresión o fórmula, y a menudo abreviada fbf, es una cadena de caracteres generada según una gramática formal a partir de un alfabeto dado. Un lenguaje formal se define como el conjunto de todas sus fórmulas bien formadas.
Por ejemplo, un alfabeto podría ser el conjunto {a,b}, y una gramática podría definir a las fórmulas bien formadas como aquellas cadenas que tienen el mismo número de caracteres a que b. Entonces, algunas fórmulas bien formadas del lenguaje serían: ab, ba, abab, ababba, etc. El lenguaje formal sería el conjunto de todas esas fórmulas bien formadas.
En la lógica formal, las demostraciones son secuencias de fórmulas bien formadas con ciertas propiedades, donde la última fórmula de la secuencia es aquello que se demuestra. Esta fórmula final se llama teorema cuando juega un papel importante en la teoría siendo desarrollada, o lema cuando juega un papel accesorio en la demostración de una teorema.
Véase también
Enlaces externos
- Fórmulas bien formadas en Lógica de predicados de primer orden (en inglés)
- Fórmulas bien formadas en ProvenMath (en inglés)
