Dendrograma
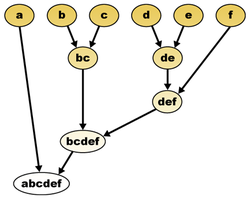
Un dendrograma o diagrama de árbol es un tipo de representación gráfica o diagrama de datos en forma de árbol (gr. δένδρον déndron 'árbol'). Organiza los datos en subcategorías que se van dividiendo en otros hasta llegar al nivel de detalle deseado (asemejándose a las ramas de un árbol que se van dividiendo en otras sucesivamente).[1]
Este tipo de representación permite apreciar claramente las relaciones de agrupación entre los datos e incluso entre grupos de ellos, aunque no las relaciones de similitud o cercanía entre categorías.[1]
En los algoritmos de agrupamiento
[editar]En los algoritmos de agrupamiento, el dendrograma ilustra las agrupaciones jerárquicas más derivadas de dichos algoritmos.[2] Los dendrogramas, en este aspecto, aportan una representación mejor de las agrupaciones de datos, respecto a otras representaciones.[3]
Referencias
[editar]- ↑ a b Creadores de dendrograma en línea Consultado el 29 de mayo de 2023.
- ↑ Cómo funciona Dendrograma Consultado el 29 de mayo de 2023.
- ↑ Tutorial del Algoritmo de Agrupamiento Jerárquico en Python Consultado el 29 de mayo de 2023.
