Método de orbitales moleculares como una combinación lineal de orbitales atómicos
Una Combinación Lineal de Orbitales Atómicos o CLOA es una superposición cuántica de orbitales atómicos y una técnica para calcular orbitales moleculares en química cuántica.[1] En mecánica cuántica, las configuraciones electrónicas de átomos son descritas como funciones de ondas. En matemáticas, estas funciones de onda son un conjunto base de funciones, las funciones bases, las cuales describen los electrones de un átomo dado. En reacciones químicas, las funciones de ondas orbitales son modificadas, esto es, la forma de la nube de electrones es cambiada de acuerdo al tipo de átomos participantes en el enlace químico.
Se introdujo en 1929 por John Lennard-Jones, con la descripción de la vinculación en las moléculas diatómicas de la principal de la primera fila de la tabla periódica, pero había sido usada antes por Pauling para el H2+.[2][3]
Una descripción matemática es:
o
donde es un orbital molecular representado como la suma de orbitales atómicos , cada uno multiplicado por su correspondiente coeficiente . Son coeficientes son los pesos de las contribuciones de los orbitales atómicos para el orbital molecular.
Los orbitales son expresados como una combinación lineal de funciones bases, y las funciones base son funciones de un electrón centrados en el núcleo de los componentes atómicos de la molécula. Los orbitales atómicos utilizados son generalmente aquellos átomos de hidrógeno, ya que estos son conocidos analíticamente, como los orbitales tipo Slater, pero existe la posibilidad de elegir otros como las funciones Gaussianas de los conjuntos base estándar.
Minimizando la energía total del sistema, un apropiado conjunto de coeficientes de la combinación lineal es determinado. Esta aproximación cuantitativa es hoy en día conocida como el método de Hartree-Fock. Sin embargo, desde el desarrollo de la química computacional, el método CLOA a menudo no se refiere a una verdadera optimización de la función de onda, sino que a un debate cualitativo el cual es muy útil para predecir y racionalizar resultados obtenidos mediante métodos más modernos. En este caso, la forma de los orbitales atómicos y sus respectivas energías son deducidas aproximadamente de la compactación de energía de los orbitales atómicos de los átomos individuales (o fragmentos moleculares) y aplicando algunas recetas conocidas el nivel de repulsión y cosas por el estilo. Los gráficos mostrados para hacer más clara esta discusión son llamados diagramas de correlación. Las requeridas energías de los orbitales atómicos pueden venir de los cálculos o directamente de experimentos mediante el teorema de Koopmans.
Esto es hecho utilizando la simetría de las moléculas y los orbitales involucrados en los enlaces. el primer paso en este proceso es asignar un grupo puntual a la molécula. Un claro ejemplo es el agua, la cual es de simetría C2v. Entonces, una representación reducible está determinada por la siguiente demostración del agua:
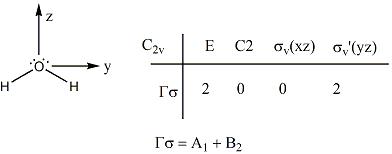
Cada operación en el grupo puntual se realiza también a la molécula. El número de enlaces que no son tocados es el carácter de esta operación. La representación reducible es descompuesta en la suma de representaciones irreductibles. Estas representaciones irreductibles corresponden a la simetría de los orbitales involucrados.
El diagrama de orbital molecular provee un simple y cualitativa tratamiento CLOA:

Teorías cuantitativas son el método Hückel, el método Hückel extendido y el método Pariser–Parr–Pople.
Véase también
[editar]Enlaces externos
[editar]- Approximate LCAO molecular orbital theroy (en inglés).
Referencias
[editar]- ↑ Huheey, James. Inorganic Chemistry: Principles of Structure and Reactivity.
- ↑ Werner Kutzelnigg. Friedrich Hund and Chemistry, con ocasión del centenario del nacimiento de Hund. Angewandte Chemie, 35, 573 - 586, (1996).
- ↑ Robert S. Mulliken's Nobel Lecture. Science, 157, no. 3785, 13 - 24, (1967).






