Árbol (informática)

En ciencias de la computación y en informática, un árbol es un tipo abstracto de datos (TAD) ampliamente usado que imita la estructura jerárquica de un árbol, con un valor en la raíz y subárboles con un nodo padre, representado como un conjunto de nodos enlazados.
Una estructura de datos de árbol se puede definir de forma recursiva (localmente) como una colección de nodos (a partir de un nodo raíz), donde cada nodo es una estructura de datos con un valor, junto con una lista de referencias a los nodos (los hijos), con la condición de que ninguna referencia esté duplicada ni que ningún nodo apunte a la raíz.
Alternativamente, un árbol se puede definir de manera abstracta en su conjunto como un árbol ordenado, con un valor asignado a cada nodo. Ambas perspectivas son útiles: mientras que un árbol puede ser analizado matemáticamente, realmente es representado como una estructura de datos en la que se trabaja con cada nodo por separado (en lugar de como una lista de nodos y una lista de adyacencia entre nodos, como un grafo). Mirando a un árbol como conjunto, se puede hablar de el nodo padre de un nodo dado, pero en general se habla de una estructura de datos de un nodo dado que sólo contiene la lista de sus hijos sin referencia a su padre (si lo hay).
Definición[editar]
 |
 |
 |
 |
 |
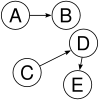
Un árbol es una estructura (posiblemente no lineal) de datos compuesta de nodos, vértices y aristas que es acíclica. Un árbol que no tiene ningún nodo se llama árbol vacío o nulo. Un árbol que no está vacío consta de un nodo raíz y potencialmente muchos niveles de nodos adicionales que forman una jerarquía.
Terminología utilizada en árboles[editar]
- Raíz: El nodo superior de un árbol.
- Hijo: Un nodo conectado directamente con otro cuando se aleja de la raíz.
- Padre: La noción inversa de hijo.
- Hermanos: Un conjunto de nodos con el mismo padre.
- Descendiente: Un nodo accesible por descenso repetido de padre a hijo.
- Ancestro: Un nodo accesible por ascenso repetido de hijo a padre.
- Hoja: Un nodo sin hijos.
- Nodo interno: Un nodo con al menos un hijo.
- Grado: Número de subárboles de un nodo.
- Brazo: La conexión entre un nodo y otro.
- Camino: Una secuencia de nodos y brazos conectados con un nodo descendiente.
- Nivel: El nivel de un nodo se define por 1 + (el número de brazos entre el nodo y la raíz).
- Altura de un nodo: La altura de un nodo es el número de brazos en el camino más largo entre ese nodo y una hoja.
- Altura de un árbol: La altura de un árbol es la altura de su nodo raíz.
- Profundidad: La profundidad de un nodo es el número de brazos desde la raíz del árbol hasta un nodo.
- Bosque: Un bosque es un conjunto de árboles n ≥ 0 disjuntos.
- Rama: Una ruta del nodo raíz a cualquier otro nodo.
Tipo de datos frente a la estructura de datos[editar]
Hay una distinción entre un árbol como un tipo de datos abstracto y como una estructura concreta de datos, de forma análoga a la distinción entre una lista y lista enlazada. Como tipo de dato, un árbol tiene un valor e hijos, y los hijos son a su vez subárboles; el valor y los hijos de un árbol se interpreta como el valor del nodo raíz y los subárboles de los hijos del nodo raíz. Para permitir que los árboles puedan ser finitos, hay que, o bien permitir que la lista de los hijos pueda estar vacía, o permitir que los árboles puedan estar vacíos, en cuyo caso la lista de los hijos pueden ser de tamaño fijo (factor de ramificación, especialmente 2 o binario), si se desea.
Como una estructura de datos, un árbol vinculado es un grupo de nodos, donde cada nodo tiene un valor y una lista de referencias a otros nodos (sus hijos). Esta estructura de datos realmente define a un grafo dirigido,[1] porque puede tener bucles o varias referencias al mismo nodo, del mismo modo que una lista enlazada. Luego también existe el requisito de que no hay dos referencias que apuntan al mismo nodo (que cada nodo tiene como máximo un solo padre, y de hecho todos lo tienen, a excepción de la raíz), y un árbol que viola esto es árbol corrupto.
Debido al uso de referencias a los árboles en la estructura de datos de un árbol enlazado, a menudo se habla de árboles en los que implícitamente están siendo representados por referencias al nodo raíz, ya que esto es, normalmente, la forma en la que se aplican realmente. Por ejemplo, en lugar de un árbol vacío, uno puede tener una referencia nula: un árbol nunca está vacío, sino que una referencia a un árbol puede ser nula.
Recursividad[editar]
De forma recursiva, un árbol como un tipo de datos se define como un valor (de un cierto tipo de datos, posiblemente vacía), junto con una lista de los árboles (posiblemente una lista vacía), los subárboles de sus hijos:
t: v [t[1], ..., t[k]]
(Un árbol t se compone de un valor v y una lista de otros árboles.)
Más elegantemente, a través de la recursión mutua, de los cuales un árbol es uno de los ejemplos más básicos, un árbol se puede definir en términos de un bosque (una lista de árboles), donde un árbol consta de un valor y un bosque (los subárboles de sus hijos):
f: [t[1], ..., t[k]] t: v f
Tenga en cuenta que esta definición es en términos de valores, y es apropiada en lenguaje funcional (se asume la transparencia referencial); diferentes árboles no tienen conexión, ya que son simplemente listas de valores.
Como una estructura de datos, un árbol se define como un nodo (la raíz), que a su vez consta de un valor (de algún tipo de datos, posiblemente vacío), junto con una lista de referencias a otros nodos (lista posiblemente vacía y referencias posiblemente nulas):
n: v [&n[1], ..., &n[k]]
(Un nodo n se compone de un valor v y una lista de referencias a otros nodos.)
Esta estructura de datos define un grafo dirigido,[1] y para que sea un árbol hay que añadir una condición en su estructura global (en su topología), y esto es que a lo sumo una referencia puede apuntar a cualquier nodo dado (un nodo tiene como máximo un solo padre), y ningún nodo del árbol puede apuntar a la raíz. De hecho, todos los nodos (que no sean la raíz) deben tener exactamente un padre, y la raíz no debe tener ningún padre.
De hecho, dada una lista de nodos, y para cada nodo de una lista de referencias a sus hijos, no se puede saber si esta estructura es un árbol o no sin analizar su estructura global, como se define a continuación.
Teoría de tipos[editar]
Como un tipo abstracto de datos (TAD), el tipo de árbol abstracto T con los valores de algún tipo E se define utilizando el tipo abstracto de los bosques F (lista de árboles), por las funciones:
- valor: T → E
- hijo: T → F
- nulo: () → F
- nodo: E × F → T
con los axiomas:
- valor(nodo(e, f)) = e
- hijo(nodo(e, f)) = f
En términos de la teoría de tipos, un árbol es un tipo inductivo definido por los constructores nulo (bosque vacío) y nodo (árbol con raíz con valor dado e hijos).
Matemáticamente[editar]
Visto en su conjunto, una estructura de datos en árbol es un árbol ordenado, generalmente con valores unidos a cada nodo. Concretamente, es (si se requiere que no sea vacío):
- Un árbol arraigado en dirección contraria a la raíz (un término más estrecho es una arborescencia), significa:
- Un grafo dirigido.
- Cuyo grafo no dirigido subyacente es un árbol (dos vértices están conectados por exactamente un camino simple).
- Con una raíz destacada (un vértice se designa como la raíz).
- Lo que determina la dirección en los brazos (flechas que apuntan fuera de la raíz; dado un brazo, el nodo desde donde la flecha apunta se llama el padre y el nodo al que apunta se llama el hijo).
Junto con:
- Una ordenación en los nodos hijos de un nodo dado, y un valor (de algún tipo de datos) en cada nodo.
A menudo, los árboles tienen un factor de ramificación de dos nodos hijo (posiblemente vacíos, por lo tanto, como máximo dos nodos secundarios no vacíos). En estos casos se habla de un árbol binario.
Permitir árboles vacíos hace algunas definiciones simples un poco más complicadas: un árbol con raíz no debe estar vacío, por lo tanto, si a los árboles vacíos se le asigna la definición anterior, en su lugar se convierte en un árbol vacío, o un árbol arraigado de tal manera que .... Por otro lado, los árboles vacíos se simplifican definiendo un factor de ramificación fijo: con árboles vacíos, un árbol binario es un árbol de tal manera que cada nodo tiene exactamente dos hijos, cada uno de los cuales es un árbol (posiblemente vacío). Los conjuntos de operaciones en un árbol deben incluir la operación de tenedor.
Terminología[editar]
Un nodo es una estructura que puede contener un valor o condición, o representar una estructura de datos separada (que puede llegar a ser un árbol). Cada nodo en un árbol tiene cero o más nodos hijo, que se disponen debajo de este en el árbol (por convenio, los árboles se dibujan de arriba abajo). Un nodo que tiene un hijo se llama el nodo padre del hijo (o nodo superior). Todos los nodos tienen al menos un padre.
Un nodo interno (también conocido como un nodo inferior o nodo rama) es cualquier nodo de un árbol que tiene nodos secundarios. De manera similar, un nodo externo (también conocido como un nodo exterior, nodo hoja, o nodo terminal) es cualquier nodo que no tiene nodos hijos.
El nodo más alto en un árbol se llama el nodo raíz. Dependiendo de la definición, un árbol puede ser obligado a tener un nodo raíz (en cuyo caso ningún árbol estaría vacío), o que se les permita estar vacíos, en cuyo caso no necesariamente tienen un nodo raíz. Siendo el nodo superior, el nodo raíz no tendrá un padre. Es el nodo en el que los algoritmos comienzan, ya que, como estructura de datos que es, sólo se puede pasar de padres a hijos. Tenga en cuenta que algunos algoritmos comienzan en la raíz, pero primero visitan a los nodos hoja (acceden al valor de los nodos hoja), y acceden por último a la raíz (es decir, que acceden por primera vez a los hijos de la raíz, pero solo acceder al valor de la raíz como último paso). Todos los demás nodos pueden ser accedidos siguiendo los brazos o enlaces. (En la definición formal, cada uno de esos caminos es único.) En los diagramas, el nodo raíz se extrae convencionalmente en la parte superior. En algunos árboles, tales como los montículos, el nodo raíz tiene propiedades especiales. Cada nodo en un árbol puede ser visto como el nodo raíz del subárbol con raíz en ese nodo.

La altura de un nodo es la longitud de la trayectoria descendente más larga a una hoja desde ese nodo. La altura de la raíz es la altura del árbol. La profundidad de un nodo es la longitud de la trayectoria a su raíz (es decir, su camino hacia la raíz). Esto es necesario comúnmente en la manipulación de diversos árboles auto balanceables (árboles AVL, en particular). El nodo raíz tiene una profundidad cero, los nodos hoja tienen altura cero, y un árbol con un solo nodo (por lo tanto, tanto una raíz y una hoja) tienen profundidad y altura cero. Convencionalmente, un árbol vacío (árbol con ningún nodo, si es que están permitidos) tienen profundidad y altura -1.
Un subárbol de un árbol T es un árbol que consiste en un nodo en T y todos sus descendientes en T.[2] Luego los nodos se corresponden con los subárboles (a cada nodo le corresponde el subárbol de sí mismo y todos sus descendientes) - el subárbol correspondiente al nodo raíz es todo el árbol, y cada nodo es el nodo raíz del subárbol que lo determina; el subárbol correspondiente a cualquier otro nodo se denomina el subárbol apropiado (por analogía a conjunto apropiado).
Dibujando árboles[editar]
Los árboles se dibujan a menudo en el plano. Los árboles ordenados pueden ser representados esencial y únicamente en el plano, y están por lo tanto llamados árboles de plano, de la siguiente manera: si uno fija un orden convencional (por ejemplo, en el sentido de las agujas del reloj), y dispone a los nodos secundarios en ese orden (primer brazo entrante de un padre, a continuación, primer brazo de hijo, etc.), esto produce una incrustación del árbol en el plano. A la inversa, tal incrustación determina un orden de los nodos secundarios.
Si uno coloca la raíz en la parte superior (padres por encima de los niños, como en un árbol genealógico) y coloca todos los nodos que están a una distancia dada desde la raíz (en términos de número de aristas: el nivel de un árbol) en una línea horizontal dada, se obtiene un dibujo estándar del árbol. Dado un árbol binario, el primer hijo es el de la izquierda (el nodo de la izquierda), y el segundo hijo está a la derecha (el nodo de la derecha).
Representaciones[editar]
Hay muchas maneras diferentes para representar árboles; las representaciones más comunes representan a los nodos dinámicamente como registros con punteros a sus hijos, a sus padres, o a ambos, o como elementos de un vector, con relaciones entre ellos determinadas por sus posiciones en este (por ejemplo, un montículo binario).
De hecho, un árbol binario puede ser implementado como una lista de listas (una lista donde los valores son listas): la cabeza de una lista (el valor del primer término) es el hijo izquierdo, mientras que la cola (la lista de los términos segundo y siguientes) es el hijo derecho. Esto puede ser modificado para permitir que los valores, como en las listas de expresión simbólica (expresión S), en donde la cabeza (valor de primer término) es el valor del nodo, la cabeza de la cola (valor de segundo término) sea el hijo izquierdo, y la cola de la cola (lista de términos sucesorios) sea el hijo derecho.
En general un nodo en un árbol no tendrá punteros a sus padres, pero esta información puede ser incluida (ampliando la estructura de datos para incluir también un puntero al vector) o almacenarse por separado. Alternativamente, los enlaces ascendentes pueden ser incluidos en los datos del nodo hijo, como en un árbol binario enlazado.
Generalizaciones[editar]
Grafos[editar]
Si se piensa en los brazos (a nodos secundarios) como referencias, entonces un árbol es un caso especial de un grafo, y la estructura de datos de árbol se puede generalizar para representar un grafo dirigido mediante la eliminación de las restricciones de que un nodo puede solo tener a lo sumo un padre, y que no se permiten ciclos. Los brazos se consideran todavía como pares de nodos, sin embargo, los términos padres e hijos generalmente se sustituyen por terminología diferente (por ejemplo, fuente y objetivo). Existen diferentes estrategias de implementación: un grafo puede ser representado por la misma estructura de datos locales que un árbol (nodos con valor y listas de sus hijos), en el supuesto de que "la lista de los hijos" sea una lista de referencias, o globalmente por estructuras tales como listas de adyacencia.
En la teoría de grafos, un árbol es un grafo acíclico conectado; salvo indicación de lo contrario, en la teoría de grafos, los árboles y los grafos se supone que no están dirigidos. No hay correspondencia uno-a-uno entre dichos árboles y árboles como estructura de datos. Podemos tomar un árbol arbitrario sin dirección, y arbitrariamente escoger uno de sus vértices como la raíz, y hacer que todas sus brazos apunten en dirección contraria a la raíz - produciendo una arborescencia - y asignar un orden a todos los nodos. El resultado se corresponde a una estructura de datos de árbol. Escoger una raíz diferente o un orden diferente produce un grafo diferente.
Dado un nodo en un árbol, sus hijos definen un bosque ordenado (la unión de subárboles dados por todos sus hijos, o lo que es equivalente, tomar el subárbol dado por el propio nodo y borrar la raíz). Así como los subárboles son asiduos a la recursividad (como en una búsqueda por profundidad), los bosques son asiduos a la correcursión (como en una búsqueda por anchura).
A través de la recursión mutua, un bosque puede definirse como una lista de árboles (representados por nodos raíz), donde un nodo (de un árbol) se compone de un valor y un bosque (sus hijos):
f: [n[1], ..., n[k]] n: v f
Métodos de recorrido[editar]
Pasar a través de los elementos de un árbol por medio de las conexiones entre padres e hijos se llama recorrer el árbol, y la acción es un camino por el árbol. A menudo, una operación puede ser realizada cuando un puntero llega a un nodo en particular. Un camino en el que cada nodo padre es atravesado antes que sus hijos se llama camino de orden previo; un camino en el que los hijos son atravesadas antes que sus respectivos padres se llaman un camino de orden posterior; un camino en el que el subárbol izquierdo de un nodo, el nodo en sí, y finalmente su subárbol derecho son atravesadas se llama un orden transversal. (Esta última situación, en referencia a exactamente dos subárboles, un subárbol izquierdo y un subárbol derecho, es específicamente un árbol binario.) Un camino de orden de nivel lleva a cabo una búsqueda por anchura efectiva sobre la totalidad del árbol; los nodos son atravesados nivel por nivel, en donde el nodo raíz es visitado en primer lugar, seguido por sus nodos hijos directo y sus hermanos, seguidos de sus nodos nietos y sus hermanos, etc., hasta que todos los nodos en el árbol han sido atravesado.
Operaciones comunes[editar]
- Enumerar todos los elementos
- Enumerar la sección de un árbol
- Buscar un elemento
- Añadir un nuevo elemento en una determinada posición del árbol
- Borrar un elemento
- Podar: Borrar una sección entera de un árbol
- Injertar: Añadir una sección entera a un árbol
- Buscar la raíz de algún nodo
- Representar cada nodo como una variable en el montículo con punteros.
- Representar el árbol con un vector
Usos comunes[editar]
- Representar un dato jerárquicamente
- Almacenar un dato de tal modo que su búsqueda sea eficiente (ver búsqueda en árboles binarios y recorrido de árboles)
- Representar listas ordenadas de datos
- Como un flujo de trabajo para la composición de imágenes digitales
- Algoritmos de encaminamiento
Véase también[editar]
- Recorrido de árboles
- Árbol (teoría de grafos)
- Herencia múltiple
- Gramática generativa
- Agrupamiento jerárquico
- Partición binaria del espacio
- Recursión
- Montículo
Otros árboles[editar]
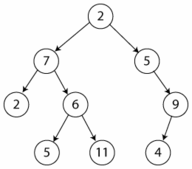
- Árboles Binarios
- Árbol de búsqueda binario auto-balanceable
- Árboles AVL
- Árboles Rojo-Negro
- Árbol AA
- Árbol de segmento
- Árboles Multicamino
- Árboles B (Árboles de búsqueda multicamino autobalanceados)
- Árbol-B+
- Árbol-B*
Referencias[editar]
- ↑ a b Adecuadamente, un gráfico dirigido ordenado y arraigado.
- ↑ Esto es diferente de la definición formal de subárbol utilizada en la teoría de grafos, donde es un subgrafo que forma un árbol - que no es necesario que incluya a todos sus descendientes. Por ejemplo, el nodo raíz, por sí mismo es un subárbol en la teoría de grafos, pero no en la teoría de estructura de datos (a menos que no haya descendientes)
Enlaces externos[editar]
- Esta obra contiene una traducción total derivada de «Tree (data structure)» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
