Función de producción de Cobb-Douglas
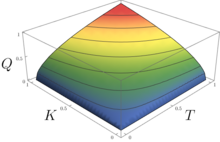
En economía y econometría, la función de producción de Cobb-Douglas es una forma de función de producción, ampliamente usada para representar las relaciones entre un producto y las variaciones de los insumos tecnología, trabajo y capital. Fue propuesta por Knut Wicksell (1851-1926) e investigada con respecto a la evidencia estadística concreta, por Charles Cobb y Paul Douglas en 1928.[1][2][3]
La función de producción Cobb-Douglas es un enfoque neoclásico para estimar la función de producción de un país y proyectar así su crecimiento económico esperado.
Capital, Trabajo y Tecnología[editar]
La función partió de la observación empírica de la distribución de la renta nacional total de Estados Unidos entre el capital y el trabajo. Los datos mostraron que se mantenía más o menos constante a lo largo del tiempo y a medida que crecía la producción, la renta del total de los trabajadores crecía en la misma proporción que la renta del conjunto de los empresarios. Douglas solicitó a Cobb establecer una función que resultara en participación constante de los dos factores si ganaban en su producto marginal.[4] Esta función de producción presenta la forma
- ,
donde:
- Y = producción total (el valor monetario de todos los bienes producidos durante un año)
- T = trabajo insumo
- K = capital insumo
- A = factor total de productividad
- α y β son las elasticidades producto del trabajo y el capital, respectivamente. Estos valores son constantes determinadas por la tecnología disponible.
La elasticidad del producto mide la respuesta del producto a un cambio en los niveles del trabajo o del capital usados en la producción, si permanecen constantes los demás factores. Por ejemplo, si α = 0,15, un aumento del 1% en la cantidad de trabajo, provocaría un incremento aproximado del 0,15% en el volumen del producto. Así, si:
- ,
La función de producción tiene rendimientos de escala constantes, es decir que si T y K aumenta cada uno el 20%, Q aumenta también el 20%. Esto significa que la función Cobb-Douglas es homogénea de grado 1 e implica que el costo mínimo es independiente del volumen de la producción y depende solo de los precios relativos de los factores de producción. Si
- ,
rendimientos de escala son descendentes, y si
los rendimientos de escala son crecientes.
Suponiendo competencia perfecta, α y β pueden ser obtenidos como la cuota de T y de K con respecto a Q. Un avance tecnológico que aumenta el parámetro A incrementa proporcionalmente el producto marginal de T y de K.
Evidencia estadística han mostrado que las proporciones de trabajo y capital con respecto al producto total fueron constantes a través del tiempo en los países desarrollados, lo cual explicaron Cobb y Douglas ajustando estadísticamente una regresión de mínimos cuadrados de su función de producción. En Estados Unidos el cociente entre la renta de trabajo y la renta total ha representado alrededor del 0,7 por un largo período y así lo corroboraron los datos obtenidos entre 1960 y 1996.[4] Esta distribución se explica mediante una función de producción Cobb-Douglas en la cual el parámetro α sea aproximadamente 0,7.[4]
Críticas[editar]
Actualmente algunos expertos, expresan dudas sobre la constancia de esta relación a través del tiempo.[5][6] Ni Cobb, ni Douglas aportaron una razón teórica por la cual los exponentes α y β deberían mantenerse constantes en el tiempo o entre sectores de la economía. Hay que recordar que la naturaleza de la maquinaria y de otros bienes de capital (K) difiere entre períodos y de acuerdo al bien que vaya a producirse. Así también las habilidades o calidades del trabajo (L).
Por otra parte, la función Cobb-Douglas no fue desarrollada en base de ningún conocimiento de la ingeniería, la tecnología, o de la gerencia del proceso de producción. Fue en cambio desarrollada por sus coincidencias con la teoría económica de sus atractivas características matemáticas, tales como la los rendimientos marginales decrecientes de los diferentes factores de producción.
No hay microfundamentos o análisis del comportamiento de los agentes individuales con respecto a esta función. Los economistas han insistido más recientemente en que hay que explicar la micrológica de procesos en gran escala, lo cual no logra la función Cobb-Douglas.
También existen críticas al uso de esta función desde la economía biofísica, las cuales ponen en duda su significado operacional.[7]
Origen[editar]
El origen de la función Cobb-Douglas se encuentra en la observación empírica de la distribución de la renta nacional total de Estados Unidos entre el capital y el trabajo. De acuerdo a lo que mostraban los datos, la distribución se mantenía relativamente constante a lo largo del tiempo. Concretamente el trabajo se llevaba un 70% y el capital un 30%. De esta forma, la función Cobb-Douglas representa una relación en donde las proporciones de trabajo y capital con respecto al producto total son constantes.
Simplificación de la función Cobb-Douglas[editar]
Para estimar el crecimiento económico futuro es más útil reformular la función Cobb-Douglas aplicando logaritmos naturales. Asumiendo que α + β = 1 (retornos constantes a escala) y unas pequeñas asunciones más podemos establecer la tasa de crecimiento económico en función de los cambios de los factores de producción:
%ΔY ≅ (%ΔA) + α(%ΔK) + (1-α)(%ΔL)
Donde:
%ΔY = Tasa de variación del PIB esperada
%ΔTFP = Crecimiento Productividad total de los factores (PTF)
%ΔK = Crecimiento Stock de capital
%ΔL = Crecimiento del número de empleados
α = Elasticidad del capital sobre la producción
Esta fórmula es muy utilizada en bolsa para estimar el crecimiento económico. Estudios empíricos sugieren que sería razonable asumir que el crecimiento del empleo (L) tiene un efecto lineal en el crecimiento del empleo.
Algunas aplicaciones[editar]
A pesar de las críticas, la función Cobb-Douglas ha sido aplicada en contextos diferentes a la producción. Ha sido aplicada a la función de utilidad, así:
donde x1 y x2 son las cantidades consumidas de un bien #1 y un bien #2.
La forma general de la función Cobb-Douglas:
- o , .
El índice corresponde a los factores de producción (por ejemplo las cantidades de trabajo o de capital utilizadas para producir un bien).
Por otra parte, el modelo de crecimiento de Solow[8] parte de una función Cobb-Douglas de producción
y concluye determinando la importancia crucial de la tecnología para el crecimiento continuado. En la investigación del ciclo económico, los modelos del ciclo real utilizan y profundizan los trabajos de Solow.[9]
Representaciones de la función[editar]
La función Cobb-Douglas puede ser estimada como una relación lineal usando la siguiente expresión: , donde:
- Q = Producto
- Ii = Insumos
- ai = Coeficientes del modelo
El modelo también puede representarse así:
También puede ser linearizada así:
donde son las cantidades consumidas de cada bien i y son las elasticidades de la demanda de servicios.
La Función de Producción Logarítmico Transcendental (translog) es una generalización de la función Cobb-Douglas. Los función de producción translog para tres factores es:
donde T = trabajo, K = capital, M = materiales y suministros, y Q = producto.
Derivada de una función CES[editar]
La función de elasticidad de sustitución constante (CES)
Cuando , la función CES se reducirá a una función Cobb-Douglas,
Prueba:
Aplicando la Regla de L'Hôpital:
Por consiguiente, .
Referencias[editar]
- ↑ Cobb, C.W. and P.H. Douglas (1928) "A Theory of Production", American Economic Review 18 (supplement): 139-165.
- ↑ Douglas, Paul H. (1934) The Theory of Wages. New York: The Macmillan Co.
- ↑ Cobb, C. W. y P. H. Douglas (1948) "Are there Laws of Production?"; The American Economic Review 38: 1-41.
- ↑ a b c Mankiw, N. George (2004) Macroeconomía: 93-96. Antoni Bosch editor. ISBN 84-95348-12-8
- ↑ Sylos-Labini, Paolo (1995) "Why the interpretation of the Cobb-Douglas production function must be radically changed"; Structural Change & Ec. Dyn. 6: 485-504.
- ↑ Fisher, F.M. (1992) Aggregation. Aggregate Production Functions and Related Topics. Cambridge, MA: The MIT Press.
- ↑ http://www.ipe.ro/rjef/rjef4_12/rjef4_2012p17-35.pdf
- ↑ Solow, R. M. (1957) "Technical Change and the Aggregate Production Function"; Review of Economics and Statistics 39:312-320.
- ↑ Prescott, E. (1986) "Theory ahead of business cycle measurement"; Federal Reserve Bank of Minneapolis Quarterly Review fall: 9-22.
Enlaces externos[editar]
- Anatomy of Cobb-Douglas Type Production Functions in 3D
- La Función de Producción Cobb-Douglas y la Economía Española.



















![{\displaystyle Q=A[\alpha K^{\gamma }+(1-\alpha )T^{\gamma }]^{\frac {1}{\gamma }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a4794b3bfee2e7c28f191487b56089cf4be402)


![{\displaystyle \ln(Q)=\ln(A)+{\frac {\ln[\alpha K^{\gamma }+(1-\alpha )T^{\gamma }]}{\gamma }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48e14fba348330d9936e5db95e9d4dbb5baf1594)

