Flujo de Fanno
El flujo de Fanno (por Gino Girolamo Fanno) es un tipo de flujo compresible interno en conductos que se caracteriza por ser adiabático, sin cambio de masa y de área constante pero con los efectos derivados de la fricción. Esta se considera una fricción viscosa en la pared del conducto. Es por tanto un flujo no isoentrópico. Aunque su resolución general es compresible, se aplica también a flujo incompresible.
Para una corriente con un número de Mach superior a 1 en un conducto lo bastante largo, la fricción desacelera el flujo hasta causar el bloqueo sónico. Para otra corriente con M<1, la fricción acelera el flujo hasta llegar a la misma situación para un conducto lo bastante largo. Se puede demostrar que para dicha situación de bloqueo, la entropía alcanza un máximo.
Teoría[editar]
El flujo de Fanno parte de la ecuación diferencial que relaciona el cambio en el número de Mach con la longitud del conducto dM/dx:
donde γ es el coeficiente de dilatación adiabática, f es el factor de fricción de Fanning (siendo 4f el factor de fricción de Darcy) y Dh es el diámetro hidráulico.
Asumiendo que el coeficiente de fricción se mantiene constante a lo largo del conducto, la ecuación diferencial se puede resolver fácilmente.[1][2] Sin embargo, no es fácil calcular los factores de fricción de un flujo supersónico (especialmente cuando se hace hipersónico).
Con dicha resolución se puede calcular la longitud de conducto hasta que se produce el bloqueo sónico L*:
Entalpía y entropía[editar]
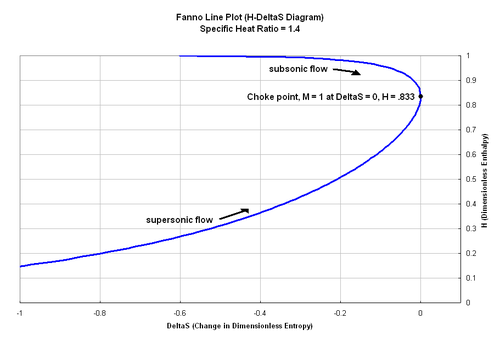
Igualmente importante para el modelo de Fanno es la evolución de la entropía (adimensionalizada en función del calor específico cp):.
Esta ecuación puede ser reescrita en función de un ratio entre la temperatura estática y la temperatura de remanso, lo que para gas perfecto es igual a la entalpía adimensional H. (). En efecto:
Dicha ecuación se puede usar para trazar un diagrama que relaciona la entalpía y la entropía, característico para el flujo de Fanno. El flujo alcanza su máxima entropía a H = 0.833 con el flujo bloqueado. De acuerdo a la segunda ley de la termodinámica, la entropía debe ser siempre creciendo, lo que demuestra que el flujo de Fanno tenderá siempre hacia M=1, tanto si es supersónico como si es subsónico.
Dicha curva define los estados posibles para un gas variando el momentum. El cambio en la cantidad de movimiento es causado por la fricción, que acelera o decelera el flujo (según sea subsónico o supersónico).[3]
Relaciones adicionales[editar]
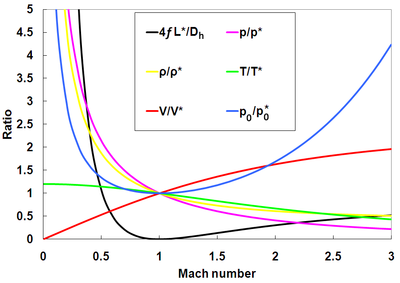
Como consecuencia de la definición del modelo, el área y gasto másico son constantes en el flujo. Además, al ser adiabático, la temperatura de remanso se mantiene constante.
Se pueden desarrollar ecuaciones para desarrollar la evolución de varias variables con respecto a los valores críticos (M=1). A continuación se muestran, usando el superíndice * para la garganta y dejando las variables sin ningún superíndice.
Se pueden obtener asimismo relaciones entre dos puntos arbitrarios relacionando ambas con la garganta.
Aplicaciones[editar]
El modelo de Fanno se suele usar en el estudio y diseño de toberas. La etapa convergente o divergente se suele modelar como flujo compresible con variaciones de sección mientras que las zonas de sección constante se calculan con el flujo de Fanno. Así, para unas condiciones aguas arriba en un punto 1 de las gráficas precedentes se puede calcular para averiguar el número de Mach a la salida y la posición de una onda de choque normal en el conducto. Con el índice dos se indica la garganta (donde M = 1 si se produce bloqueo). El punto 3 indica la salida de la tobera, donde el flujo cambia de isentrópico a Fanno. Con suficiente presión inicial, el flujo supersónico puede ser mantenido durante la región de área constante, similarmente al comportamiento de un túnel de viento supersónico.

El caso de estas gráficas muestra una situación en que dicha presión es insuficiente y se genera una onda de choque a través del conducto. Si una onda de choque está presente, el flujo pasa de supersónico a subsónico por medio de una onda de choque, para ser acelerado hasta recuperar M=1. En la siguiente figura el movimiento es siempre de izquierda a derecha para satisfacer la segunda ley de la termodinámica.


El flujo de Fanno también se suele usar con el Flujo de Rayleigh. Las curvas características de ambos modelos se cortan en dos puntos significativos ya que es donde puede pasarse de un flujo a otro. Esto se debe a que ambos modelos dan una entropía máxima para M=1, pero no coinciden en el valor de esta entropía. Si partimos de una entropía inicial si para Mi podemos definir los valores de esta entropía máxima según cada modelo según las siguientes ecuaciones:
Donde el resultado de igualar ambas ecuaciones nos da los puntos de intersección de ambas curvas características. El ejemplo se obtiene para valores de si = 0 y Mi = 3, lo que lleva igualando a:
Dicha solución ocurre tanto para ese número de Mach como para el valor de Mach tras una onda de choque. Para los valores del ejemplo eso son M = 3 y M=0.4752, como se puede comprobar en las tablas de valores para onda de choque normal.
Véase también[editar]
- Flujo compresible
- Flujo compresible con variaciones de sección
- Flujo de Rayleigh
- Gas perfecto
- Aerodinámica
- Bloqueo sónico
- Entalpía
- Entropía
Referencias[editar]
Enlaces externos[editar]
- Purdue University Adiabatic and Isothermal Fanno flow calculators
- University of Kentucky Fanno flow Webcalculator
- Maurice W. Downey, Gino Fanno


![{\displaystyle \ {\frac {4fL^{*}}{D_{h}}}=\left({\frac {1-M^{2}}{\gamma M^{2}}}\right)+\left({\frac {\gamma +1}{2\gamma }}\right)\ln \left[{\frac {M^{2}}{\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d3400a03fe159951756769bd5df8f2607a20b8)
![{\displaystyle \ \Delta S={\frac {\Delta s}{c_{p}}}=\ln \left[M^{\frac {\gamma -1}{\gamma }}\left(\left[{\frac {2}{\gamma +1}}\right]\left[1+{\frac {\gamma -1}{2}}M^{2}\right]\right)^{\frac {-(\gamma +1)}{2\gamma }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c679a2d173adae85d4f6436444b15048ec999f8b)

![{\displaystyle \ \Delta S={\frac {\Delta s}{c_{p}}}=\ln \left[\left({\frac {1}{H}}-1\right)^{\frac {\gamma -1}{2\gamma }}\left({\frac {2}{\gamma -1}}\right)^{\frac {\gamma -1}{2\gamma }}\left({\frac {\gamma +1}{2}}\right)^{\frac {\gamma +1}{2\gamma }}\left(H\right)^{\frac {\gamma +1}{2\gamma }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dab1f349013744ebcf2e6ceefa006a98f85ee8b)
![{\displaystyle {\begin{aligned}{\frac {p}{p^{*}}}&={\frac {1}{M}}{\frac {1}{\sqrt {\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}}\\{\frac {\rho }{\rho ^{*}}}&={\frac {1}{M}}{\sqrt {\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}\\{\frac {T}{T^{*}}}&={\frac {1}{\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}\\{\frac {V}{V^{*}}}&=M{\frac {1}{\sqrt {\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}}\\{\frac {p_{0}}{p_{0}^{*}}}&={\frac {1}{M}}\left[\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)\right]^{\frac {\gamma +1}{2\left(\gamma -1\right)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caf30572891bf439a34e222c067d4f14b8e76ab0)
![{\displaystyle {\begin{aligned}\Delta S_{F}&={\frac {s-s_{i}}{c_{p}}}=\ln \left[\left({\frac {M}{M_{i}}}\right)^{\frac {\gamma -1}{\gamma }}\left({\frac {1+{\frac {\gamma -1}{2}}M_{i}^{2}}{1+{\frac {\gamma -1}{2}}M^{2}}}\right)^{\frac {\gamma +1}{2\gamma }}\right]\\\Delta S_{R}&={\frac {s-s_{i}}{c_{p}}}=\ln \left[\left({\frac {M}{M_{i}}}\right)^{2}\left({\frac {1+\gamma M_{i}^{2}}{1+\gamma M^{2}}}\right)^{\frac {\gamma +1}{\gamma }}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31b696ced22bb1df158e11d46ce5b9f5a19b64b5)
![{\displaystyle \ \left(1+{\frac {\gamma -1}{2}}M_{i}^{2}\right)\left[{\frac {M_{i}^{2}}{\left(1+\gamma M_{i}^{2}\right)^{2}}}\right]=\left(1+{\frac {\gamma -1}{2}}M^{2}\right)\left[{\frac {M^{2}}{\left(1+\gamma M^{2}\right)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1031340758891c29e5707e01def7e1c5983b548d)