Cálculo de secciones de líneas eléctricas
El cálculo de secciones de líneas eléctricas es un método de cálculo para obtener la sección idónea de los conductores empleados, siendo el conjunto de conductores capaz de:
- transportar la potencia requerida con total seguridad;
- que dicho transporte se efectúe con un mínimo de pérdidas de energía;
- mantener los costes de instalación en unos valores aceptables.
A la hora de dimensionar un conductor se aplican tres criterios básicos:
- que su caída de tensión () esté dentro de los límites admisibles;
- que el calentamiento por efecto Joule no destruya el material aislante del conductor;
- que en caso de cortocircuito, no se destruya el conductor.
Cálculo por caída de tensión[editar]
La caída de tensión () se produce como consecuencia de la resistencia de los conductores. Como regla general, en España, se permite una () máxima de:[1]
- 3% para cualquier circuito interior de viviendas.
- 3 % en instalaciones de alumbrado.
- 5 % en el resto de instalaciones.
La normativa puede establecer otros valores para la caída de tensión máxima admisible. Existen diversas formas de calcular la sección mínima del conductor para diferentes situaciones:
- Líneas de corriente continua
donde S es la sección del conductor, la resistividad, la I la intensidad prevista en el conductor y la caída de tensión permitida.
- Líneas de corriente alterna monofásica
- Líneas de corriente alterna (trifásica)
donde:
- es caída de tensión en voltios.
- es el factor de potencia activa.
- es la longitud del cable en metros.
- es la resistividad en (Ω(mm2)/m
Momento eléctrico de una línea[editar]

El momento eléctrico de una línea es el producto de la carga eléctrica por la distancia hasta el origen. Puede considerarse como el equivalente de la línea constituido por un único tramo de línea con una única carga en su extremo.
- En corriente continua:
- En corriente alterna:
donde:
- M, momento eléctrico, en amperios por metro [A·m].
- L, longitud de la línea, en metros [m].
- I = intensidad de corriente eléctrica, en amperios [A].
- , factor de potencia, adimensional.
Líneas con cargas irregularmente repartidas[editar]
- Momento eléctrico:

- Expresión desarrollada para este caso:
- Es el método general de cálculo de líneas por caída de tensión.'
Líneas con cargas uniformemente repartidas[editar]
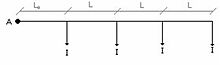
Son un caso particular de líneas con cargas irregularmente repartidas. Se pueden calcular como las anteriores, o mediante un método específico.
- Momento eléctrico:
- Expresión desarrollada para este caso:
Líneas alimentadas por ambos extremos a la misma tensión[editar]
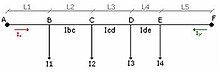
En este tipo de líneas aparece el punto de mínima tensión, que es aquel en donde la C.D.T. es máxima. Dicho punto puede considerarse como el centro de gravedad de la línea. Para su cálculo:
- Obtenemos el valor de e .
- Ahora, basándonos en la Ley de Nudos de Kirchhoff, vamos restando de izquierda a derecha las intensidades a , hasta el primer resultado negativo. Esta intensidad negativa debe coincidir, tanto si la calculamos de izquierda a derecha como de derecha a izquierda. El punto donde aparece dicha intensidad es el Punto de Mínima Tensión.
- Sustituimos el valor de la última intensidad empleada en los cálculos antes de llegar a un valor negativo por el valor obtenido.
División de la red por el punto de mínima tensión[editar]

Una vez seccionada la línea en dos ramas, calculamos cualquiera de las dos por uno de los métodos anteriores. El resultado será válido para las dos ramas.
Ejemplo de cálculo[editar]
Líneas en anillo[editar]

Estas líneas son, en realidad, líneas alimentadas por ambos extremos a la misma tensión, y se calculan de forma idéntica a las anteriores
Líneas con ramificaciones[editar]
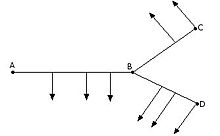
En este caso, se calcula la rama principal, según los métodos anteriores, considerando la suma de todas las cargas de las ramas secundarias aplicadas en el punto de unión entre las ramas principal y secundaria.
El principal inconveniente puede ser repartir la caída de tensión entre la rama principal y las extremas. Lo podemos hacer de forma heurística o calcular la caída de tensión óptima para conseguir un volumen mínimo de conductor (criterio económico).
Cálculo por calentamiento[editar]
En todo momento, el conductor ha de soportar la intensidad máxima del circuito sin deteriorarse. Por ello, la intensidad nominal del conductor ha de ser mayor a la intensidad máxima del circuito.
El elemento que va a limitar la temperatura máxima a la que es capaz de trabajar el cable es su aislamiento, generalmente de material plástico. Las temperaturas máximas admisibles para los distintos tipos de aislamiento son:[2]
| Material | Temperatura de servicio (°C) | Temperatura de cortocircuito (t< 5s)(°C) |
|---|---|---|
| PVC | 70 | 160 |
| Polietileno reticulado (XLPE) | 90 | 250 |
| Etileno-Propileno (EPR) | 90 | 250 |
Los nuevos aislamientos a base de poliolefinas termoplásticas (cables libres de halógenos) se consideran, a efectos de cálculo, como de PVC.
Cálculo por corriente máxima de cortocircuito[editar]
Por sus características (gran intensidad y corta duración), durante un cortocircuito se considera un calentamiento adiabático del conductor, es decir, todo el calor generado, se invierte en elevar la temperatura del cable.
Mediante la siguiente expresión[3] se puede calcular la corriente máxima de cortocircuito para una sección determinada:
donde:El cálculo de secciones de líneas eléctricas es un método de cálculo para obtener la sección idónea del conductor a emplear, siendo este capaz de:
- transportar la potencia requerida con total seguridad;
- que dicho transporte se efectúe con un mínimo de pérdidas de energía;
- mantener los costes de instalación en unos valores aceptables.
A la hora de dimensionar un conductor se aplican tres criterios básicos:
- que su caída de tensión () esté dentro de los límites admisibles;
- que el calentamiento por efecto Joule no destruya el material aislante del conductor;
- que en caso de cortocircuito, no se destruya el conductor.
Véase también[editar]
Referencias[editar]
- ↑ REBT 2002, ITC-19. Apartado 2.2.2: Secciones de los conductores. Caídas de tensión.
- ↑ Norma UNE 20460-5-523, Parte 523.1.3, tabla 52-A.
- ↑ Norma UNE 21145: Guía sobre la aplicación de los límites de temperatura de cortocircuito de los cables eléctricos de tensión nominal no superior a 0,6/1kV. (Norma derrogada)
Normas y reglamentos[editar]
- Norma UNE 20460-5-523: Intensidades admisibles en sistemas de conducción de cables.
- Para cables en cañerías embutidas o a la vista Pirelli Cables fabrica la línea Pirastic Ecoplus. Se trata de cables unipolares aislados en PVC según norma IRAM 2183, los coeficientes de corrección de la corriente admisible,son para dos cables se debe multiplicar por 1,10; si los cables instalados son de 4 a 6 multiplicar por 0,8 y si son de 7 a 9 cables el coeficiente de multiplicación será 0,7.
- Publicación Técnica Schneider PT-073 «Líneas y Cables». Schneider Electric. [1]
- Reglamento Electrotécnico de Baja Tensión, aprobado por el Real Decreto 842/2002 de 2 de agosto de 2002. [2]























