Puerta AND
| INPUT | OUTPUT | |
| A | B | A AND B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
La compuerta AND o puerta AND es una puerta lógica digital que implementa la conjunción lógica, se comporta de acuerdo a la tabla de verdad mostrada a la derecha; esta tendrá una salida ALTA (1), únicamente cuando los valores de ambas entradas sean ALTOS. Si alguna de estas entradas no son ALTAS, entonces tendrá un valor de salida BAJA (0). Desde el punto de vista funcional, la puerta AND es un multiplicador pues su salida es el producto de sus entradas.[1]
La expresión matemática de la compuerta AND es: Output = a*b
Variantes y numeraciones de AND[editar]
- Compuerta AND de 2 entradas = 74LS08
- Compuerta AND de 3 entradas = 74LS11
- Compuerta AND de 4 entradas = 74LS21
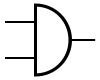
Símbolos[editar]
Hay tres símbolos para las puertas AND: el símbolo texano -Americano- (ANSI o "militar") y el símbolo IEC ("europeo" o "rectangular"), así como el símbolo DIN.[2] Para obtener más información, vea Puerta lógica.

|

|
|
| Símbolo ANSI o "Militar" | Símbolo IEC | Símbolo DIN |
La compuerta AND con entradas A, B y C; implementa de salida la siguiente expresión lógica
- .[1]
Implementaciones[editar]
 |
 |
 |
Las entradas digitales a y b causan que la salida F tenga el mismo resultado que la función AND. Normalmente, una puerta se diseña utilizando canal N (en la ilustración) o MOSFET's de canal P. si la salida se va a conectar a una carga en lugar de a otra puerta, es preferible usar la versión CMOS (N y P) para que no se reduzca el voltaje de salida cuando el resultado de la función sea verdadero.
Alternativas[editar]
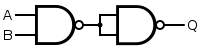
En caso de no estar disponibles puertas AND específicas, estas pueden ser implementadas usando puertas NAND o NOR. Las puertas NAND y NOR se consideran "puertas universales", lo que significa que utilizando exclusivamente cualquiera de ellas como base, se pueden implementar el resto de puertas AND, OR, NOT, XOR etc.[3]
| Puerta deseada | Construcción NAND | Construcción NOR |
|---|---|---|
 |
 |

|
Véase también[editar]
 Wikimedia Commons alberga una categoría multimedia sobre Puerta AND.
Wikimedia Commons alberga una categoría multimedia sobre Puerta AND.- Puerta OR
- Puerta NOT
- Puerta NAND
- Puerta NOR
- Puerta XOR
- Puerta XNOR
- Álgebra de Boole
- Puerta lógica
Referencias[editar]
- ↑ a b Acedo Sánchez, José (2013). Instrumentación y control básico de procesos. Ediciones Díaz de Santos. pp. 96, 98. ISBN 9788499695051.
- ↑ Carretero Montero, Alfonso (2009). Electrónica. Editex. p. 19. ISBN 9788497715379.
- ↑ Mano, M. Morris and Charles R. Kime. Logic and Computer Design Fundamentals, Tercera Edición. Prentice Hall, 2004. p. 73.
Enlaces externos[editar]
- Esta obra contiene una traducción parcial derivada de «AND gate» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

