Usuario:SieirA/Sumador

Un sumador con anticipación de acarreo es un tipo de sumador usado en lógica digital. Un sumador con anticipación de acarreo mejora la velocidad reduciendo la cantidad de tiempo requerida para determinar los bits de acarreo. Puede ser contrastado con el sumador con propagación de acarreo tradicional, más simple, pero más lento, para el que el bit de acarreo se calcula junto al bit de suma, y cada bit debe esperar a que el acarreo anterior haya sido calculado para empezar a calcular su propio resultado y bit de acarreo. El sumador con anticipación de acarreo, calcula uno o más bits de acarreo antes de la suma, lo que reduce el tiempo de espera para calcular el resultado de los bits de mayor peso. Los sumadores Kogge-Stone y Brent-Kung son ejemplos de este tipo de sumador.

4-bit adder with Carry Look Ahead

Funcionamiento teórico

Un sumador con propagación de acarreo trabaja de la misma manera que los métodos de suma en papel. Empezando por el bit posicionado más a la derecha (el menos significativo), se suman los dos dígitos correspondientes y se obtiene el resultado. Es posible que haya un acarreo derivado de la suma en esta posición (por ejemplo, en suma decimal, "9+5=4, acarreo 1"). En consecuencia, todas las posiciones aparte de esta necesitan tener en cuenta la posibilidad de tener que sumar una unidad extra, proveniente del acarreo de la posición anterior.

Esto significa, que ninguna posición puede tener un valor definitivo hasta que se haya determinado si hay un acarreo o no proveniente de la derecha. Incluso, si el resultado de la suma es un 9 (en decimal) o un 1 (en binario), ni siquiera es posible determinar a priori si esta etapa va a generar un acarreo hacia la siguiente etapa a su izquierda (dado que se desconoce si habrá un acarreo proveniente de la etapa anterior). En el peor de los casos, cuando una secuencia completa de sumas llega a ser ...99999999.... (en decimal) o ...111111111... (en binario), no se puede deducir ninguno de los valores finales de los dígitos hasta que se conozca el valor del acarreo que viene desde la derecha, y en ese caso el acarreo se propaga hacia la izquierda un paso cada vez, a medida que cada posición se evalúa "9+1=0, acarreo 1" o "1+1=0, acarreo 1". Esto es la "propagación" del acarreo que da al sumador con propagación de acarreo su nombre y su lentitud.

Por ejemplo, al sumar enteros de 32 bits, se tiene que tener en cuenta la posibilidad de que el acarreo tenga que propagarse por todos y cada uno de los 32 sumadores de un bit.

La anticipación del acarreo depende de dos cosas:

1. Calcular, para cada posición de dígitos, si esta posición va a propagar un posible acarreo que viniera de las posiciones menos significativas.
2. Combinar estos valores calculados para poder deducir rápidamente si, por cada grupo de dígitos, este grupo va a propagar un acarreo que venga de la derecha.

Suponiendo que se elijan grupos de cuatro dígitos. Entonces la secuencia de eventos es algo como esto:

1. Todos los sumadores de un bit calculan sus resultados. Simultáneamente, las unidades de anticipación realizan sus cálculos
2. Suponiendo que surgiese un acarreo en un grupo particular. En un intervalo de al menos 3 retardos de puerta, ese acarreo aparecerá el en extremo izquierdo del grupo, y comenzará a propagarse a través del grupo hacia su izquierda.
3. Si el acarreo se va a propagar hasta el siguiente grupo, la unidad anticipadora ya lo habrá deducido. En consecuencia antes de que el acarreo emerja desde el siguiente grupo la unidad de anticipación es capaz de decir inmediatamente (en un retardo de puerta) al siguiente grupo a la izquierda que va a recibir el acarreo - y, al mismo tiempo, de decirle a la siguiente unidad de anticipación que hay un acarreo en camino.

El efecto neto, es que los acarreos empiezan propagándose lentamente a través de cada grupo de 4 bits, igual que en un sistema de propagación de acarreo, pero se mueve 4 veces más rápido, saltando de una unidad de anticipación a la siguiente. Finalmente, dentro de cada grupo que recibe un acarreo, el acarreo se propaga lentamente dentro de los dígitos de ese grupo.

Cuantos más bits haya en un grupo, más compleja será la lógica de la anticipación de acarreo, y más tiempo se gastará en los "tramos lentos" de cada grupo, en lugar de en el "tramo rápido" entre los grupos (provisto por la lógica de anticipación de acarreo). Por otra parte, cuantos menos bits haya en un grupo, más grupos tendrán que atravesarse para llegar de un extremo del número al otro, y como resultado, menos aceleración se conseguirá.

Decidr el tamaño del grupo que va a ser controlado por la lógica de anticipación de acarreo requiere de un análisis detallado de los retardos de puerta y propagación para la tecnología particular que se esté usando.

Es posible tener más de un nivel de lógica de anticipación de acarreo, y esto de hecho suele hacerse. Cada unidad de anticipación de acarreo produce una señal diciendo "su viene un acarreo de la derecha, lo propagaré hacia la izquierda", y esas señales pueden combinarse de modo que cada grupo de (digamos) cuatro unidades de anticipación se convierte en parte de un "supergrupo" controlando un total de 16bits de los números sumados. La lógica de anticipación de acarreo del "supergrupo" será capaz de decir si un acarreo entrando en el supergrupo será propagado a su través, y usando esta información, es capaz de propagar acarreos de derecha a izquierda 16 veces más rápido que el propagador de acarreo simple. Con este tipo de implementación de dos niveles, un acarreo puede propagarse en primer lugar por el "tramo lento" de sumadores individuales, y entonces, al alcanzar el extremo izquierdo de su grupo, propagarse por el "tramo rápido" de la lógica de anticipación de acarreo de 4bits, entonces, al alcanzar el extremo izquierdo de su supergrupo, propagarse a través del "tramo super-rápido" de la lógica de anticipación de acarreo de 16bits.

De igual modo, los tamaños de los grupos elegidos dependen de detalles particulares de cómo de rápido se propagan las señales por las puertas lógicas, y de una puerta a otra.

Para números muy grandes (cientos o incluso miles de bits) la lógica de anticipación de acarreo no se hace más compleja, porque se pueden añadir más capas de super-grupos y super-super-grupos según sea necesario. El incremento en el número de puertas es además moderado: Si todos los grupos tienen tamaño 4, uno puede terminar con un tercio de unidades de acarreo que de sumadores. De todas formas, los "tramos lentos" de camino a los niveles más altos, empiezan a imponer una traba al sistema copleto (por ejemplo, un sumador de 256bits puede tener más de 24 retardos de puerta en su procesamiento del acarreo), y la mera transmisión física de las señales de extremo a extremo de un número largo al otro empieza a ser un problema. A estos tamaños son preferibles los sumadores con acarreo almacenado ya que no toman ningún tiempo en la propagación de acarreo.

Método de anticipación de acarreo

La lógica de anticipación de acarreo usa los conceptos generar y propagar acarreos. Aunque en el contexto de un sumador con anticipación de acarreo, es más natural pensar en generar y propagar en el contexto de la suma binaria, los conceptos son más generales que eso. En las descripciones subsiguientes, la palabra dígito puede reemplazarse por bit cuando se refiera a la suma binaria.

Se dice que la suma de dos entradas A y B genera acarreo cuando esta suma siempre acarrea, sin importar si hay un acarreo de entrada (o lo que es lo mismo, sin importar si algunos dígitos menos significados en la suma generan acarreo). Por ejemplo, en la suma decimal 52 +67, la suma de las decenas 5 y 6 genera acarreo porque el resultado acarrea a las centenas independientemente de si las unidades generan acarreo (en el ejemplo no lo hacen 2 + 7 = 9).

En el caso de la suma binaria, $A+B$ genera si, y sólo si ambos A y B son 1. Si escribimos $G(A,B)$ para representar el predicado binario que es verdadero si y sólo si $A+B$ genera acarreo, tenemos:

$G(A,B)=A\cdot B$

Se dice que la suma de dos entradas A y B propaga acarreo si la suma genera acarreo cuando hay un acarreo de entrada (o lo que es lo mismo, cuando el siguiente dígito menos significativo de la suma genera acarreo). Por ejemplo, en la suma decimal 37 + 62, la suma de las decenas 3 y 6 propaga porque el resultado generará acarreo hacia las centenas si las unidades generan acarreo (lo que en este ejemplo no sucede). Nótese que propagar y generar se definen con respecto a un solo dígito de adición, y no dependen de otros dígitos de la suma.

En el caso de la suma binaria $A+B$, ésta propaga si y sólo si al menos uno de entre A y B es 1. Si escribimos $P(A,B)$ para representar el predicado binario que es cierto si y sólo si $A+B$ propaga, tenemos:

$\ P(A,B)=A+B$

A veces se usa una versión ligeramente diferente de propagar. Según esta definición se dice que A + B propagan si la suma genera un acarreo cuando hay un acarreo de entrada, pero no acarrea si no hay un acarreo de entrada. Sucede que del modo en el que se usan los bits de generación y propagación en la lógica de predicción de acarreo no importa qué definición se use. En el caso de la suma binaria, esta definición se expresa como:

$P^{\prime }(A,B)=A\oplus B$

Para la aritmética binaria, or es más rápido que xor y requiere de menos transistores en su implementación. En cualquier caso, para un sumador con predicción de acarreo multi-nivel, es más simple usar $P^{\prime }(A,B)$.

Dados estos conceptos de generar y propagar, ¿cuándo generará acarreo un dígito de una suma?. Generará el acarreo precisamente cuando bien la suma genera, o bien el siguiente bit menos significativo acarrea y la suma propaga. Escrito en álgebra booleana, con $C_{i}$ como el bit de acarreo del dígito i, y $P_{i}$ y $G_{i}$ como los bits de propagación y generación del dígito i respectivamente,

$C_{i+1}=G_{i}+\left(P_{i}\cdot C_{i}\right)$

Detalles de Implementación

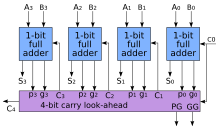
For each bit in a binary sequence to be added, the Carry Look Ahead Logic will determine whether that bit pair will generate a carry or propagate a carry. This allows the circuit to "pre-process" the two numbers being added to determine the carry ahead of time. Then, when the actual addition is performed, there is no delay from waiting for the ripple carry effect (or time it takes for the carry from the first Full Adder to be passed down to the last Full Adder). Below is a simple 4-bit generalized Carry Look Ahead circuit that combines with the 4-bit Ripple Carry Adder we used above with some slight adjustments:

For the example provided, the logic for the generate (g) and propagate (p) values are given below. Note that the numeric value determines the signal from the circuit above, starting from 0 on the far left to 3 on the far right:

$C_{1}=G_{0}+P_{0}\cdot C_{0}$

$C_{2}=G_{1}+P_{1}\cdot C_{1}$

$C_{3}=G_{2}+P_{2}\cdot C_{2}$

$C_{4}=G_{3}+P_{3}\cdot C_{3}$

Substituting $C_{1}$ into $C_{2}$, then $C_{2}$ into $C_{3}$, then $C_{3}$ into $C_{4}$ yields the expanded equations:

$C_{1}=G_{0}+P_{0}\cdot C_{0}$

$C_{2}=G_{1}+G_{0}\cdot P_{1}+C_{0}\cdot P_{0}\cdot P_{1}$

$C_{3}=G_{2}+G_{1}\cdot P_{2}+G_{0}\cdot P_{1}\cdot P_{2}+C_{0}\cdot P_{0}\cdot P_{1}\cdot P_{2}$

$C_{4}=G_{3}+G_{2}\cdot P_{3}+G_{1}\cdot P_{2}\cdot P_{3}+G_{0}\cdot P_{1}\cdot P_{2}\cdot P_{3}+C_{0}\cdot P_{0}\cdot P_{1}\cdot P_{2}\cdot P_{3}$

To determine whether a bit pair will generate a carry, the following logic works:

$G_{i}=A_{i}\cdot B_{i}$

To determine whether a bit pair will propagate a carry, either of the following logic statements work:

$P_{i}=A_{i}\oplus B_{i}$

$\ P_{i}=A_{i}+B_{i}$

The reason why this works is based on evaluation of $C_{1}=G_{0}+P_{0}\cdot C_{0}$. The only difference in the truth tables between ($A\oplus B$) and ($A+B$) is when both $A$ and $B$ are 1. However, if both $A$ and $B$ are 1, then the $G_{0}$ term is 1 (since its equation is $A\cdot B$), and the $P_{0}\cdot C_{0}$ term becomes irrelevant. The XOR is used normally within a basic full adder circuit; the OR is an alternate option (for a carry lookahead only) which is far simpler in transistor-count terms.

The Carry Look Ahead 4-bit adder can also be used in a higher-level circuit by having each CLA Logic circuit produce a propagate and generate signal to a higher-level CLA Logic circuit. The group propagate ($PG$) and group generate ($GG$) for a 4-bit CLA are:

$PG=P_{0}\cdot P_{1}\cdot P_{2}\cdot P_{3}$

$GG=G_{3}+G_{2}\cdot P_{3}+G_{1}\cdot P_{3}\cdot P_{2}+G_{0}\cdot P_{3}\cdot P_{2}\cdot P_{1}$

Putting 4 4-bit CLAs together yields four group propagates and four group generates. A Lookahead Carry Unit (LCU) takes these 8 values and uses identical logic to calculate $C_{i}$ in the CLAs. The LCU then generates the carry input for each of the 4 CLAs and a fifth equal to $C_{16}$.

The calculation of the gate delay of a 16-bit adder (using 4 CLAs and 1 LCU) is not as straight forward as the ripple carry adder. Starting at time of zero:

• calculation of $P_{i}$ and $G_{i}$ is done at time 1
• calculation of $C_{i}$ is done at time 3
• calculation of the $PG$ is done at time 2
• calculation of the $GG$ is done at time 3
• calculation of the inputs for the CLAs from the LCU are done at
  • time 0 for the first CLA
  • time 5 for the second CLA
  • time 5 for the third & fourth CLA
• calculation of the $S_{i}$ are done at
  • time 4 for the first CLA
  • time 8 for the second CLA
  • time 8 for the third & fourth CLA
• calculation of the final carry bit ($C_{16}$) is done at time 5

The maximum time is 8 gate delays (for $S_{[8-15]}$). A standard 16-bit ripple carry adder would take 31 gate delays.

Manchester carry chain

The Manchester carry chain is a variation of the carry look-ahead adder that uses shared logic to lower the transistor count. As can be seen above in the implementation section, the logic for generating each carry contains all of the logic used to generate the previous carries. A Manchester carry chain generates the intermediate carries by tapping off nodes in the gate that calculates the most significant carry value. Not all logic families have these internal nodes, however, CMOS being a major example. Dynamic logic can support shared logic, as can transmission gate logic. One of the major downsides of the Manchester carry chain is that the capacitive load of all of these outputs, together with the resistance of the transistors causes the propagation delay to increase much more quickly than a regular carry look-ahead. A Manchester carry chain section generally won't exceed 4 bits.