Teorema del transporte de Reynolds
El teorema de transporte de Reynolds es un teorema fundamental utilizado en la formulación de las leyes básicas de la mecánica de fluidos,[1] que relaciona la derivada lagrangiana de una integral de volumen de un sistema con una integral en derivadas eulerianas.[2]
Introducción[editar]
En la descripción de un fenómeno es posible elegir dos sistemas de referencia, uno centrado en una partícula por elemento de fluido (descripción lagrangiana) y un sistema inercial centrado en una posición fija en el espacio (descripción euleriana). El teorema del transporte de Reynolds establece una relación entre la variación en el espacio y en el tiempo de cualquier variable entre estos dos sistemas de referencia.
La derivada material permite evaluar la aceleración de una partícula de fluido que en un determinado instante pasa por un punto fijo del espacio.
Si, en lugar de considerar una sola partícula de fluido, se toma un sistema de fluidos, un conjunto de partículas, se tiene un problema idéntico al anterior, pero para un sistema finito en lugar de uno initesimal: el teorema de transporte de Reynolds permite relacionar las cantidades calculadas para un sistema compuesto por las mismas partículas con las calculadas para un volumen fijo en el espacio.[3]
En cálculo diferencial, el teorema de transporte de Reynolds, también conocido como teorema de transporte de Leibniz-Reynolds, o simplemente el teorema de Reynolds, llamado así por Osborne Reynolds, es una generalización tridimensional de la regla integral de Leibniz. Se utiliza para refundir las derivadas temporales de las cantidades integradas y es útil para formular las ecuaciones básicas de la mecánica del continuo. Este teorema es una expresión matemática que se usa para relacionar integrales y derivadas.
Se utiliza en la mecánica de medios continuos porque relaciona cómo varían las propiedades de una masa de control (cantidad de material a la que hacemos un seguimiento) con cómo varían las propiedades de un volumen de control (entidades geométricas que definimos aparte de los objetos físicos).
En otras palabras, este teorema relaciona la tasa de cambio en el tiempo de una propiedad extensiva con la generación y el flujo de la propiedad intensiva correspondiente , una y otra relacionadas por la ecuación. Es decir, relaciona el ritmo de variación en un dominio móvil (el de la masa de control) y un dominio fijo (el del volumen de control) o incluso entre varios volúmenes móviles.[4]
Se utiliza, por ejemplo, para demostrar la ecuación de continuidad en forma indefinida de los sistemas para cada evolución dinámica.
El teorema proporciona un medio para determinar la tasa de cambio de alguna cantidad de interés (por ejemplo, la masa o el momento lineal) tras el movimiento. Esto es lo que se necesita para transformar un principio básico de un sistema basado en la materia a uno formulado en términos de coordenadas espaciales más convenientes.[2]
Para los movimientos no estacionarios, el teorema de Reynolds también puede aplicarse a los tubos de flujo con una sección transversal no constante. Por consiguiente, no se puede tomar una sección de la tubería como volumen de control. No obstante, el problema puede resolverse refiriéndose a una sección de tubería de longitud infinita, considerando un volumen de control fijo en el tiempo.[3]
Teorema[editar]
La expresión general de este teorema es:
Demostración[editar]
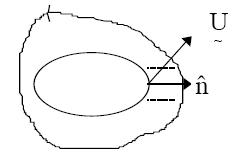
- Consideremos un sistema en dos instantes de tiempo y . Sea alguna propiedad por unidad de volumen. El sistema puede tener un cambio de volumen y posición como se muestra en la figura:
- La cantidad total de la propiedad en el sistema en el instante t es:
- Y la cantidad de α en el instante es:
- La derivada material de la cantidad total de α en el sistema se puede expresar:
- Que se obtiene de la definición de derivada:
- En esta ecuación:
- Se representa el integrando fijo con cambio de volumen como se muestra en la figura:
- Y estas dos integrales se pueden reducir a:
- Si consideramos que un elemento dS de la superficie del sistema tiene dos posiciones diferentes en los dos instantes de tiempo considerados t y t+ , el barrido de ésta superficie entre los dos instantes conforma el elemento de volumen dV como se muestra en la figura:
- Si es el vector normal a la superficie y representa la velocidad, será la velocidad normal a la superficie. En el tiempo la superficie se mueve una distancia normal a la misma. Por lo que:
- La integral se reduce a la integral sobre la superficie:
- Tomando el límite se simplifica a:
- Aplicando el teorema de Gauss esta integral toma la forma:
- Dos términos de la ecuación pueden simplificarse como:
- Con estas simplificaciones toma la forma:
- En notación indical:
El lema de Reynolds[editar]
El lema de Reynolds introducido por el ingeniero irlandés Osborne Reynolds que demuestra que la variación de flujo de una propiedad es igual a la variación de la propiedad dentro del flujo:
Demostración[editar]
Sea A una cierta propiedad genérica (escalar, vectorial o tensorial) de un medio continuo, y sea ψ(x, t) la cantidad de esta propiedad A por unidad de masa. Por consiguiente, ρψ(x, t) es la cantidad de la propiedad por unidad de volumen.
Consideremos un volumen material arbitrario de medio continuo que en el
instante t ocupa en el espacio un volumen V. La cantidad de la propiedad
genérica A en el volumen material V en el instante t será:
Donde ψ es la propiedad a estudiar
La variación a lo largo del tiempo del contenido de la propiedad A en el volumen material V vendrá dada por la derivada temporal de Q(t) , que utilizando la expresión de la derivada material de una integral de volumen será:
Utilizando la expresión para la derivada material de un producto de funciones, agrupando términos y utilizando la ecuación de continuidad:
Como por continuidad, se llega a la conclusión de que:
Referencias[editar]
- ↑ O. Reynolds, Papers on mechanical and physical subjects-the sub-mechanics of the Universe, Collected Work, Volume III, Cambridge University Press, 1903.
- ↑ a b «ME6601 Module Six - Reynolds Transport Theorem». web.archive.org. 27 de marzo de 2008. Archivado desde el original el 27 de marzo de 2008. Consultado el 27 de febrero de 2022.
- ↑ a b «Dinamica dei fluidi».
- ↑ «Teorema del transporte de Reynolds - SGCG». sgcg.es. Consultado el 27 de febrero de 2022.

























![{\displaystyle \lim _{\delta t\to 0}{\frac {1}{\delta t}}\left[\int \limits _{V(t)}\alpha (t+\delta t)dV-\int \limits _{V(t)}\alpha (t)dV\right]=\int \limits _{V(t)}\lim _{\delta t\to 0}{\frac {1}{\delta t}}\left[\alpha (t+\delta t)-\alpha (t)\right]dV=\int \limits _{V(t)}{\frac {\partial \alpha }{\partial t}}dV}](https://wikimedia.org/api/rest_v1/media/math/render/svg/332ffd2e172d13efff1fad0f9a92254ca592efa4)
![{\displaystyle {\frac {D}{Dt}}\int \limits _{V(t)}\alpha (t)dV=\int \limits _{V(t)}\left[{\frac {\partial \alpha }{\partial t}}+\nabla \cdot (\alpha {\vec {U}})\right]dV}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c293315e613a6e9c0392b2ad26a2f2e26157b4cd)
![{\displaystyle {\frac {D}{Dt}}\int \limits _{V(t)}\alpha (t)dV=\int \limits _{V(t)}\left[{\frac {\partial \alpha }{\partial t}}+{\frac {\partial (\alpha u_{i})}{\partial x_{i}}}\right]dV}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3b7f462426aecf0bc92b3c02e31176e3a674e67)


![{\displaystyle \ Q'(t)={\frac {d}{dt}}\int _{V_{f}(t)}\rho \Psi \;d\ V=\int _{V_{f}(t)}\left[{\frac {d\rho \psi }{dt}}\ +\rho \psi \nabla \cdot \ v\right]\;d\ V}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fab1aabfb72e3c696d27397568980ccf26cbd20)
![{\displaystyle {\frac {d}{dt}}\int _{V_{f}(t)}\rho \Psi \;d\ V=\int _{V_{f}(t)}\left[\rho {\frac {d\psi }{dt}}\ +\psi {\frac {d\rho }{dt}}+\rho \psi \nabla \cdot \ v\right]\;d\ V}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9a540de78c7899719f6e74872650a4593ab1a9d)
![{\displaystyle =\int _{V_{f}(t)}\left[\rho {\frac {d\psi }{dt}}\ +\psi \left[{\frac {d\rho }{dt}}+\rho \nabla \cdot \ v\right]\right]\;d\ V}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88a36e096099e3a6fc2830bba60a8b98eca6a600)
