Teorema de Kuratowski
En teoría de grafos, el teorema de Kuratowski, desarrollado por el matemático polaco Kazimierz Kuratowski, es una caracterización de los grafos planares.
Definición
[editar]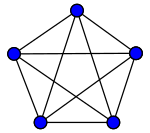
|
Una subdivisión elemental de un grafo resulta de insertar vértices en las aristas (por ejemplo, cambiando •——• por •—•—•). Una formulación equivalente a este teorema es:
|
Ejemplo
[editar]
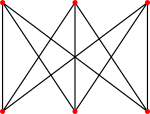
¿El grafo K6 completo puede ser plano?
Si se elimina un vértice de K6 y todas las aristas que lo unen con el resto de vértices, se puede observar que el grafo K6 contiene como subgrafo un K5. Por el Teorema de Kuratowski se puede afirmar que el grafo K6 no es planar.
