Simulación Barnes-Hut

La simulación Barnes-Hut (Josh Barnes y Piet Hut) es un algoritmo para realizar una simulación de n-cuerpos. Se destaca por tener un orden O(n log n) en comparación con un algoritmo de suma directa que sería O(n²).

Una simulación 100-cuerpo con el árbol de Barnes-Hut visualmente como cajas azules.

El volumen de la simulación está generalmente dividido en células cúbicas a través de un octree (en un espacio tridimensional), de manera que solo las partículas de las células cercanas necesitan ser tratadas individualmente, y las partículas en células distantes puede ser tratadas como una sola partícula grande centrada en el centro de la célula (o como de orden inferior desarrollo multipolar ). Esto puede reducir drásticamente el número de interacciones entre pares de partículas que deben ser calculadas.

Algoritmo

Árbol Barnes-Hut

En una simulación de N-cuerpos tridimensional, el algoritmo Barnes-Hut divide recursivamente los N cuerpos en grupos, almacenándolos en un octree (o en un quadtree en una simulación 2D). Cada nodo en este árbol representa una región del espacio tridimensional. El nodo superior representa todo el espacio, y sus ocho hijos representan los ocho octantes del espacio, cada uno de los cuales se pueden dividir nuevamente en ocho octantes. El espacio se subdivide en octantes de forma recursiva hasta que cada subdivisión contiene 0 o 1 cuerpos (algunas regiones no tienen cuerpos en todos sus cuadrantes). Hay dos tipos de nodos en un octree: nodos internos y externos. Un nodo externo no tiene hijos, y está vacío o representa un solo cuerpo. Cada nodo interno representa un grupo de cuerpos contenidos en su interior, y almacena el centro de la masa y la masa total de todos los cuerpos hijos.

• 
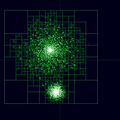
  Distribución de partículas que se asemeja a la de dos galaxias vecinas
• 
  Árbol Barnes-Hut completo. (Los nodos que no contienen partículas no están dibujados)
• 
  Los nodos del árbol Barnes-Hut utilizados para calcular la fuerza que actúa sobre una partícula situada en el origen.
• Simulación de N-cuerpos basada en el algoritmo Barnes-Hut.

Cálculo de la fuerza que actúa sobre un cuerpo

Para calcular la fuerza neta sobre un cuerpo en particular, los nodos del árbol son recorridos desde la raíz. Si el centro de masas de un nodo interno está lo suficientemente lejos del cuerpo, los cuerpos contenidos en esa parte del árbol se tratan como un solo cuerpo, cuya posición y masa son, respectivamente, el centro de masa y la masa total del nodo interno. Si el nodo interno no está lo suficientemente lejos del cuerpo, el proceso se repite para cada una de sus ramificaciones.

Si un nodo está o no lo suficientemente lejos de un cuerpo, depende del cociente s / d, donde s es el ancho de la región representada por el nodo interno, y d es la distancia entre el cuerpo y el centro de masas del nodo. El nodo está suficientemente lejos cuando esta relación es menor que un valor umbral θ. El parámetro θ determina la exactitud de la simulación, valores más grandes de θ aumentan la velocidad de la simulación, pero disminuyen su exactitud. Si θ = 0, ningún nodo interno es tratado como un solo cuerpo y el algoritmo degenera a un algoritmo de suma directa.

Referencias

• J. Barnes and P. Hut (diciembre de 1986). «A hierarchical O(N log N) force-calculation algorithm». Nature 324 (4): 446-449. doi:10.1038/324446a0. 
• J. Dubinski (octubre de 1996). «A Parallel Tree Code». New Astronomy 1 (2): 133-147. doi:10.1016/S1384-1076(96)00009-7. arΧiv:astro-ph/9603097v1. 
• U. Becciani, R. Ansalonib, V. Antonuccio-Delogua, G. Erbaccic, M. Gamberaa, and A. Pagliarod (octubre de 1997). «A parallel tree code for large N-body simulation: dynamic load balance and data distribution on a CRAY T3D system». Computer Physics Communications 106 (1–2): 105-113. doi:10.1016/S0010-4655(97)00102-1. 
• T. Ventimiglia, and K. Wayne. «The Barnes-Hut Algorithm». Consultado el 30 de marzo de 2012. 

• Datos: Q808453