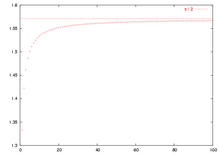
Gráfico del desarrollo parcial del producto de Wallis. En matemáticas , se conoce como producto de Wallis una expresión utilizada para representar el valor de π que fue descubierta por John Wallis en 1655 y que establece que:
∏
n
=
1
∞
(
2
n
2
n
−
1
⋅
2
n
2
n
+
1
)
=
2
1
⋅
2
3
⋅
4
3
⋅
4
5
⋅
6
5
⋅
6
7
⋅
8
7
⋅
8
9
⋯
=
π
2
{\displaystyle \prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots ={\frac {\pi }{2}}}
Demostración [ editar ] Antes que nada se debe considerar que las raíces de sen(x)/x son ±nπ, donde n = 1, 2, 3.... Entonces, se puede expresar el seno como un producto infinito de factores lineales de sus raíces:
sen
(
x
)
x
=
k
(
1
−
x
π
)
(
1
+
x
π
)
(
1
−
x
2
π
)
(
1
+
x
2
π
)
(
1
−
x
3
π
)
(
1
+
x
3
π
)
⋯
donde
k
es~una~constante
{\displaystyle {\frac {\operatorname {sen}(x)}{x}}=k\left(1-{\frac {x}{\pi }}\right)\left(1+{\frac {x}{\pi }}\right)\left(1-{\frac {x}{2\pi }}\right)\left(1+{\frac {x}{2\pi }}\right)\left(1-{\frac {x}{3\pi }}\right)\left(1+{\frac {x}{3\pi }}\right)\cdots \qquad \ {\textrm {donde}}~k~{\textrm {es~una~constante}}}
Para encontrar la constante k, se toma el límite en ambos lados:
lim
x
→
0
sen
(
x
)
x
=
lim
x
→
0
(
k
(
1
−
x
π
)
(
1
+
x
π
)
(
1
−
x
2
π
)
(
1
+
x
2
π
)
(
1
−
x
3
π
)
(
1
+
x
3
π
)
⋯
)
=
k
{\displaystyle \lim _{x\to 0}{\frac {\operatorname {sen}(x)}{x}}=\lim _{x\to 0}\left(k\left(1-{\frac {x}{\pi }}\right)\left(1+{\frac {x}{\pi }}\right)\left(1-{\frac {x}{2\pi }}\right)\left(1+{\frac {x}{2\pi }}\right)\left(1-{\frac {x}{3\pi }}\right)\left(1+{\frac {x}{3\pi }}\right)\cdots \right)=k}
Sabiendo que:
lim
x
→
0
sen
(
x
)
x
=
1
{\displaystyle \lim _{x\to 0}{\frac {\operatorname {sen}(x)}{x}}=1}
Se hace k=1. Obtenemos la fórmula de Euler-Wallis para el seno:
sen
(
x
)
x
=
(
1
−
x
π
)
(
1
+
x
π
)
(
1
−
x
2
π
)
(
1
+
x
2
π
)
(
1
−
x
3
π
)
(
1
+
x
3
π
)
⋯
{\displaystyle {\frac {\operatorname {sen}(x)}{x}}=\left(1-{\frac {x}{\pi }}\right)\left(1+{\frac {x}{\pi }}\right)\left(1-{\frac {x}{2\pi }}\right)\left(1+{\frac {x}{2\pi }}\right)\left(1-{\frac {x}{3\pi }}\right)\left(1+{\frac {x}{3\pi }}\right)\cdots }
sen
(
x
)
x
=
(
1
−
x
2
π
2
)
(
1
−
x
2
4
π
2
)
(
1
−
x
2
9
π
2
)
⋯
{\displaystyle {\frac {\operatorname {sen}(x)}{x}}=\left(1-{\frac {x^{2}}{\pi ^{2}}}\right)\left(1-{\frac {x^{2}}{4\pi ^{2}}}\right)\left(1-{\frac {x^{2}}{9\pi ^{2}}}\right)\cdots }
Haciendo x=π/2, se obtiene:
1
π
/
2
=
(
1
−
1
2
2
)
(
1
−
1
4
2
)
(
1
−
1
6
2
)
⋯
=
∏
n
=
1
∞
(
1
−
1
4
n
2
)
{\displaystyle {\frac {1}{\pi /2}}=\left(1-{\frac {1}{2^{2}}}\right)\left(1-{\frac {1}{4^{2}}}\right)\left(1-{\frac {1}{6^{2}}}\right)\cdots =\prod _{n=1}^{\infty }\left(1-{\frac {1}{4n^{2}}}\right)}
π
2
=
∏
n
=
1
∞
(
4
n
2
4
n
2
−
1
)
{\displaystyle {\frac {\pi }{2}}=\prod _{n=1}^{\infty }\left({\frac {4n^{2}}{4n^{2}-1}}\right)}
=
∏
n
=
1
∞
(
2
n
2
n
−
1
⋅
2
n
2
n
+
1
)
=
2
1
⋅
2
3
⋅
4
3
⋅
4
5
⋅
6
5
⋅
6
7
⋯
{\displaystyle =\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdots }
Enlaces externos [ editar ]