Modelo Booleano Extendido
El Modelo Booleano Extendido fue presentado en un artículo de Communications of the ACM en el año 1983, por Gerard Salton, Edward A. Fox y Harry Wu. El propósito del Modelo Booleano Extendido es superar las desventajas del Modelo Booleano que ha sido utilizado en recuperación de información. El Modelo Booleano no considera los pesos de los términos en las consultas y el conjunto respuesta de una consulta booleana es con frecuencia demasiado pequeño o demasiado grande. La idea del modelo extendido es hacer uso de la correspondencia parcial y los pesos de los términos del Modelo de Espacio Vectorial, combinándolos con las propiedades del Álgebra Booleana. De esta forma, un documento puede ser un tanto relevante si contiene algunos términos de la consulta, y puede ser obtenido como respuesta, mientras que en el Modelo Booleano esto no ocurre.[1]
Así, el Modelo Booleano Extendido puede ser considerado como una generalización de los modelos Booleano y Vectorial. Además, la investigación ha demostrado mejoras en la efectividad respecto al procesamiento de consultas del Modelo Booleano. Otras investigaciones han mostrado que la retroalimentación y la expansión de consultas pueden ser adaptadas al procesamiento de consultas del Modelo Booleano Extendido.
Definiciones
[editar]En el Modelo Booleano Extendido un documento se representa por un vector (al igual que en el Modelo Vectorial). Cada componente corresponde a un término asociado al documento.
El peso del término asociado al documento se mide por su frecuencia de término normalizada y puede definirse como:
donde es la frecuencia inversa de documento.
El vector de pesos asociado al documento puede ser representado como:
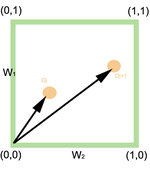
Ejemplo en 2 Dimensiones
[editar]Considerando el espacio compuesto por los dos términos y , los pesos correspondientes son y .[2] Así, para la consulta , podemos calcular la similitud con la siguiente fórmula:
Para la consulta , podemos usar:
Generalizando la idea
[editar]Podemos generalizar el ejemplo anterior en 2 dimensiones del Modelo Booleano Extendido al espacio t-dimensional usando la distancia Euclidiana.
Esto puede hacerse usando Norma-P, que extiende la noción de distancia para incluir p-distancias, donde es un nuevo parámetro.[3]
- Una consulta conjuntiva general está dada por:
La similitud de la consulta y el documento puede definirse como:
- Una consulta disyuntiva general está dada por:
La similitud de la consulta y el documento puede definirse como:
Ejemplos
[editar]Considere la consulta . La similitud entre la consulta y el documento puede calcularse usando la fórmula:
Mejoras respecto al Modelo Booleano
[editar]Lee y Fox[4] compararon los modelos Booleano y Booleano Extendido con tres colecciones de prueba, CISI, CACM e INSPEC.
Utilizando Norma-P se obtuvo un promedio de mejoras en la precisión de 79%, 106% y 210% respecto al Modelo Booleano estándar, para las colecciones CISI, CACM e INSPEC, respectivamente.
El modelo de Norma-P es computacionalmente costoso por el número de operaciones de exponenciación que requiere; sin embargo, logra resultados mucho mejores que el Modelo Booleano, e incluso que el Modelo Fuzzy. El Modelo Booleano estándar es, no obstante, el más eficiente.
Véase también
[editar]Bibliografía
[editar]- ↑ Salton, Gerard; Edward A. Fox, Harry Wu (1983), Extended Boolean information retrieval, Communications of the ACM, Volume 26, Issue 11 .
- ↑ Lusheng Wang
- ↑ Garcia, Dr. E., The Extended Boolean Model - Weighted Queries: Term Weights, p-Norm Queries and Multiconcept Types. Boolean OR Extended? AND that is the Query, archivado desde el original el 29 de mayo de 2010.
- ↑ Lee, W. C.; E. A. Fox (1988), Experimental Comparison of Schemes for Interpreting Boolean Queries .
Enlaces externos
[editar]- Esta obra contiene una traducción derivada de «Extended Boolean model» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.





![{\displaystyle \mathbf {v} _{d_{j}}=[w_{1,j},w_{2,j},\ldots ,w_{i,j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7630d41a2858849a4a1998c1a7bf46c90a18d7cc)














![{\displaystyle sim(q_{or},d_{j})={\sqrt[{p}]{\frac {w_{1}^{p}+w_{2}^{p}+....+w_{t}^{p}}{t}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ee6fd28a0b708483aa6ff23a382886234751498)


![{\displaystyle sim(q_{and},d_{j})=1-{\sqrt[{p}]{\frac {(1-w_{1})^{p}+(1-w_{2})^{p}+....+(1-w_{t})^{p}}{t}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8a46594acad810a7ec2e9e62a712b694fb18916)



![{\displaystyle sim(q,d)={\sqrt[{p}]{\frac {(1-{\sqrt[{p}]{({\frac {(1-w_{1})^{p}+(1-w_{2})^{p}}{2}}}}))^{p}+w_{3}^{p}}{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74b3d2b11ee65d16df85d7d45087259d37a10215)