Diferencia entre revisiones de «Método de la secante»
m Bot: Poniendo punto a descripción de imagen; cambios cosméticos |
|||
| Línea 12: | Línea 12: | ||
== Derivación del método == |
== Derivación del método == |
||
El método se basa en obtener la ecuación de la recta que pasa por los puntos (''x''<sub>''n''−1</sub>, ''f''(''x''<sub>''n''−1</sub>)) y (''x''<sub>''n''</sub>, ''f''(''x''<sub>''n''</sub>)). A dicha recta se le llama ''secante'' por cortar la gráfica de la función. Posteriormente se escoge como siguiente elemento de la relación de recurrencia, ''x''<sub>''n''+1</sub>, la intersección de la recta secante con el eje de abscisas obteniendo la fórmula. |
El método se basa en obtener la ecuación de la recta que pasa por los puntos (''x''<sub>''n''−1</sub>, ''f''(''x''<sub>''n''−1</sub>)) y (''x''<sub>''n''</sub>, ''f''(''x''<sub>''n''</sub>)). A dicha recta se le llama ''secante'' por cortar la gráfica de la función. Posteriormente se escoge como siguiente elemento de la relación de recurrencia, ''x''<sub>''n''+1</sub>, la intersección de la recta secante con el eje de abscisas obteniendo la fórmula. |
||
el soe se la come |
|||
rico |
|||
== Convergencia == |
== Convergencia == |
||
Revisión del 14:21 26 abr 2010
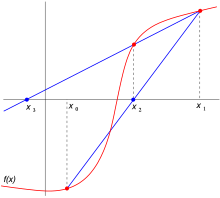
En análisis numérico el método de la secante es un método para encontrar los ceros de una función de forma iterativa.
Es una variación del método de Newton-Raphson donde en vez de calcular la derivada de la función en el punto de estudio, teniendo en mente la definición de derivada, se aproxima la pendiente a la recta que une la función evaluada en el punto de estudio y en el punto de la iteración anterior. Este método es de especial interés cuando el coste computacional de derivar la función de estudio y evaluarla es demasiado elevado, por lo que el método de Newton no resulta atractivo.
El método
El método se define por la relación de recurrencia:
Como se puede ver, este método necesitará dos aproximaciones iniciales de la raíz para poder inducir una pendiente inicial.
Derivación del método
El método se basa en obtener la ecuación de la recta que pasa por los puntos (xn−1, f(xn−1)) y (xn, f(xn)). A dicha recta se le llama secante por cortar la gráfica de la función. Posteriormente se escoge como siguiente elemento de la relación de recurrencia, xn+1, la intersección de la recta secante con el eje de abscisas obteniendo la fórmula. el soe se la come
rico
Convergencia
El orden de convergencia de este método, en un punto cercano a la solución, es donde
es el número áureo, por lo que se trata de una convergencia superlineal inferior a la del método de Newton-Raphson. En caso de que la aproximación inicial sea demasiado lejana o la raíz no sea simple, este método no asegura la convergencia y tiene un comportamiento similar al de Newton-Raphson.
Enlaces externos
- Animations for the secant method
- Secant method of zero (root) finding on Mathcad Application Server
- Secant Method Notes, PPT, Mathcad, Maple, Mathematica, Matlab at Holistic Numerical Methods Institute
- Module for Secant Method by John H. Mathews



