Método de distribución de momentos
El Método de redistribución de momentos o método de Cross[1] es un método de análisis estructural para vigas estáticamente indeterminadas y marcos/pórticos planos, desarrollado por Hardy Cross y que permitía el cálculo de estructuras hiperestáticas mediante un método iterativo que convergía hacia la solución correcta.
El método fue publicado en 1930 en una revista de la ASCE. El método solo calcula el efecto de los momentos flectores e ignora los efectos axiales y cortantes, lo cual es suficiente para fines prácticos en barras esbeltas. Desde 1930 hasta que las computadoras comenzaron a ser ampliamente usadas en el diseño y análisis de estructuras, el método de redistribución de momentos fue el más usado en la práctica. Posteriormente otros métodos como el método matricial de la rigidez que se puede programar de manera más sencilla han llegado a ser más populares que el método de redistribución de momentos de Cross.
Introducción[editar]
En el método de redistribución de momentos, cada articulación o nodo de la estructura, se considera fija en una primera fase a fin de desarrollar los Momentos en los Extremos Fijos. Después cada articulación fija se considera liberada secuencialmente y el momento en el extremo fijo (el cual al momento de ser liberado no está en equilibrio) se "distribuye" a miembros adyacentes hasta que el equilibrio es alcanzado. El método de distribución de momentos en términos matemáticos puede ser demostrado como el proceso de resolver una serie de sistemas de ecuaciones por medio de iteración.
El método de redistribución de momentos cae dentro de la categoría de los métodos de desplazamiento del análisis estructural.
Implementación[editar]
El método de Cross es un método iterativo, tiene la ventaja de estar planteado como una sucesión de grupos de fases de cálculo, si a partir de un cierto punto se siguen repitiendo alguna de las fases de cálculo ("transmisión" y "reparto" de momentos) la solución va convergiendo hacia la solución exacta. Esto era muy importante en las primeras décadas de uso del método, cuando no existían ordenadores disponibles para el cálculo estructural. La llegada de ordenadores y la existencia de algoritmos eficientes para resolución de sistemas con un elevado número de ecuaciones, hicieron aparecer alternativas al método de Cross que al menos hasta los años 1960, fue el principal método de cálculo. En la actualidad la mayor parte del software estructural usa el método matricial de la rigidez, que es más sencillo de programar.
Hardy Cross no desarrolló una versión tridimensional de su método, por lo que en gran parte el método se empleó para estructuras planas. Aunque añadiendo la noción de rigidez torsional es generalizable a tres dimensiones. El método de Cross puede dividirse en una serie fases o etapas de cálculo (siendo las últimas de ellas reiterables, hasta obtener la precisión deseada). La etapas son:
- Etapa previa de cálculo de los momentos de empotramiento fijos, así como cálculo de los coeficientes de transmisión y distribución. Esta etapa se realiza sólo una vez.
- Etapa de distribución de momentos, dentro de cada nudo se suman todos los momentos aplicados, cuando la suma no es cero el nudo estará desequilibrado y será necesario producir un giro que deformará los elementos estructurales convergentes a dicho nudo. Tras la aparición de giros y deformaciones aparecerán momentos elásticos que deben calcularse. Estos se calculan "repartiendo" o distribuyendo el momento de desequilibrio entre las barras de acuerdo a los coeficientes de reparto que dependen de las rigideces relativas. El elemento más rígido es que el que asumirá la mayor parte del momento de desequilibrio. A esta fase le sigue siempre la fase de transmisión de momentos.
- Etapa de transmisión de momentos, una vez planteado el equilibrio parcial de los nudos mediante la aparición de fuerzas elásticas que se oponen a los giros, debe tenerse en cuenta que en cada barra no se puede deformar un nudo extremo sin que el otro sufra una variación de esfuerzos. El cálculo de esas variaciones es la llamada transmisión de esfuerzos, a partir de lo momento repartidos en la fase anterior es necesario ver que momentos inducen en los nudos conectados por vigas o pilares. Estos nuevos momentos se denominan momentos transmitidos.
La nueva transmisión de momentos hace que aparezcan nuevos desequilibrios en los nudos que deben repartirse de nuevo y volver a la etapa 2. Una virtud del método es que al ir repitiendo las fases 2 y 3, en cada iteración los momentos son sustancialmente menores (al ser los coeficientes de reparto y transmisión menores que la unidad) y se logra convergencia en términos prácticos después de un número relativamente bajo de iteraciones.
En disposición de aplicar el método de redistribución de momentos para analizar una estructura, lo siguiente debe ser considerado.
Momentos de empotramiento en extremos fijos[editar]
Momentos de empotramiento en extremos fijos son los momentos producidos al extremo del miembro por cargas externas cuando las juntas están fijas.
Rigidez a la flexión[editar]
La rigidez a la flexión es la propiedad que tiene un elemento que le permite resistir un límite de esfuerzos de flexión sin deformarse. La rigidez flexional (EI/L) de un miembro es representada como el producto del módulo de elasticidad (E) y el segundo momento de área, también conocido como Momento de Inercia (I) dividido por la longitud (L) del miembro, que es necesaria en el método de distribución de momentos, no es el valor exacto pero es la Razón aritmética de rigidez de flexión de todos los miembros.
Coeficientes de distribución[editar]
Los coeficientes de distribución pueden ser definidos como las proporciones de los momentos no equilibrados que se distribuyen a cada uno de los miembros. Un momento no equilibrado en un nudo, es distribuido a cada miembro concurrente en él, esta distribución se hace directamente proporcional a la rigidez a la flexión que presenta cada uno de estos miembros.
Coeficientes de transmisión[editar]
Los momentos no equilibrados son llevados sobre el otro extremo del miembro cuando se permite el giro en el apoyo. La razón de momento acarreado sobre el otro extremo entre el momento en el extremo fijo del extremo inicial es el coeficiente de transmisión.
- -Valores típicos:
- 0 para nodos sin empotramiento
- 0,5 para nodos empotrados
Convención de signos[editar]
Un momento actuando en sentido horario es considerado positivo. Esto difiere de la [convención de signos] usual en ingeniería, la cual emplea un sistema de coordenadas cartesianas con el eje positivo X a la derecha y el eje positivo Y hacia arriba, resultando en momentos positivos sobre el eje Z siendo antihorarios.
Estructuras de marcos[editar]
Estructuras de marcos con o sin ladeo pueden ser analizadas utilizando el método de distribución de momentos.
Ejemplo[editar]
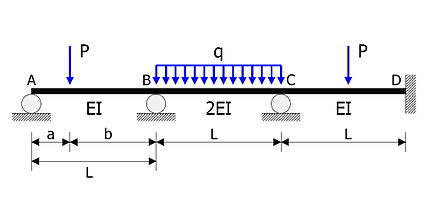
La viga estáticamente indeterminada mostrada en la figura será analizada.
- Miembros AB, BC, CD tienen la misma longitud .
- Las rigideces flexionales son EI, 2EI, EI respectivamente.
- Cargas concentradas de magnitud actúan a una distancia desde el soporte A.
- Carga uniforme de intensidad actúa en BC.
- Miembro CD está cargado a la mitad de su claro con una carga concentrada de magnitud .
En los siguientes cálculos, los momentos antihorarios son positivos.
Coeficientes de reparto[editar]
Los coeficientes de reparto de las juntas A y D son .
Coeficientes de transmisión[editar]
Los coeficientes de transmisión son (porque la sección es constante), excepto para el factor de acarreo desde D (soporte fijo) a C el cual es cero.
Distribución de momentos[editar]
Números en gris son momentos balanceados; flechas ( → / ← ) representan el acarreo de momento desde un extremo al otro extremo de un miembro.
Resultados[editar]
- Momentos en articulaciones, determinados por el método de distribución de momentos.
- La convención de signos usual en ingeniería es usada aquí, i.e. Los momentos positivos causan elongación en la parte inferior de un elemento de viga.
Para propósitos de comparación, los siguientes son los resultados generados, usando un método matricial. Nota que en el análisis superior, el proceso iterativo fue llevado a >0.01 de precisión. El hecho de que el resultado de análisis de matriz y el resultado de análisis de distribución de momentos iguale a 0.001 de precisión es mera coincidencia.
- Momentos en articulaciones determinados por el método matricial
Los diagramas completos de cortante y momento flector son como sigue. Nota que el método de distribución de momentos solo determina los momentos en las juntas. Desarrollando diagramas de momentos flectores completos requiere de cálculos adicionales usando los momentos determinados en las articulaciones y el equilibrio interno de la sección.
| DEC | DMF |

(Posible corrección en esfuerzo de corte 5.84 en lugar de 3.84, y -4.16 en lugar de -6.16). |

|
| Diagrama de esfuerzos cortantes. | Diagrama de momentos flectores. |
Véase también[editar]
Referencias[editar]
- ↑ Ofinalca/Santa Teresa del Tuy (7 de abril de 2012). «Teoría de estructuras II, Unidad 1, Método de Cross». Consultado el 8 de marzo de 2013.
















