Jerarquía aritmética

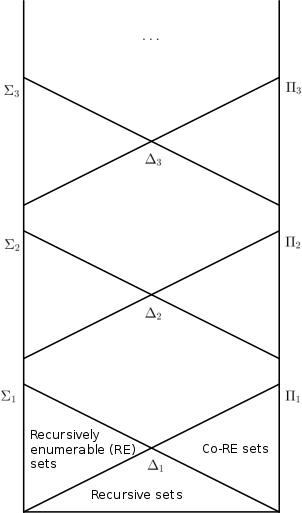
La jerarquía aritmética, o jerarquía de Kleene clasifica ciertos conjuntos basándose en la complejidad de las fórmulas que los definen. Todo conjunto que recibe una clasificación es llamado aritmético. La jerarquía aritmética es importante en la teoría de recursión, teoría de conjunto descriptivos eficientes, y el estudio de teorías formales tales como aritmética de Peano. El algoritmo de Tarski-Kuratowski da una forma fácil de obtener un límite superior sobre las clasificaciones que se asignan a una fórmula y al conjunto que la misma define.

La jerarquía hiperaritmética y la jerarquía analítica extienden la jerarquía aritmética clasificando fórmulas y conjuntos adicionales.

Jerarquía aritmética de fórmulas[editar]

La jerarquía aritmética asigna clasificaciones a las fórmulas en el lenguaje de axiomas de Peano (aritmética de primer orden). Las clasificaciones son identificadas como $\Sigma _{n}^{0}$ y $\Pi _{n}^{0}$ para números naturales n. Las letras griegas son aquí símbolos sin resaltar, que indica que las fórmulas no contienen parámetros de conjunto.

Las clasificaciones $\Sigma _{n}^{0}$ y $\Pi _{n}^{0}$ se definen en forma inductiva para todo número natural n utilizando las siguientes reglas:

Si $\phi$ es lógicamente equivalente a una fórmula sin cuantificadores, se le asigna la clasificación $\Sigma _{0}^{0}=\Pi _{0}^{0}$ .
Si $\phi$ es lógicamente equivalente a una fórmula del tipo $\exists n_{1}\cdots \exists n_{k}\psi$ , donde $\psi$ es $\Pi _{n}^{0}$ , entonces a $\phi$ se le asigna la clasificación $\Sigma _{n+1}^{0}$ .
Si $\phi$ es lógicamente equivalente a una fórmula del tipo $\forall n_{l}\cdots \forall n_{k}\psi$ , donde $\psi$ es $\Sigma _{n}^{0}$ , entonces a $\phi$ se le asigna la clasificación $\Pi _{n+1}^{0}$ .

Jerarquía aritmética de conjuntos de números naturales[editar]

Sea un conjunto X definido por la fórmula φ(n) en el lenguaje de aritmética de Peano si $n\in X\leftrightarrow \mathbb {N} \models \phi (n)$ . Lo que significa que los elementos de X son exactamente los números que satisfacen φ. Un conjunto es definible mediante aritmética de primer orden si el mismo es definido por alguna fórmula en el lenguaje de la aritmética de Peano.

A cada conjunto X de números naturales que es definible mediante aritmética de primer orden se les asignan clasificaciones del tipo $\Sigma _{n}^{0}$ , $\Pi _{n}^{0}$ , y $\Delta _{n}^{0}$ , donde $n$ es un número natural, según se indica a continuación. Si X es definible por una fórmula $\Sigma _{n}^{0}$ entonces a $X$ se le asigna la clasificación $\Sigma _{n}^{0}$ . Si X es definible por una fórmula $\Pi _{n}^{0}$ entonces a $X$ se le asigna la clasificación $\Pi _{n}^{0}$ . Si $X$ es $\Sigma _{n}^{0}$ y $\Pi _{n}^{0}$ entonces a $X$ se le asigna la clasificación adicional $\Delta _{n}^{0}$ .

Notar que casi no tiene sentido referirse a fórmulas del tipo $\Delta _{n}^{0}$ ; el primer cuantificador de una fórmula es o bien existencial o universal. Por lo tanto un conjunto $\Delta _{n}^{0}$ no se encuentra definido por una fórmula del tipo $\Delta _{n}^{0}$ ; más bien, son las fórmulas $\Sigma _{n}^{0}$ y $\Pi _{n}^{0}$ las que definen el conjunto.
Se utiliza una definición paralela para definir la jerarquía aritmética en potencias finitas cartesianas de números naturales. En vez de fórmulas con una variable libre, se utilizan fórmulas con k variables libres para definir la jerarquía aritmética sobre conjuntos de k-tuplos de números naturales.
Jerarquías aritméticas relativizadas
De la misma manera como se puede definir que es lo que significa que un conjunto X sea recursivo con relación a otro conjunto Y permitiendo que el cálculo que define a X consulte a Y como si fuera un oráculo, podemos extender este concepto a toda la jerarquía aritmética y definir lo que significa que X sea $\Sigma _{n}^{0}$ , $\Delta _{n}^{0}$ o $\Pi _{n}^{0}$ en Y, lo que se indica respectivamente como $\Sigma _{n}^{0,Y}$ $\Delta _{n}^{0,Y}$ y $\Pi _{n}^{0,Y}$ . Para hacer esto fijamos un conjunto de enteros Y y sumamos un predicado de pertenencia en Y al lenguaje de la aritmética de Peano. Luego afirmamos que X se encuentra en $\Sigma _{n}^{0,Y}$ si está definido por una fórmula $\Sigma _{n}^{0}$ en este lenguaje expandido. Es decir, X es $\Sigma _{n}^{0,Y}$ si se encuentra definido por una fórmula $\Sigma _{n}^{0}$ que está habilitada a formular preguntas sobre pertenencia en Y. Alternativamente, se pueden interpretar los conjuntos $\Sigma _{n}^{0,Y}$ como aquellos conjuntos que pueden ser construidos comenzando a partir de conjuntos recursivos en Y y alternativamente proyectando y tomando complementos de estos conjuntos hasta n veces.
Por ejemplo sea Y un conjunto de enteros. Y sea X el conjunto de números enteros divisibles por un elemento de Y. Entonces X queda definida por la fórmula $\phi (n)=\exists m\exists t(Y(m)\land m\times t=n)$ por lo que X se encuentra en $\Sigma _{1}^{0,Y}$ (en realidad se encuentra también en $\Delta _{0}^{0,Y}$ dado que podemos acotar ambos cuantificadores con n).

Reducibilidad y grados de la aritmética[editar]

La reducibilidad aritmética es un concepto intermedio entre la reducibilidad de Turing y la reducibilidad hiperaritmética. Un conjunto es aritmético (o definible aritméticamente) si es definido por alguna fórmula en el lenguaje de aritmética de Peano. En forma equivalente se dice que X es aritmético si X es $\Sigma _{n}^{0}$ o $\Pi _{n}^{0}$ para algún entero n. Un conjunto X es aritmético en un conjunto Y, lo que se expresa como $X\leq _{A}Y$ , si X es definible por alguna fórmula en el lenguaje de aritmética de Peano extendido por un predicado de pertenencia en Y. En forma equivalente, X es aritmético en Y si X se encuentra en $\Sigma _{n}^{0,Y}$ o $\Pi _{n}^{0,Y}$ para algún entero n. Un sinónimo de $X\leq _{A}Y$ es: X es aritméticamente reducible a Y

La relación $X\leq _{A}Y$ es reflexiva y transitiva, y por lo tanto la relación $\equiv _{A}$ definida por la regla

X\equiv _{A}Y\Leftrightarrow X\leq _{A}Y\land Y\leq _{A}X

es una relación de equivalencia. Las clases de equivalencia de esta relación son llamadas los grados aritméticos; los mismos se encuentran parcialmente ordenados en $\leq _{A}$ .

La jerarquía aritmética de los subconjuntos de espacios de Cantor y Baire[editar]

El espacio de Cantor, expresado por $2^{\omega }$ , es el conjunto de todas las infinitas sucesiones de ceros (0) y unos (1); el espacio de Baire, expresado por $\omega ^{\omega }$ or ${\mathcal {N}}$ , es el conjunto de todas las infinitas sucesiones de números naturales. Notar que elementos del espacio de Cantor pueden ser identificados con conjuntos de enteros y elementos del espacio de Baire con funciones de enteros en enteros.

La axiomatización ordinaria de aritmética de segundo orden utiliza un lenguaje basado en conjuntos en el cual los cuantificadores de conjunto pueden ser interpretados como cuantificando sobre el espacio de Cantor. A un subconjunto del espacio de Cantor se le asigna la clasificación $\Sigma _{n}^{0}$ si es definible por una fórmula del tipo $\Sigma _{n}^{0}$ . Al conjunto se le asigna la clasificación $\Pi _{n}^{0}$ si es definible por una fórmula del tipo $\Pi _{n}^{0}$ . Si el conjunto satisface simultáneamente $\Sigma _{n}^{0}$ y $\Pi _{n}^{0}$ entonces se le da la clasificación adicional $\Delta _{n}^{0}$ . Por ejemplo sea $O\subset 2^{\omega }$ el conjunto de todas las cadenas binarias que no son todos 0 (o en forma equivalente el conjunto de todos los conjuntos de enteros no vacíos). Como $O=\{X\in 2^{\omega }|\exists n(X(n)=1)\}$ se observa que $O$ es definido por una fórmula $\Sigma _{1}^{0}$ y por lo tanto es un conjunto $\Sigma _{1}^{0}$ .

Es de destacar que si bien ambos elementos del espacio de Cantor (que son conjuntos de enteros) y subconjuntos del espacio de Cantor son clasificados en jerarquías aritméticas, estas no poseen la misma jerarquía. De hecho las relaciones entre estas dos jerarquías son interesantes y no triviales. Por ejemplo los elementos $\Pi _{n}^{0}$ del espacio de Cantor en general no son los mismos elementos $X$ del espacio de Cantor, de forma tal que $\{X\}$ es un subconjunto $\Pi _{n}^{0}$ del espacio de Cantor. Sin embargo, numerosos resultados interesantes relacionan estas dos jerarquías.

Existen dos maneras en que se puede clasificar en la jerarquía aritmética un subconjunto del espacio de Baire.

Un subconjunto del espacio de Baire tiene un subconjunto correspondiente del espacio de Cantor según el mapa que va desde cada función de $\omega$ a $\omega$ a la función característica de su grafo. A un subconjunto del espacio de Baire se le da la clasificación $\Sigma _{n}^{1}$ , $\Pi _{n}^{1}$ , o $\Delta _{n}^{1}$ si y solo si el correspondiente subconjunto del espacio de Cantor posee la misma clasificación.
Una definición equivalente de la jerarquía analítica en un espacio de Baire es si se define la jerarquía analítica de las fórmulas usando una versión funcional de aritmética de segundo orden; entonces la jerarquía analítica en subconjuntos del espacio de Cantor puede ser definida a partir de la jerarquía en el espacio de Baire. Esta definición alternativa arroja exactamente las mismas clasificaciones que la primera definición.

Una definición similar se utiliza para definir la jerarquía aritmética en potencias cartesianas finitas del espacio de Baire o espacio de Cantor, utilizando fórmulas con varias variables libres. La jerarquía aritmética puede ser definida en todo espacio polaco efectivo; la definición es particularmente simple para espacios de Cantor y de Baire porque ellos se ajustan al lenguaje de la ordinario de la aritmética de segundo orden.

Notar que también podemos definir la jerarquía aritmética de subconjuntos de espacios de Cantor y Baire en forma relativa a algunos conjuntos de enteros. De hecho ${\mathbf {\Sigma }}_{n}^{0}$ en letras negritas es la unión de $\Sigma _{n}^{0,Y}$ para todos los conjuntos de enteros Y. Notar que la jerarquía en negritas es la jerarquía estándar de los conjuntos de Borel.

Véase también[editar]

Referencias[editar]

G.Japaridze, "The logic of the arithmetical hierarchy", Annals of Pure and Applied Logic 66 (1994), pp.89-112.
Moschovakis, Yiannis N. (1980). Descriptive Set Theory. North Holland. ISBN 0-444-70199-0.
Rogers, H. (1967). Theory of recursive functions and effective computability. McGraw-Hill.

Datos: Q669094