Gnome sort

El algoritmo de ordenación conocido como gNome_sort tiene una historia de invención cuasi paralela. Durante un tiempo existió la polémica sobre su invención, finalmente atribuida a Hamid Sarbazi-Azad quien lo desarrolló en el año 2000 y al que llamó Stupid sort (Ordenamiento estúpido).

Cuando Dick Grune lo inventó (más apropiadamente, lo reinventó) y documentó,​ no halló evidencias de que existiera y en palabras suyas, dijo de él "the simplest sort algorithm"​ (es el algoritmo más simple) y quizás tenga razón, pues lo describió en sólo cuatro líneas de código. Dick Grune se basó en los gnomos de jardín holandés y la manera en que se colocan dentro de los maceteros (ver la referencia anterior) y de ahí también el nombre que le dio.

Netamente es un algoritmo de burbuja con una clara particularidad: recorre el array a ordenar como una cremallera, en un vaivén, o bien puede ser definido como un ordenamiento de burbuja bidireccional, que a su vez son llamados también cocktail shaker (agitador de cócteles), por la forma en que trabaja...

Cumple estrictamente hablando con la complejidad O(n²).

Descripción

El algoritmo empieza comparando la primera pareja de valores. Si están en orden incrementa el puntero y vuelve a realizar la comparación: si no están en orden, se pasa el menor a la izquierda y el mayor a la derecha, y se reduce el puntero. Ahora la comparación es con el elemento anterior, y si no hay un elemento anterior se pasa al siguiente elemento. Cuando el puntero alcanza el extremo superior del array, ya está totalmente ordenado.

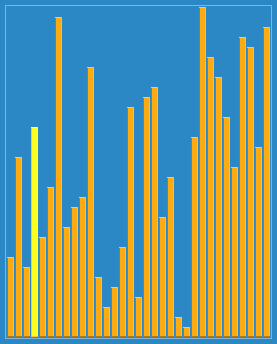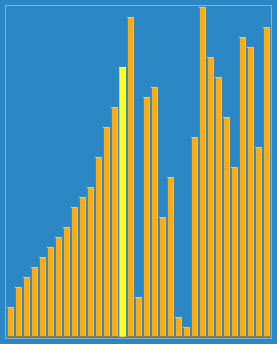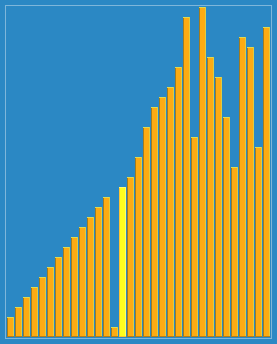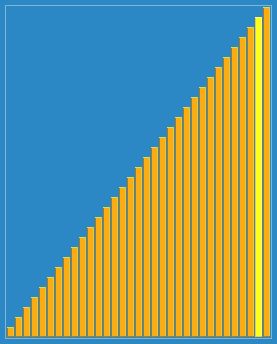
Cuando compara hacia arriba va sin hacer intercambios, es que el par bajo examen está ordenado entre sí, y cuando compara hacia abajo, va haciendo intercambios. El proceso aparece como un zigzagueo continuo a un lado y otro.

La operación empieza por el puntero en el punto más bajo y cuando llega al extremo superior ha terminado de ordenar el array.

Para realizar un ordenamiento inverso basta cambiar la decisión de intercambio de los elementos, es decir, dejar los mayores abajo y los menores arriba.

Pseudocódigo

  i ← 1
  Mientras i ≤ len- 1
    Si a[i-1] ≤ a[i]
        i ← i+1
    Sino
        temp ← a[i-1]
        a[i-1] ← a[i]
        a[i] ← temp
        i ← i-1
        Si i = 0
          i ← 1
        Finsi
    Finsi
  FinMientras

Enlaces externos

• Distintas implementaciones del algoritmo en Wikibooks (inglés)
• Distintas implementaciones del algoritmo en RosettaCode.org

• Datos: Q936797