Estructuras de Michell
Las estructuras de Michell son estructuras que son óptimas según los criterios definidos por A.G.M. Michell en su artículo de 1904, al que se hace referencia con frecuencia en la bibliografía anglosajona.[1]
Conceptos generales
[editar]Michell establece que “una estructura reticulada (también denominada "cercha" o "celosía") es óptima, es decir, alcanza el límite de economía de material posible en cualquier configuración estructural bajo las mismas fuerzas aplicadas, si el espacio ocupado por la estructura puede ser sometido a una pequeña deformación apropiada, de manera que las deformaciones en todas las barras de la retícula se incrementan en fracciones proporcionales a sus longitudes, y no menos que el cambio fraccional de longitud de cualquier elemento de la estructura”.
La conclusión anterior se basa en el teorema de la ruta de carga de Maxwell:
donde es el valor de la tracción en cualquier elemento traccionable de longitud , es el valor de la compresión en cualquier elemento comprimible de longitud y es un valor constante que se basa en las cargas externas aplicadas a la estructura.
Según el teorema de la trayectoria de carga de Maxwell, la reducción de la trayectoria de carga de los elementos sometidos a tracción reducirá en el mismo valor la trayectoria de carga de los elementos sometidos a compresión para un conjunto dado de cargas externas. La estructura con trayectoria de carga mínima es aquella que tiene un cumplimiento estructural mínimo (es decir, que tiene una deflexión ponderada mínima en los puntos de las cargas aplicadas ponderadas por los valores de estas cargas). En consecuencia, las estructuras de Michell son cerchas de cumplimiento estructural mínimo.
Casos especiales
[editar]1. Todas las barras de una celosía están sujetas a una carga del mismo signo (tracción o compresión).
El volumen de material requerido es el mismo para todos los casos posibles para un conjunto dado de cargas. Michell define el volumen mínimo requerido de material como:
donde es la tracción permitida en el material.
2. Barras de tracción y compresión mixtas
Un caso más general son las celosías que consisten en barras que tanto antes como después de la deformación apropiada, forman curvas de sistemas ortogonales. Un sistema ortogonal bidimensional permanece ortogonal después de estirar una serie de curvas y comprimir otra con igual deformación si y solo si la inclinación entre dos curvas adyacentes cualesquiera de la misma serie es constante en toda su longitud. Este requisito da como resultado que la serie perpendicular de curvas sea:
a) Sistemas de tangentes y evolventes o
b) Sistemas de intersección de espirales logarítmicas.
Debe tenerse en cuenta que la línea recta o la circunferencia son casos especiales de una espiral logarítmica.
Ejemplos
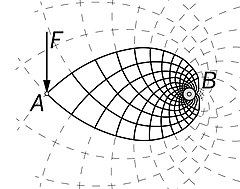
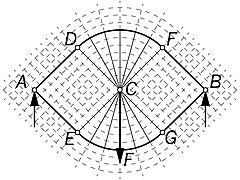
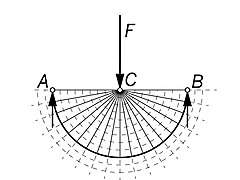
[editar]Michell proporcionó varios ejemplos de cerchas óptimas:
Celosías de Prager
[editar]
En los últimos años se han realizado muchos estudios sobre cerchas óptimas discretas.[2][3][4] A pesar de que las estructuras de Michell se definen para el continuo (número infinito de elementos), a veces también se las llama cerchas de Michell. William Prager realizó una contribución significativa al tema de las cerchas óptimas discretas, y utilizó el método del círculo de desplazamientos relativos para llegar a la topología óptima de dichas cerchas (típicamente voladizos). Para reconocer la contribución de William Prager, las cerchas Michell discretas a veces se denominan cerchas Prager. Posteriormente, la geometría de las cerchas Prager en voladizo fue formalizada por Mazurek, Baker y Tort[5][6], quienes advirtieron ciertas relaciones geométricas entre los miembros de las cerchas discretas óptimas para problemas de 3 puntos o 3 fuerzas.
Referencias
[editar]- ↑ Michell, A. G. M. (1904) The limits of economy of material in frame-structures, Philosophical Magazine, Vol. 8(47), p. 589-597.
- ↑ Prager W., A Note on Discretized Michell Structures, Computer Methods in Applied Mechanics and Engineering, Vol. 3, pp. 349-355, 1974
- ↑ Prager W. Optimal layout of cantilever trusses, Journal of Optimization Theory and Applications (1977) 23: 111. https://doi.org/10.1007/BF00932301
- ↑ Prager W. Nearly optimal design of trusses, Computers & Structures, ISSN 0045-7949, Vol: 8, Issue: 3, Page: 451-454, 1978
- ↑ Mazurek, A., Baker W.F. & Tort, C., Geometrical aspects of optimum truss like structures, Structural and Multidisciplinary Optimization (2011) 43: 231. https://doi.org/10.1007/s00158-010-0559-x
- ↑ Mazurek, A., Geometrical aspects of optimum truss like structures for three-force problem, Structural and Multidisciplinary Optimization (2012) 45: 21. https://doi.org/10.1007/s00158-011-0679-y