Semejanza (geometría)

Dos triángulos son semejantes si existe una relación de semejanza o similitud entre ambos.

Introducción

Una semejanza es la composición de una isometría (o sea, una rotación y una posible reflexión o simetría axial) con una homotecia.En la rotacion se puede cambiar el tamaño y la orientación de una figura pero no se altera su forma.

Por lo tanto, dos triángulos son semejantes si tienen similar forma.

En el caso del triángulo, la forma sólo depende de sus ángulos (no así en el caso de un rectángulo, por ejemplo, donde todos sus ángulos son rectos pero cuya forma puede ser más o menos alargada, es decir que depende del cociente base / altura).

Se puede simplificar así la definición: dos triángulos son semejantes si sus ángulos son iguales dos a dos.

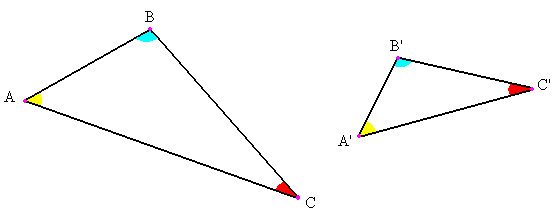
En la figura, los ángulos correspondientes son A = A', B = B' y C = C'. Para denotar que dos triángulos ABC y DEF son semejantes se escribe ABC ~ DEF, donde el orden indica la correspondencia entre los ángulos: A, B y C se corresponden con D, E y F, respectivamente.

Una similitud tiene la propiedad (que la caracteriza) de multiplicar todas la longitudes por un mismo factor. Por lo tanto las razones longitud imagen / longitud origen son todas iguales, lo que da una segunda caracterización de los triángulos semejantes:

Dos triángulos son semejantes si las razones de los lados correspondientes son congruentes.

Ecuación

Se reúnen estas dos propiedades equivalentes en la siguiente ecuación:

$(ABC\sim A'B'C')\Longleftrightarrow {\begin{Bmatrix}{\widehat {A}}={\widehat {A}}'\\{\widehat {B}}={\widehat {B}}'\\{\widehat {C}}={\widehat {C}}'\end{Bmatrix}}\Longleftrightarrow \left({\frac {\overline {A'B'}}{\overline {AB}}}={\frac {\overline {A'C'}}{\overline {AC}}}={\frac {\overline {B'C'}}{\overline {BC}}}\right)$

Corolarios

• Todos los triángulos equiláteros son semejantes.
• Si dos triángulos tienen dos ángulos iguales, los terceros también son iguales.

Propiedades de la semejanza

Propiedad reflexiva, refleja o idéntica

Todo triángulo es semejante a sí mismo.

Propiedad idéntica o simétrica

Si un triángulo es semejante a otro, aquel es semejante al primero.

Propiedad transitiva

Si un triángulo es semejante a otro, y éste a su vez es semejante a un tercero, el primero es semejante al tercero.

Teorema de Thales

Un caso particular es el que se da en el teorema de Thales, donde los triángulos tienen dos lados (vistos como rectas) comunes: (CA) = (CA') y (CB) = (CB'), y los lados restantes son dos catetos paralelos: (AB) // (A'B').

Archivo:Triángulos semejantes Thales.svg

Triángulos semejantes según el teorema de Thales

Los lados son así paralelos dos a dos y, por lo tanto, definen ángulos iguales (del mismo color en la figura). Por ello, los triángulos CAB y CA'B' son semejantes (de hecho son homotéticos), lo que implica la igualdad de los cocientes:

$({\frac {\overline {CA'}}{\overline {CA}}})=({\frac {\overline {CB'}}{\overline {CB}}})=({\frac {\overline {A'B'}}{\overline {AB}}})$

Otro teorema famoso de la geometría, el teorema de Pitágoras, es también una consecuencia inmediata de la doble caracterización de los triángulos semejantes.

Teorema fundamental de la semejanza de triángulos

Toda paralela a un lado de un triángulo que no pase por el vértice opuesto, determina con las rectas a las que pertenecen los otros dos lados, un triángulo semejante al dado.

H)

ABC; r || AC

r corta AB en L

r corta BC en M

T) $(BLM\sim BAC)$

D)

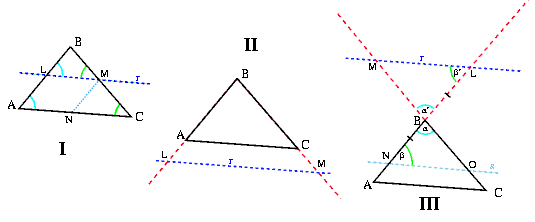
Podrán presentarse 3 casos:

I - r corta a los lados AB y BC por puntos interiores a ellos.

Haremos una primera consideración, referida a los ángulos, y la llamaremos (1):

$\wedge B=\wedge B$ por carácter reflejo

$\wedge BLM=\wedge A$ por ser correspondientes entre r || BC, secante AB

$\wedge BML=\wedge C$ por ser correspondientes entre r || BC, secante AC

Por otra parte, en virtud del corolario del Teorema de Tales se tiene:

${\frac {BL}{BA}}={\frac {BM}{BC}}\qquad \bigotimes$

Si por M se traza una paralela al lado AB, esta interseca al lado AC en un punto N, y nuevamente por el corolario del Teorema de Tales tenemos:

${\frac {BM}{BC}}={\frac {AN}{AC}}\qquad \bigoplus$

Pero dado que AN = LM, por ser lados opuestos del paralelogramo ALMN, reemplazando en $\bigoplus$ se obtiene:

${\frac {BM}{BC}}={\frac {LM}{AC}}\qquad \bigodot$

De $\bigotimes$ y $\bigodot$ se obtiene la consideración que llamaremos (2):

${\frac {BL}{BA}}={\frac {BM}{BC}}={\frac {LM}{AC}}$

Luego de (1) y (2), resulta:

$BLM\sim BAC$ por definición de semejanza.

II - r corta a las rectas de los lados AB y BC por puntos exteriores a ellos, sobre las semirrectas de origen B que los contienen.

Consideramos BLM como si fuera el triángulo dado, y BAC el triángulo nuevo, y por el caso I de la demostración, es:

$(BAC\sim BLM)\Rightarrow (BLM\sim BAC)$ por carácter simétrico.

III - r corta a las rectas de los lados AB y BC en puntos que pertenecen a las semirrectas opuestas a las que sirven de sostén a dichos lados.

Sobre la semirrecta de origen B que contiene al punto A, se construye BN=BL y por el extremo N del segmento construido, una paralela a AC (s) que corta la recta de BC por O.

Quedan entonces $BNO\sim BAC$ por el caso I, semejanza que llamaremos $\otimes$.

Teniendo en cuenta los triángulos BNO y BLM, se observa:

• BN=BM por construcción
• α=α' por ser opuestos por el vértice.
• β=β' por ser alternos internos entre r || s, secante MN

Y siendo BNO=BLM es BNO ~ BLM $\oplus$ por el primer corolario de la definición.

De $\otimes$ y $\oplus$, y por carácter transitivo:

BAC ~ BLM $\Rightarrow$ BLM ~ BAC

Geometrías no-euclídeas

La posibilidad de aumentar el tamaño de una figura sin modificar su forma es tan obvia y natural que durante milenios se pensó que era una consecuencia de los axiomas de la geometría, y se trató en vano de demostrarlo desde la Grecia antigua. Sin embargo, al estudiar otras geometrías, las no euclidianas, los matemáticos del siglo XIX, entre ellos Bernhard Riemann y Nikolái Lobachevski se dieron cuenta que esto sólo sucedía en los espacios euclídeos, es decir, sin curvatura.

Se puede definir una geometría sobre la esfera, por ejemplo: Los segmentos son los caminos más cortos que unen sus extremos y las rectas son las líneas geodésicas, a semejanza de los ecuadores de la esfera. El análogo de una homotecia se construye así: se escoge un punto O de la superficie como centro de la homotecia, y para definir la imagen de otro punto A se traza la geodésica que pasa por O y A (que es única si A no es el punto diametralmente opuesto a O), consideramos que O es el origen de esta línea y A el punto de abscisa 1. La imagen A' será el punto de abscisa k, donde k es la razón de la homotecia. En la figura se ha tomado k = 3 y se han construido las imágenes de B y C también.

Triángulos semejantes en la geometría de Riemann.

Se observa que la imagen del "triángulo" ABC es el "triángulo A'B'C', es decir que los catetos A'B', A'C' y B'C' son segmentos de líneas geodésicas, y que A'B'C' merece ser llamado triángulo semejante (por no decir homotético) al triángulo ABC.

Al aplicar la construcción precedente al pequeño triángulo ABC de la superfice de la esfera (pequeño en comparación con el diámetro), la suma de sus ángulos será ligéramente superior a π radianes (180º), pero el triángulo A'B'C' tendrá ángulos de mayor amplitud, siendo su suma mucho mayor que π radianes, como se ve en la figura. El aumento de tamaño implica aquí claramente un cambio de forma.

En conclusión, los triángulos semejantes permiten saber en que clase de espacio nos hallamos, uno euclidiano, o con curvatura positiva (como la esfera), o con curvatura negativa (espacio hiperbólico), y la doble caracterización de los triángulos similares (mismos ángulos y cocientes de los lados iguales) en la geometría usual no es ni anecdótico ni anodino.