Terna pitagórica

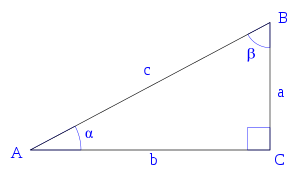
Una terna pitagórica consiste en tres enteros positivos a, b, c que cumplen que a² + b² = c². El nombre deriva del teorema de Pitágoras, el cual plantea que cualquier triángulo rectángulo con una longitud entera de sus lados forma una terna pitagórica. Lo inverso también es verdadero, cualquier terna pitagórica forma un triángulo rectángulo.

Por ejemplo:

a	b	c
3	4	5
5	12	13
6	8	10
7	24	25
8	15	17
9	12	15
9	40	41

Si (a, b, c) es una terna pitagórica, también lo es (da, db, dc) para cualquier número entero positivo d. Una terna pitagórica primitiva es aquella en la que el máximo común divisor de a, b y c es 1. Si (a, b, c) es una terna pitagórica primitiva, entonces el número d es el máximo común divisor de los tres números da, db, dc. Los triángulos que se hacen con una terna pitagórica no primitiva son siempre proporcionales a otro triángulo cuyos lados forman una terna pitagórica primitiva.

Si m > n son enteros positivos, entonces:

a = m² − n²,

b = 2mn,

c = m² + n²

es una terna pitagórica. Es primitiva si y sólo si m y n son coprimos y solamente uno de ellos es par (si ambos n y m son impares, entonces a, b y c serán pares, y la terna no será una terna pitagórica primitiva). No todas las ternas pitagóricas pueden ser generadas con las expresiones anteriores, pero todas las ternas primitivas surgen de este modo de un único par de números coprimos m > n. Así pues, existe un número infinito de ternas pitagóricas primitivas.

Si representamos en un plano los puntos que cumplen las condiciones para ser una terna pitagórica, obtenemos el siguiente patrón de puntos (ver imagen de la derecha). Los puntos rojos representan las ternas primitivas y los puntos azules aquellas ternas que no lo son. Como se observa la imagen tiene un eje de simetría debido a que es posible intercambiar a por b y viceversa y obtendremos de nuevo otra terna pitagórica.

Es interesante hacer notar que existe más de una terna primitiva con el mismo número entero menor. El primer ejemplo de esto es el 20, el cual es el menor entero de dos ternas primitivas: 20 21 29 y 20 99 101

En contraste el número 1229779565176982820 es el menor entero de 15386 ternas primitivas, la menor y mayor de ellas del que forma parte son:

1229779565176982820
1230126649417435981
1739416382736996181

y

1229779565176982820
378089444731722233953867379643788099
378089444731722233953867379643788101.

Por curiosidad, consideremos la factorización en números primos:

1229779565176982820 = 2² × 3 × 5 × 7 × 11 × 13 × 17 × 19 × 23 × 29 × 31 × 37 × 41 × 43 × 47.

También se puede considerar la siguiente, que señala que la diferencia entre la hipotenusa y el cateto par es siempre un número impar al cuadrado; y con el cateto impar, el doble de otro número al cuadrado.

Para todo p, q números naturales

a= 2pq +q²

b= 2pq + 2p²

c= 2pq + 2p² + q²

Se observa que si p=q se obtiene la terna más conocida (3,4,5) o cualquiera de sus derivadas.

Aquí tenemos la formula original de los pitagóricos para generar ternas primitivas:

Para cualquier par de números enteros positivos " y > x " impares y coprimos,

donde el producto " xy = i " es el cateto impar y "(y² － x²) / 2 = p " es el cateto par,

siendo "(y² + x²) / 2 = h" la hipotenusa y el radio del incentro "r = x(y － x) / 2",

teniendo además que "y( x + y )" ó "y² + ( x y )" es igual al perímetro del triángulo

y si sabemos que el perímetro por el radio del incentro es el duplo de su área,

podemos deducir que " x y ( x + y ) ( y - x ) / 2² " sera igual a el Área de la triada,

recordando que " h － p = x² " es fácil obtener " h + p = y² " de cualquier terna primitiva.

Para n y m coprimos "m - n = x" y "n + m = y" ó "(y － x) / 2 = n" y "( x + y ) / 2 = m"

donde "n ( m - n ) = r " y "( m - n ) ( n + m ) n m = A" para " A / ( r / 2 ) " igual al perímetro.

Relación entre todas las ternas

Si consideramos (x,y,z) como una terna pitagórica, podemos establecer la siguiente relación:

r=x+y-z

a=x-r

b=y-r

De la ecuación (a+b+r)² = (r+a)² + (r+b)² se puede deducir que r² = 2ab

En este punto podemos plantear igualmente

s=a+b-r

j=a-s

k=b-s

y sustituyendo en r² = 2ab obtenemos:

(j+k+s)² = 2(j+s)(k+s)

s² = j² + k²

De donde se deduce que todas las ternas pitagóricas están relacionadas entre sí.

La fórmula resultante es la siguiente:

Para toda terna que cumpla s² = j² + k², se pueden hallar hasta otras 8 ternas (8, pues la solución es posible con números positivos y negativos) del tipo (x,y,z) tal que:

x = ±2k ±2s ±j

y = ±2j ±2s ±k

z= ±2s ±2(j+k) ±s

Resultando que todas las posibles soluciones están relacionadas entre sí en forma de árbol, tal como muestra la figura (dónde sólo se muestran las ternas con números naturales o enteros positivos). En amarillo, las ternas llamadas "cojas", donde la diferencia entre uno de los lados es 1 o 2.

(...)

Implementación en lenguajes de programación

Haskell

El siguiente código genera la lista de las x ternas pitagóricas

{-
	Función para determinar las n primeras ternas pitagóricas
-}

terPit :: Integer -> [[Integer]]
terPit x = [[a,b,c] | m <- [2..x],n <- [1..x] ,a <- [m^2-n^2], b <- [2*m*n], c <- [n^2+m^2], m > n]

Pitágoras y Fermat

El último teorema de Fermat plantea que no existen ternas no triviales análogas a las ternas pitagóricas para exponentes mayores que dos con números naturales. Sin demostración durante más de 300 años, Andrew Willes consiguió una demostración en 1994 que imposibilita la ecuación. Por lo tanto quedo así:

La ecuación: $z^{n}=x^{n}+y^{n}$ no tiene solución si n>2 con x, y, z naturales.

Enlaces externos

• http://mathworld.wolfram.com/PythagoreanTriple.html plantea una extensa discusión sobre las ternas pitagóricas (en inglés).
• http://www.math.clemson.edu/~rsimms/neat/math/pyth/ posee una calculadora Javascript con las fórmulas (m² − n², 2mn, m² + n²) y como se llegan a ellas (en inglés).
• http://www.monografias.com/trabajos5/numelem/numelem.shtml?monosearch