Ecuación de van Deemter

La ecuación de Van Deemter en cromatografía relaciona la variación por unidad de longitud de una columna de separación con la velocidad de fase móvil lineal considerando las propiedades físicas, cinéticas y termodinámicas de una separación.^[1] Estas propiedades incluyen vías dentro de la columna, difusión (axial y longitudinal) y cinética de transferencia de masa entre fases estacionarias y móviles. En la cromatografía de líquidos, la velocidad de la fase móvil se toma como la velocidad de salida, es decir, la relación del caudal en ml / segundo al área de la sección transversal de la "trayectoria de flujo de salida de columna". Para una columna empaquetada, el área de la sección transversal de la trayectoria de flujo de salida de la columna generalmente se toma como 0,6 veces el área de la sección transversal de la columna. Alternativamente, la velocidad lineal puede tomarse como la relación de la longitud de la columna al tiempo muerto. Si la fase móvil es un gas, entonces se debe aplicar la corrección de presión. La variación por unidad de longitud de la columna se toma como la relación entre la longitud de la columna y la eficiencia de la columna en placas teóricas . La ecuación de Van Deemter es una función hiperbólica que predice que hay una velocidad óptima a la que habrá la varianza mínima por unidad de longitud de la columna y, por lo tanto, una eficiencia máxima. La ecuación de Van Deemter fue el resultado de la primera aplicación de la teoría de la velocidad al proceso de elución de la cromatografía.

Ecuación de van Deemter

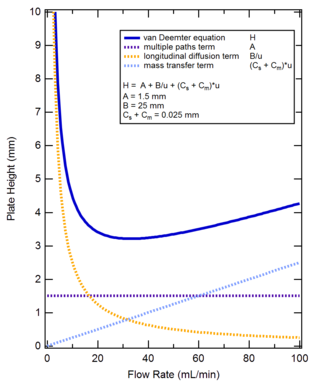
La ecuación de van Deemter relaciona la altura equivalente a una placa teórica (HETP) de una columna cromatográfica con los diversos parámetros de flujo y cinéticos que causan la ampliación del pico, como sigue:

HETP=A+{\frac {B}{u}}+(C_{s}+C_{m})\cdot u

Donde

HETP = una medida del poder de resolución de la columna [m]
A = parámetro de difusión turbulenta, relacionado con la canalización a través de un embalaje no ideal [m]
B = coeficiente de difusión de las partículas que eluyen en la dirección longitudinal, lo que resulta en la dispersión [m² s^-1 ]
C = Resistencia al coeficiente de transferencia de masa del analito entre la fase móvil y la estacionaria [s]
u = Velocidad lineal [ms⁻¹]

En capilares tubulares abiertos, el término A será cero, ya que la falta de empaquetamiento significa que no se produce canalización. Sin embargo, en las columnas empaquetadas, existen múltiples rutas distintas ("canales") a través del empaquetamiento de la columna, lo que resulta en la expansión de la banda. En este último caso, A no será cero.

La forma de la ecuación de van Deemter es tal que HETP alcanza un valor mínimo a una velocidad de flujo particular. A este caudal, el poder de resolución de la columna se maximiza, aunque en la práctica, es probable que el tiempo de elución no sea práctico. Al diferenciar la ecuación de van Deemter con respecto a la velocidad, al establecer la expresión resultante en cero y al resolver la velocidad óptima se obtiene lo siguiente:

u={\sqrt {\frac {B}{C}}}

Recuento de placas

H={\frac {L}{N}}\,

con $L\,$ la longitud de la columna y $N\,$ el número de placas teóricas se puede estimar a partir de un cromatograma mediante el análisis del tiempo de retención $t_{R}\,$ para cada componente y su desviación estándar $\sigma \,$ como medida del ancho de pico, siempre que la curva de elución represente una curva gaussiana .

En este caso, el recuento de placas viene dado por:^[2]

N=\left({\frac {t_{R}}{\sigma }}\right)^{2}\,

Usando el ancho de pico más práctico a media altura $W_{1/2}\,$ la ecuación es:

N=8\ln(2)\cdot \left({\frac {t_{R}}{W_{1/2}}}\right)^{2}\,

o con el ancho en la base del pico:

N=16\cdot \left({\frac {t_{R}}{W_{base}}}\right)^{2}\,

Van Deemter ampliada

La ecuación de Van Deemter se puede ampliar aún más a:^[3]

H=2\lambda d_{p}+{2\gamma D_{m} \over u}+{\omega (d_{p}{\mbox{ or }}d_{c})^{2}u \over D_{m}}+{Rd_{f}^{2}u \over D_{s}}

Donde:

H es la altura de la placa
λ es la forma de partícula (con respecto al embalaje)
d _p es el diámetro de partícula
γ, ω y R son constantes
D _m es el coeficiente de difusión de la fase móvil.
d _c es el diámetro capilar
d _f es el espesor de la película
D _s es el coeficiente de difusión de la fase estacionaria.
u es la velocidad lineal

Véase también

Referencias

↑ van Deemter JJ, Zuiderweg FJ and Klinkenberg A (1956). «Longitudinal diffusion and resistance to mass transfer as causes of non ideality in chromatography». Chem. Eng. Sci. 5: 271-289. doi:10.1016/0009-2509(56)80003-1.
↑ Unión Internacional de Química Pura y Aplicada. «plate number, N». Compendium of Chemical Terminology. Versión en línea (en inglés).
↑ Kazakevich, Yuri. «Band broadening theory (Van Deemter equation)». Seton Hall University. Archivado desde el original el 8 de enero de 2014. Consultado el 5 de febrero de 2014.

Datos: Q900511

[1] van Deemter JJ, Zuiderweg FJ and Klinkenberg A (1956). «Longitudinal diffusion and resistance to mass transfer as causes of non ideality in chromatography». Chem. Eng. Sci. 5: 271-289. doi:10.1016/0009-2509(56)80003-1.

[2] Unión Internacional de Química Pura y Aplicada. «plate number, N». Compendium of Chemical Terminology. Versión en línea (en inglés).

[3] Kazakevich, Yuri. «Band broadening theory (Van Deemter equation)». Seton Hall University. Archivado desde el original el 8 de enero de 2014. Consultado el 5 de febrero de 2014.

[1]

[2]

[3]