Slope One

El filtrado colaborativo es una técnica usada por los Sistemas de Recomendación para combinar las opiniones y pruebas de diferentes usuarios con el fin de obtener recomendaciones personalizadas. Hay al menos dos clases de filtrados colaborativos: las técnicas basadas en usuarios son derivadas de la medición de similitudes entre usuarios, mientras que las técnicas basadas en artículos comparan las valoraciones dadas por distintos usuarios. Slope One es una familia de algoritmos usados para el Filtrado Colaborativo introducida en Slope One Predictors for Online Rating-Based Collaborative Filtering por Daniel Lemire y Anna Maclachlan. Posiblemente, esta es la forma más simple de filtrado colaborativo basado en artículos. Su simplicidad la hace especialmente sencilla de implementar eficientemente mientras que su exactitud está a la par de algoritmos más complejos y costosos.

Filtrado colaborativo basado en artículos de recursos valorados y overfitting[editar]

Cuando la valoración de los artículos está disponible, como es el caso cuando las personas tienen la opción de ofrecer su valoración (entre 1 y 5, por ejemplo), el filtrado colaborativo ayuda a predecir la valoración de un individuo basado en su historial de valoraciones y en una (gran) base de datos de valoraciones conformada por otros usuarios.

Ejemplo. ¿Podemos predecir la valoración que un individuo pudiera dar al nuevo álbum de Celine Dion teniendo que le otorgó 5 de 5 a Los Beatles?

En este contexto, un Filtrado Colaborativo basado en artículos^[1]^[2] predice las valoraciones de un artículo basado en las valoraciones de otro, típicamente usando regresión lineal ( $f(x)=ax+b$ ). Por lo tanto, si tenemos 1000 artículos, pudiera haber hasta 1.000.000 de regresiones lineales por aprender, y entonces, hasta 2.000.000 de regresores. Este enfoque puede sufrir de overfitting^[3] a menos que se seleccionen solamente los pares de elementos para los cuales varios usuarios hayan valorado ambos artículos.

Una mejor alternativa puede ser aprender un predictor simple como $f(x)=x+b$ : los experimentos demuestran que este predictor simple (llamado Slope One) algunas veces supera^[3] la regresión lineal mientras que tiene la mitad del número de regresores. Este enfoque simplificado también reduce los requerimientos de almacenamiento y la latencia.

El filtrado colaborativo basado en artículos es solo una forma más de filtrado colaborativo. Otras alternativas incluyen el filtrado colaborativo basado en usuarios donde las relaciones entre los usuarios son de intereses. En cualquiera de los casos, el filtrado colaborativo basado en artículos es especialmente escalable con respecto al número de usuarios.

Filtrado colaborativo basado en artículos de estadísticas de compra[editar]

No siempre se otorgan valoraciones: cuando los usuarios solo proveen datos sobre si se compró o no el artículo, entonces Slope One y otros algoritmos basados en valoraciones no aplican. Ejemplos de algoritmos binarios sobre filtrado colaborativo basado en artículos incluyen al Algoritmo artículo-a-artículo patentado de Amazon^[4] el cual calcula el coseno entre vectores binarios que representan las compras en una matriz usuario-artículo.

Siendo posiblemente más simple que incluso Slope One, el algoritmo de artículo-a-artículo ofrece un interesante punto de referencia. Permítanos mostrarle un ejemplo.

Estadísticas de compra
Cliente	Artículo 1	Artículo 2	Artículo 3
Juan	Lo compró	No lo ha comprado	Lo compró
Marcos	No lo ha comprado	Lo compró	Lo compró
Lucía	No lo ha comprado	Lo compró	No lo ha comprado

En este caso, el coseno entre el elemento 1 y el 2 es

${\frac {(1,0,0)\cdot (0,1,1)}{\Vert (1,0,0)\Vert \Vert (0,1,1)\Vert }}=0$ ,

el coseno entre el elemento 1 y 3 es

${\frac {(1,0,0)\cdot (1,1,0)}{\Vert (1,0,0)\Vert \Vert (1,1,0)\Vert }}={\frac {1}{\sqrt {2}}}$ ,

mientras que el coseno entre el elemento 2 y el 3 es

${\frac {(0,1,1)\cdot (1,1,0)}{\Vert (0,1,1)\Vert \Vert (1,1,0)\Vert }}={\frac {1}{2}}$ .

Por lo tanto, un usuario que visite el artículo 1 recibiría como recomendación el ítem 3, un usuario que visite el ítem 2 recibiría como recomendación el ítem 3 igualmente; y finalmente, un usuario que visite el ítem 3 recibiría como recomendación el ítem 1 (y después el ítem 2). El modelo usa un solo parámetro por cada par de elementos (el coseno) para hacer la recomendación. Por lo tanto, si hay n elementos, hasta n(n-1)/2 cosenos necesitan ser calculados y almacenados.

El filtrado colaborativo para recursos valorados de Slope One[editar]

Para reducir drásticamente el sobreajuste (overfitting), mejorar el rendimiento y facilitar la implementación, fue propuesta la familia de algoritmos Slope One para el Filtrado Colaborativo basado en valoraciones para artículos. Esencialmente, en vez de usar una regresión lineal de las valoraciones de un elemento para las valoraciones de otro ( $f(x)=ax+b$ ), se usa una forma simple de regresión con un solo parámetro ( $f(x)=x+b$ ). El parámetro indicado es entonces una diferencia de promedio entre la valoración de dos elementos. Esto ha demostrado ser mucho más exacto que la regresión lineal en algunas instancias,^[3] y toma la mitad del espacio de almacenamiento o menos.

Ejemplo:

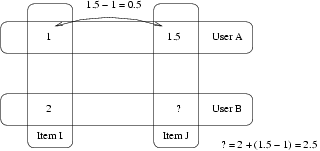
Juan dio 1 a María y 1.5 a Pedro
Carlos dio 2 a María
¿Cómo piensas que Carlos valorará a Pedro?
La respuesta de Slope One será 2.5 (1.5-1+2=2.5).

Para un ejemplo más realista, considere la siguiente tabla.

Base de datos de valoración
Cliente	Artículo 1	Artículo 2	Artículo 3
Juan	5	3	2
Marcos	3	4	Didn't rate it
Lucía	No ha valorado	2	5

En este caso, el promedio de las diferencias en las valoraciones entre el artículo 2 y el 1 es (2+(-1))/2=0.5. Entonces, en promedio, el artículo 1 es valorado antes que el 2 por 0.5. De la misma manera, el promedio de las diferencias entre el artículo 3 y el 1 es 3. Por lo tanto, si intentamos predecir la valoración de Lucía para el artículo 1 usando su valoración para el artículo 2, obtenemos 2+0.5=2.5. Asimismo, si tratamos de predecir su valoración para el artículo 1 usando la del artículo 3 obtenemos 5+3=8.

Si un usuario ha valorado varios items, las predicciones son combinadas usando un promedio ponderado donde una buena elección para esta ponderación es el número de usuario que han valorado dos items. En el ejemplo anterior, pudiéramos predecir la siguiente valoración de Lucía para el artículo 1

${\frac {2\times 2.5+1\times 8}{2+1}}={\frac {13}{3}}=4.33$

Por lo tanto, teniendo n artículos, para implementar Slope One, todo lo que se necesita es calcular y almacenar una media ponderada, en función de las veces que este valorado el artículo, de las diferencias y el número de valoraciones comunes para cada uno de los n² pares de elementos.

Complejidad algorítmica de Slope One[editar]

Suponiendo que hay n elementos, m usuarios y N valoraciones. Calculando las diferencias de valoración promedio para cada par de elementos requiere hasta n(n-1)/2 unidades de almacenamiento, y hasta m n ² unidades de tiempo. Esta cota calculada puede ser pesimista: si asumimos que los usuarios han valorado hasta y elementos, entonces es posible calcular las diferencias en no más que n²+my². Si un usuario ha ingresado x valoraciones, prediciendo una valoración simple requerirá x unidades de tiempo, y prediciendo todas las valoraciones que faltan requerirá hasta (n-x)x unidades de tiempo. Actualizando la base de datos cuando un usuario ha ingresado x valoraciones, e ingresa una nueva, requerirá x unidades de tiempo.

Es posible reducir los requerimientos de almacenamiento particionando los datos (Partición (Base de datos)) o usando almacenamiento disperso: pares de elementos que no tengan (o tengan pocos) usuarios que los hayan valorado puede ser omitidos

Sistemas de recomendación que usan Slope One[editar]

hitflip un sistema de recomendación de DVD
How Happy Un sitio de propósito general
inDiscover un sistema de recomendación de MP3
RACOFI Composer un sistema genérico de recomendación realizado por el National Research Council
Value Investing News un sitio de noticias del mercado de valores
Que libro me recomiendas sistema de recomendación de libros en español
Sopa de libros Red social de lectura en español

Software de código abierto que implementa Slope One[editar]

Python:

Una implementación en Python muy bien documentada, junto con un tutorial

Java (lenguaje de programación):

Taste: Una librería colaborativa basada en Java con soporte para Enterprise Java Beans (code sample)
Una Clase de Java implementando Slope One.
La Cofi: La librería de filtrado colaborativo basada en Java soporta algoritmos Slope One (la documentación está incompleta)

PHP:

La Librería Vogoo soporta algoritmos Slope One (PHP)
ElAPI Aspedia ECM soporta algoritmos Slope One (PHP)
Aquí se encuentra código fuente en PHP junto con un reporte técnico^[5] en algoritmos Slope One
Un módulo para Drupal CMS que implementa Slope One.
El OpenSlopeOne soporta algoritmos Slope One, es extremadamente rápido y usa únicamente PHP y MySQL

Erlang:

Philip Robinson implementó Slope One en Erlang.

Scala:

Steve Jenson implementó Slope One en Scala.

Haskell:

Bryan O'Sullivan implementó Slope One en Haskell.

Visual Basic para aplicaciones:

Una hoja de cálculo Microsoft Excel implementación de Slope One (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última). usando VBA (requiere activación de macros).

C Sharp:

Kuber implemented Weighted Slope One in C#.

T-SQL:

Charlie Zhu implemented Weighted Slope One in T-SQL.

Referencias[editar]

↑ Slobodan Vucetic, Zoran Obradovic: Collaborative Filtering Using a Regression-Based Approach. Knowl. Inf. Syst. 7(1): 1-22 (2005)
↑ Badrul M. Sarwar, George Karypis, Joseph A. Konstan, John Riedl: Item-based collaborative filtering recommendation algorithms. WWW 2001: 285-295
↑ ^a ^b ^c Daniel Lemire, Anna Maclachlan, Slope One Predictors for Online Rating-Based Collaborative Filtering, In SIAM Data Mining (SDM'05), Newport Beach, California, April 21-23, 2005.
↑ Greg Linden, Brent Smith, Jeremy York, "Amazon.com Recommendations: Item-to-Item Collaborative Filtering," IEEE Internet Computing, vol. 07, no. 1, pp. 76-80, Jan/Feb, 2003
↑ Daniel Lemire, Sean McGrath, "Implementing a Rating-Based Item-to-Item Recommender System in PHP/SQL Archivado el 11 de febrero de 2010 en Wayback Machine.", Technical Report D-01, January 2005.

Datos: Q1074337

[1] Slobodan Vucetic, Zoran Obradovic: Collaborative Filtering Using a Regression-Based Approach. Knowl. Inf. Syst. 7(1): 1-22 (2005)

[2] Badrul M. Sarwar, George Karypis, Joseph A. Konstan, John Riedl: Item-based collaborative filtering recommendation algorithms. WWW 2001: 285-295

[lemire2005-3] Daniel Lemire, Anna Maclachlan, Slope One Predictors for Online Rating-Based Collaborative Filtering, In SIAM Data Mining (SDM'05), Newport Beach, California, April 21-23, 2005.

[4] Greg Linden, Brent Smith, Jeremy York, "Amazon.com Recommendations: Item-to-Item Collaborative Filtering," IEEE Internet Computing, vol. 07, no. 1, pp. 76-80, Jan/Feb, 2003

[5] Daniel Lemire, Sean McGrath, "Implementing a Rating-Based Item-to-Item Recommender System in PHP/SQL Archivado el 11 de febrero de 2010 en Wayback Machine.", Technical Report D-01, January 2005.

[1]

[2]

[3]

[4]

[5]