Problema del conjunto de cobertura
El problema del Set Covering, también conocido por sus siglas SCP es un problema clásico en combinatoria, ciencias de la computación y teoría de la complejidad computacional. Es un problema que ha llevado al desarrollo de técnicas fundamentales para el campo de los algoritmos de aproximación.[1] También es uno de los problemas de la Lista de 21 problemas NP-completos de Karp cuya NP-completitud fue demostrada en 1972.
Dado un conjunto de elementos (llamado universo) y conjuntos cuya unión comprende el universo, el problema del conjunto de cobertura consiste en identificar el menor número de conjuntos cuya unión aun contiene todos los elementos del universo. Por ejemplo, sea y los conjuntos . Claramente, la unión de todos los conjuntos de contiene todos los elementos de . Sin embargo, podemos cubrir todos los elementos con el siguiente conjunto de elementos, con menor número de elementos: .
Definición formal[editar]
Formalmente, se puede definir un problema de cobertura de conjuntos de la siguiente forma: Sea el universo y la familia de subconjuntos de , una cobertura es una subfamilia de conjuntos cuya unión es .
Problema de decisión de cobertura de conjuntos[editar]
En el problema de decisión de cobertura de conjuntos, la entrada es un par y un entero y la pregunta es si existe un conjunto de cobertura de tamaño o menos.
Esta versión es un problema NP-completo.
Problema de optimización de cobertura de conjuntos[editar]
En el problema de optimización de cobertura de conjuntos, la entrada es un par y la tarea es encontrar un conjunto de cobertura que use los menos conjuntos posibles.
Esta versión es un problema NP-hard.
Formulación con programación lineal entera[editar]
El problema de cobertura de conjuntos se puede formular como la siguiente programación lineal de enteros (ILP por su nombre en inglés).[2]
| minimizar | (minimizar el coste total) | ||
| cumpliendo | para todo | (cubriendo todos los elementos del universo) | |
| para todo . | (todo conjunto, esté o no en conjunto de cobertura) |
Esta ILP pertenece a la clase más general de ILPs para problemas de cobertura. La diferencia de integralidad de esta ILP es, como máximo, , por lo tanto su relajación ofrece un algoritmo de aproximación de factor para el problema de cobertura mínima de conjuntos (donde es el tamaño del universo).[3]
Algoritmo voraz[editar]
El algoritmo voraz para cobertura de conjuntos elige conjuntos de acuerdo a una regla: en cada paso, elegir el conjunto que tiene el mayor número de elementos no elegidos. Se puede demostrar que este algoritmo consigue un ratio de aproximación de ,[4] donde es el tamaño del conjunto a cubrir y es el -esimo número armónico:
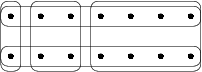
Hay un ejemplo estándar donde el algoritmo voraz obtiene un ratio de aproximación de . El universo consta de elementos. El sistema de conjuntos consiste en pares de conjuntos disjuntos con tamaños respectivamente, así como dos conjuntos disjuntos adicionales , cada uno de los cuales contiene la mitad de los elementos de cada . Con estas entradas, el algoritmo voraz coge los conjuntos , en ese orden, mientras que la solución óptima consistiría en escoger solamente y .
Un ejemplo de estas entradas para se puede observar en la figura de la derecha.
Estos resultados tan poco cercanos a la solución óptima muestran que el algoritmo voraz es esencialmente el mejor algoritmo de aproximación en tiempo polinómico para el problema de cobertura de conjuntos, entre supuestos de complejidad plausible.
Sistemas de baja frecuencia[editar]
Si cada elemento se encuentra en conjuntos como máximo, se puede encontrar una solución en tiempo polinómico que se aproxime al óptimo con dentro de un factor f usando relajación de programación lineal.[5]
Resultados poco óptimos[editar]
Lund y Yannakakis (1994) demostraron que el problema de cobertura de conjuntos no puede aproximarse en tiempo polinómico dentro de un factor de , a menos que NP tenga algoritmos de tiempo cuasi-polinómico. Feige (1998) mejoró este límite a bajo las mismas condiciones, que prácticamente coincide con el ratio de aproximación del algoritmo voraz.Raz y Safra (1997) estableció la frontera inferior de , donde es una constante, asumiendo que PNP.[6] Un resultado similar, pero con mayor valor de fue recientemente probado por Alon, Moshkovitz y Safra (2006).
Ejemplo[editar]

Una estación de bomberos tiene la capacidad de cubrir las emergencias tanto de su comuna como de las comunas adyacentes a ella, por ejemplo una estación construida en la comuna 1 (Figura 1) podrá cubrir las emergencias de todo su vecindario, es decir, de la comuna 1, comuna 2, comuna 3 y comuna 5. Se necesitan construir tantas estaciones de bomberos como sea necesario para cubrir todas las comunas ante posibles emergencias, cuidando que todas las comunas estén cubiertas por al menos una estación (una o más), minimizando el número de estaciones construidas.
Modelo matemático[editar]
Sea:
podemos formular el problema de la siguiente forma:
cumpliendo las siguientes restricciones:

Solución[editar]
Una solución para este problema sería construir estaciones en las comunas 5 y 8. Con un total de 2 estaciones construidas se lograría cubrir las necesidades de todas las comunas del problema.
Véase también[editar]
Referencias[editar]
- ↑ Vazirani (2001, p. 15)
- ↑ Vazirani (2001, p. 108)
- ↑ Vazirani (2001, pp. 110–112)
- ↑ Chvatal, V. A Greedy Heuristic for the Set-Covering Problem. Mathematics of Operations Research Vol. 4, No. 3 (Aug., 1979), pp. 233-235
- ↑ Vazirani (2001, pp. 118-119)
- ↑ Relación entre N y NP
- Alon, Noga; Moshkovitz, Dana; Safra, Shmuel (2006), «Algorithmic construction of sets for k-restrictions», ACM Trans. Algorithms (ACM) 2 (2): 153-177, ISSN 1549-6325, doi:10.1145/1150334.1150336..
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), Introduction to Algorithms, Cambridge, Mass.: MIT Press and McGraw-Hill, pp. 1033-1038, ISBN 0-262-03293-7.
- Feige, Uriel (1998), «A threshold of ln n for approximating set cover», Journal of the ACM (ACM) 45 (4): 634-652, ISSN 0004-5411, doi:10.1145/285055.285059..
- Lund, Carsten; Yannakakis, Mihalis (1994), «On the hardness of approximating minimization problems», Journal of the ACM (ACM) 41 (5): 960-981, ISSN 0004-5411, doi:10.1145/185675.306789..
- Raz, Ran; Safra, Shmuel (1997), «A sub-constant error-probability low-degree test, and a sub-constant error-probability PCP characterization of NP», STOC '97: Proceedings of the twenty-ninth annual ACM symposium on Theory of computing, ACM, pp. 475-484, ISBN 978-0-89791-888-6..
- Vazirani, Vijay V. (2001), Approximation Algorithms, Springer-Verlag, ISBN 3-540-65367-8.