Paradoja de la moneda que gira

De Wikipedia, la enciclopedia libre
La paradoja de la moneda que gira. Aunque la moneda en movimiento ha hecho una rotación completa (se pone de cabeza y regresa a su configuración inicial), solo se ha movido la mitad de la circunferencia de la moneda estacionaria.
El camino que sigue un solo punto en el borde de la moneda que gira es un cardioide.
Este artículo o sección necesita referencias que aparezcan en una publicación acreditada.
Busca fuentes: «Paradoja de la moneda que gira» – noticias · libros · académico · imágenes
Este aviso fue puesto el 2 de enero de 2018.

La paradoja de la moneda que gira es la observación no-intuitiva de que, cuando una moneda gira alrededor de la orilla de otra moneda de igual tamaño, la moneda que gira completa una rotación entera después de moverse por la mitad de la moneda estacionaria.[1]​

Descripción[editar]

El problema comienza con dos monedas idénticas. Una de ellas se hace girar alrededor de la otra, sin "resbalarse", de forma que termina del lado opuesto de donde comenzó. La moneda que gira ha hecho una rotación completa, pero solo se ha desplazado por una distancia igual a la mitad de su circunferencia.

Esto se puede visualizar colocando sobre una mesa dos monedas que se tocan en un punto. Se acomodan de tal forma que ambas tengan el mismo lado o cara hacia arriba y en paralelo. Ahora, manteniendo una moneda sin moverse, se hace girar la otra de tal forma que siempre haya un punto de contacto. Se continúa girando hasta alcanzar el lado opuesto. Ahora las monedas estarán de nuevo paralelas entre sí, desafiando la noción intuitiva.

Solución[editar]

La moneda que gira de hecho participa en dos movimientos separados, parecido a cómo se mueve la luna con respecto a la tierra (excepto que la luna completa una rotación sobre su propio eje cada vez que completa una revolución alrededor del centro de la tierra):

  • gira alrededor de su propio centro, y
  • gira alrededor del centro de la otra moneda.

El punto de contacto tanto en la moneda estacionaria como en la moneda que gira se debe mover la misma distancia, que es la mitad de la circunferencia de la moneda. Por ejemplo, el punto de contacto se mueve del lado derecho de la moneda a su lado izquierdo. De forma correspondiente, el punto de contacto en la moneda que gira debe moverse de su lado izquierdo al lado derecho. Esto quiere decir que la moneda que gira ha hecho una rotación completa alrededor de su propio centro mientras que su centro ha hecho media rotación alrededor de la moneda estacionaria.

Otra forma intuitiva de entender este problema sería imaginar qué pasa cuando un bloque o cuadrado se mueve alrededor de un círculo sin que él mismo gire. Se puede ver que el bloque hace una rotación debido a su vuelta alrededor del círculo. De esta forma, se ve que moverse alrededor del círculo añade una rotación extra, sin importar el tamaño de los círculos o monedas.

Un cuadrado que se desliza sobre un círculo, sin rotación

Radios desiguales y otras formas[editar]

Ejemplo donde R = 3r. En la figura 1, con R enderezada, el número de rotaciones (número de veces que la flecha apunta hacia arriba) es R/r = 3. En la figura 2, como R se ha restaurado en un círculo, la moneda hace una rotación extra, dando R/r + 1 = 4. (Animación)
Rotación de una moneda pequeña alrededor de otra mayor

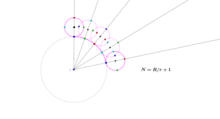
Una moneda de radio r rodando alrededor de otra de radio R hace R/r + 1 rotaciones.[2]​ Esto se debe a que el centro de la moneda rodante recorre una trayectoria circular con un radio (o circunferencia) de R + r/r = R/r + 1 veces su propio radio (o circunferencia). En el caso límite cuando R = 0, la moneda con radio r hace 0/r} + 1 = 1 rotación simple alrededor de su punto inferior.

El SAT del 1 de mayo de 1982 tenía una pregunta relativa a este problema y, debido a un error humano, tuvo que ser corregida después de que tres estudiantes demostraran que no había ninguna respuesta correcta entre las opciones.[3]​

La forma alrededor de la cual se hace rodar la moneda no necesita ser un círculo: se añade una rotación extra a la relación de sus perímetros cuando se trata de cualquier polígono simple o curva cerrada que no se interseque consigo misma. Si la forma es complejo, el número de rotaciones añadidas (o restadas, si la moneda rueda dentro de la curva) es el valor absoluto de su número de vueltas.

Otra Solución[editar]

Es una solución óptica demostrable: tenemos dos monedas de igual tamaño, la moneda A está fija o estática sobre un plano mientras que la moneda B inicialmente ubicada encima de la moneda A de tal forma que, si se traza una línea horizontal L1 sobre el plano y tomar una línea perpendicular Pr a esta, el centro de ambas monedas quede sobre esta perpendicular. Para la explicación reemplazamos la cara de la moneda por una flecha dirigida hacia arriba. El punto de unión de estas dos monedas también quedaría sobre esta perpendicular Pr el cual en la moneda A sería el punto de inicio p1 y también el punto final p2 del recorrido de la moneda B, y en la moneda B sería el punto p3 que gira al rotarla sobre el perímetro de la moneda A. Esto quiere decir que la distancia recorrida por la moneda B al girarla 360° o una vuelta entera sobre el borde de la moneda A sin perder contacto y sin deslizarse es igual al perímetro de la moneda A, por lo cual al terminar de girarla los 360° esta queda en su posición inicial. La ilusión óptica es que observamos que la moneda gira dos veces sobre su eje mientras que matemáticamente sabemos que, si ambas monedas tienen el mismo tamaño, al tener el mismo perímetro y que el recorrido de la moneda B es igual a este perímetro, matemáticamente deducimos que la moneda en realidad solo gira los 360° una sola vez y no dos. ¿Cómo demostrar que es una ilusión óptica? Si se traza una línea recta horizontal L2 que representaría una superficie plana y tomamos la distancia recorrida o valor del perímetro y la marcamos sobre esta línea horizontal L2 desde el punto inicial p1 hasta el punto final p2, los cuales en este caso no estarán sobrepuestos, y colocamos la moneda B de tal forma que el punto p3 de esta moneda que es el que gira y el punto inicial p1 queden sobrepuestos y el centro de la moneda quede sobre una perpendicular a la línea horizontal L2. Al girar la moneda B los 360° sobre esta línea horizontal L2 sin deslizarse podemos observar que exactamente en la mitad del recorrido la flecha de la moneda queda dirigida hacia abajo. Esta distancia es exactamente la misma recorrida por la moneda B sobre el borde de la moneda A en el momento en que la moneda B queda debajo de la moneda A, razón por la cual la flecha queda dirigida en sentido contrario, o sea hacia arriba.

La ilusión óptica de que la moneda B gira dos veces se genera debido a que el sistema de coordenadas (x, y) de la moneda B también gira 360°, y como por ejemplo si un colombiano en su país estuviera en posición vertical o de pie se comunicara con un chino también ubicado en su país, al preguntarle si el también está de pie y responde afirmativamente, en realidad con respecto al colombiano este está de cabeza.

Referencias[editar]

  1. ↑ Bunch, Bryan H. (1982). Mathematical Fallacies and Paradoxes. Van Nostrand Reinhold. pp. 10–11. ISBN 0-442-24905-5.
  2. ↑ Talwalkar, Presh (5 de julio de 2015). «Everyone Got This SAT Math Question Wrong». MindYourDecisions – via YouTube. 
  3. ↑ «Error found in S.A.T. question». The New York Times (en inglés estadounidense). United Press International. 25 de mayo de 1982. ISSN 0362-4331. Consultado el 9 de febrero de 2021. 

Véase también[editar]

Enlaces externos[editar]

Obtenido de «https://es.wikipedia.org/w/index.php?title=Paradoja_de_la_moneda_que_gira&oldid=159831150»