Método de la secante
En análisis numérico el método de la secante es un método para encontrar los ceros de una función de forma iterativa.
Es una variación del método de Newton-Raphson donde en vez de calcular la derivada de la función en el punto de estudio, teniendo en mente la definición de derivada, se aproxima la pendiente a la recta que une la función evaluada en el punto de estudio y en el punto de la iteración anterior. Este método es de especial interés cuando el coste computacional de derivar la función de estudio y evaluarla es demasiado elevado, por lo que el método de Newton no resulta atractivo.
En otras palabras, el método de la secante es un algoritmo de la raíz de investigación que utiliza una serie de raíces de las líneas secantes para aproximar mejor la raíz de una función f. El método de la secante se puede considerar como una aproximación en diferencias finitas del método de Newton-Raphson. Sin embargo, este método fue desarrollado independientemente de este último.
El método[editar]
El método se define por la relación de recurrencia:
Como se puede ver, este método necesitará dos aproximaciones iniciales de la raíz para poder inducir una pendiente inicial.
Derivación del método[editar]
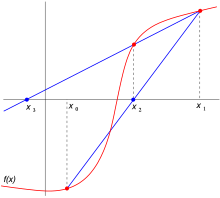
El método se basa en obtener la ecuación de la recta que pasa por los puntos (xn−1, f(xn−1)) y (xn, f(xn)). A dicha recta se le llama secante por cortar la gráfica de la función. En la imagen de arriba a la derecha se toman los puntos iniciales x0 y x1, se construye una línea por los puntos (x0, f(x0)) y (x1, f(x1)). En forma punto-pendiente, esta línea tiene la ecuación mostrada anteriormente. Posteriormente se escoge como siguiente elemento de la relación de recurrencia, xn+1, la intersección de la recta secante con el eje de abscisas obteniendo la fórmula, y un nuevo valor. Seguimos este proceso, hasta llegar a un nivel suficientemente alto de precisión (una diferencia lo suficientemente pequeñas entre xn y xn-1).
Convergencia[editar]
El orden de convergencia de este método, en un punto cercano a la solución, es donde
es el número áureo, por lo que se trata de una convergencia superlineal inferior a la del método de Newton-Raphson. En caso de que la aproximación inicial sea demasiado lejana o la raíz no sea simple, este método no asegura la convergencia y tiene un comportamiento similar al de Newton-Raphson.
Comparación con otros métodos de búsqueda de raíces[editar]
El método de bisección necesita de muchas iteraciones comparado con el método de la secante, ya que el proceso que este sigue es mucho más preciso que el de bisección, el cual solo divide por mitades sucesivamente hasta dar con un valor aproximado al real y por consecuente conlleva un número significativamente mayor de iteraciones.
El método de la regla falsa utiliza la misma fórmula que el método de la secante. Sin embargo, no se aplica la fórmula en xn−1 y xn, como el método de la secante, pero en xn y en la última iteración xk tal que f(xk) y f(xn) tiene un signo diferente. Esto significa que el método de regla falsa siempre converge.
La fórmula de recurrencia del método de la secante se puede derivar de la fórmula para el método de Newton-Raphson:
utilizando la aproximación de diferencias finitas:
Si comparamos el método de Newton-Raphson con el método de la secante, vemos que el método de Newton-Raphson converge más rápido (para 2 en contra α ≈ 1,6). Sin embargo, el método de Newton-Raphson requiere la evaluación de ambos f y su derivada en cada paso, mientras que el método de la secante sólo requiere la evaluación de f. Por lo tanto, el método de la secante puede muy bien ser más rápido en la práctica.
Ejercicio de ejemplo[editar]
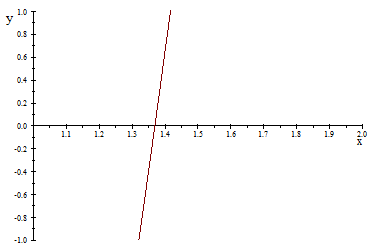
Utilice el método de la secante para encontrar una raíz real de la ecuación polinomial: F(x)=x3+2x2+10x-20=0.
Utilizando la ecuación:
Obtenemos:
Y mediante x0=0 y x1=1 se calcula x2
Los valores posteriores son los siguientes:
| n | xn | |
|---|---|---|
| 0 | 0.00000 | |
| 1 | 1.00000 | 1.00000 |
| 2 | 1.53846 | 0.53846 |
| 3 | 1.35031 | 0.18815 |
| 4 | 1.36792 | 0.01761 |
| 5 | 1.36881 | 0.00090 |
Ahí tenemos el resultado, cuando ≤
Comprobando el resultado graficando la función utilizando software obtenemos:
Si bien no se converge a la raíz tan rápido como resolviéndolo utilizando el método Newton-Raphson, la velocidad de convergencia no es tan lenta como resolviéndolo por el método de punto fijo; entonces se tiene para este ejemplo una velocidad de convergencia intermedia.
Código en Java[editar]
Programa escrito en Java correspondiente al ejemplo f(x) = exp( x ) - ( 2 * x^3 )
public class metodos{
/**
* Este metodo crea un funcion a la cual se le aplicara el método de
* Biseccion teniendo como parametro de entrada un double x, el cual
* sirve para la construccion de la funcion dentro del metodo
* @return
*/
public static double evaluar(double x){
double a = Math.exp( x ) * ( 2*Math.pow( x, 3) );
return a;
}
/**
* Metodo de la Secante el cual le halla las raices de una funciones en un intervalo
* ingresado como parametro de entrada [x1, x2] y un el error con el cual
* deseamos hallar nuestra funcion, y nos retorna la raiz dentro del intervalo
* @param x1
* @param x2
* @param error
* @return x3
*/
public static double secante(double x1, double x2, double error){
double x3, fx1, fx2, fx3;
//string que contendra lal tabla de valores
String line = "";
if ( Math.abs( evaluar( x1 ) ) < Math.abs( evaluar ( x2 ) ) ){
double aux = x1;
x1 = x2;
x2 = aux;
}
fx1 = evaluar( x1 );
fx2 = evaluar( x2 );
do{
x3 = x2 - ( fx2 * ( x1 - x2 ) ) / ( fx1 - fx2 );
fx3 = evaluar( x3 );
line += x1 + " " + x2 + " " + x3 + " " + fx1 + " " + fx2 + " " + fx3 + "\n";
x1 = x2;
x2 = x3;
fx1 = evaluar( x1 );
fx2 = evaluar( x2 );
fx3 = evaluar( x3 );
} while ( Math.abs( fx3 ) > error );
System.out.print( line );
return x3;
}
}
Código en Fortran 90[editar]
Programa escrito en Fortran 90 correspondiente al ejemplo f(x) = x3 + 2x2 + 10x - 20
PROGRAM Metodo_Secante
IMPLICIT NONE
REAL (KIND = 8) :: x0, x1, x, f0, f1, f, tol = 1.0E-3
INTEGER (KIND = 1) :: i, ITER_MAX = 25
EXTERNAL f
x0 = 0. ! aproximación inicial 1
x1 = 1. ! aproximación inicial 2
f0 = f(x0)
f1 = f(x1)
DO i = 2, ITER_MAX
x = x1 - (x1 - x0)*f1/(f1 - f0)
IF (ABS(x - x1).LT.tol) THEN
PRINT*, 'La raíz es:', x, 'en iteración No:', i
EXIT
END IF
x0 = x1
x1 = x
f0 = f1
f1 = f(x)
END DO
IF (i.GT.ITER_MAX) THEN
PRINT*, 'No se halló raíz: cambiar aprox. iniciales o aumentar ITER_MAX'
END IF
END PROGRAM Metodo_Secante
FUNCTION f(x) RESULT (funcion)
IMPLICIT NONE
REAL (KIND = 8) :: funcion, x
INTRINSIC :: cos
funcion = x**3 + 2.*x**2 + 10.*x - 20. ! función
END FUNCTION f
Para compilar en GNU/Linux con compilador de GNU, se escribe en una terminal:
$ gfortran programa.f90 -o programa $ ./programa
Código en Matlab[editar]
Programa escrito en Matlab para ejecutar el método de la secante.
% Una implementación del método de la secante para búsqueda de raices en
% funciones continuas dentro de un intervalo.
%
% Por Gerardo Tinoco Guerrero
%
% Ejemplo:
% Ejecutar las siguientes lineas dentro de la ventana de comandos:
%
% ff = @(x)(x.^2-4)
% x = secante(ff, 1, 5, 0.0001);
%
% Se buscará la raíz de la función (x^2)-4 tomando como puntos iniciales para
% el método de la secante a = 2 y b = 5, con una tolerancia tol = 0.0001.
function xs = secante(fun,a,b,tol)
fprintf('Método de la secante\n\n');
i = 1;
fa = feval(fun, a);
fb = feval(fun, b);
xs = b - ((b - a) / (fb - fa))*fb;
error = abs(b - a);
fprintf('Iter. \t a \t \t b \t \t Xs \n');
fprintf('%2i \t %f \t %f \t %f \n', i, a, b, xs);
while error >= tol
b = a;
a = xs;
fb = feval(fun,b);
fa = feval(fun,a);
xs = b - ((b - a)/(fb - fa))*fb;
error = abs(b - a);
i = i + 1;
fprintf('%2i \t %f \t %f \t %f \n', i, a, b, xs);
end
w = feval(fun,xs);
fprintf('\n La mejor aproximación a la raiz tomando una tolerancia de %f es \n x = %f con \n f(x)=
%f\n y se realizaron %i iteraciones\n',tol, xs, w, i);
end
Alternativa al código anterior.
function y=secant(fun,a,b,tol)
u=subs (fun,a);
v=subs (fun,b);
c=2;
p0=a;
p1=b;
while abs (u)>tol
p=p0-u*(p1-p0)/(v-u);
p0=p;
p1=b;
u=subs(fun,p0);
v=subs(fun,p1);
c=c+1
end
c
p
end
Código en Julia[editar]
Definición de la función:
function secant(f,a,b,rtol,maxIters)
iter = 0
while abs(b-a) > rtol*abs(b) && iter < maxIters
c,a = a,b
b = b + (b-c)/(f(c)/f(b)-1)
iter = iter + 1
end
return b
end
Utilización de la función aplicada al ejercicio propuesto:
secant( x-> x^3+ 2*x^2 +10*x -20, 1, 2, 1e-15, 10 )
1.3688081078213725
Referencias[editar]
Antonio Nieves, Federico C. Domínguez. "Métodos numéricos aplicados a la ingeniería" (Tercera Edición). Editorial Patria.
Enlaces externos[editar]
- Animations for the secant method
- Secant method of zero (root) finding on Mathcad Application Server
- Secant Method Notes, PPT, Mathcad, Maple, Mathematica, Matlab at Holistic Numerical Methods Institute
- Module for Secant Method by John H. Mathews
- [1]