Integral exponencial

En el ámbito de las matemáticas la integral exponencial es una función especial definida en el plano complejo e identificada con el símbolo Ei.
Definiciones[editar]
Para valores reales de , la integral exponencial se define como
Esta definición puede ser utilizada para valores positivos de , pero a causa de la singularidad del integrando en cero, la integral debe ser interpretada en término del valor principal de Cauchy. Para valores complejos del argumento, esta definición es ambigua a causa de los puntos de ramificación en 0 y en .[1] En general, se realiza un corte en el eje real negativo y Ei puede ser definida mediante una continuación analítica en el resto del plano complejo.
Se utiliza la siguiente notación,[2]
Para valores positivos de la parte real de , esto se puede expresar como[3]
El comportamiento de E1 cerca del branch cut puede ser analizado mediante la siguiente relación:[4]
Propiedades[editar]
Las propiedades de la exponencial integral mostradas, en ocasiones, permiten sortear él la evaluación explícita de la función a partir de la definición dada arriba.
Series Convergentes[editar]
Tras integrar la serie de Taylor de , y extraer la singularidad logarítmica, se puede obtener la siguiente representación en forma de serie de para real:[5]
Para argumentos complejos fuera del eje real, esta serie se generaliza a[6]
donde es la constante de Euler-Mascheroni. La suma converge para todo complejo, y tomamos el valor usual del logaritmo complejo con el corte de rama a lo largo del eje real negativo.
Series Asintóticas[editar]
Por desgracia, la convergencia de las series mostradas arriba es muy lenta para argumentos con gran módulo. Por ejemplo, para , se necesitan más de 40 términos para obtener una respuesta correcta con 3 cifras significativas.[7] Sin embargo, existe una serie asintótica divergente que puede ser obtenida a partir de la integración de por partes:[8]
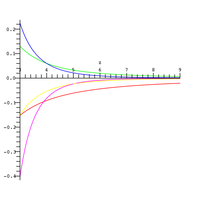
cuyo error es del orden y es válida para grandes valores de . El error relativo de la serie asintótica se muestra en la gráfica de la derecha para varios valores de ( en rojo, en rosa). Cuando , la aproximación dada con es exacta en representación de doble precisión, de 64 bits.
Comportamiento exponencial y logarítmico: Cotas[editar]

De las series dadas arriba, se deduce que se comporta como una exponencial negativa para grandes valores del argumento y como un logaritmo para pequeños valores del mismo. Para valores reales positivos del argumento, queda acotada superior e inferiormente por funciones elementales como sigue:[9]
La parte izquierda de la desigualdad se muestra en la gráfica de la izquierda en azul, la parte central, que es , es la curva negra y la parte de la derecha es la curva roja.
Definición mediante [editar]
Las funciones y pueden ser escritas de forma más simple mediante la función entera [10] definida como
(nótese que esta es la serie alternante que aparecía en la definición de ). Se sigue inmediatamente que:
Relación con otras funciones[editar]
La integral exponencial está altamente relacionada con la función logaritmo integral por la siguiente relación
para valores positivos reales de .
La integral exponencial se puede generalizar a
que es una familia de funciones que puede representarse como un caso especial de la función gamma incompleta:[11]
Esta forma generizada se llama a veces función de Misra function[12] , que se define como
Derivadas[editar]
Las derivadas de las funciones pueden ser obtenerse mediante el uso de la fórmula[13]
Nótese que la función es sencilla de evaluar (dando un término inicial a la relación recursiva), pues es .[14]
Integral Exponencial de argumento imaginario[editar]

Si es imaginario, la función tiene una parte real no nula, así podemos usar la fórmula
para obtener una relación de la exponencial integral con las integrales trigonométricas y :
Las partes real e imaginaria de están dibujadas en la gráfica de la derecha en negro y rojo respectivamente.
Aplicaciones[editar]
- Transmisión de calor con dependencia temporal
- Flujo de aguas subterráneas fuera del equilibrio en la solución de Theis
- Transferencia radiativa en atmósferas estelares
- Ecuación de difusividad radial para flujos transitorios o de flujo no estacionario entre fuentes y sumideros con forma de línea recta.
Referencias[editar]
- ↑ Abramowitz and Stegun, p.228
- ↑ Abramowitz and Stegun, p.228, 5.1.1
- ↑ Abramowitz and Stegun, p.228, 5.1.4 con n = 1
- ↑ Abramowitz and Stegun, p.228, 5.1.7
- ↑ Para una demostración, véase Bender y Orszag, p253
- ↑ Abramowitz y Stegun, p.229, 5.1.11
- ↑ Bleistein y Handelsman, p.2
- ↑ Bleistein y Handelsman, p.3
- ↑ Abramowitz y Stegun, p.229, 5.1.20
- ↑ Abramowitz y Stegun, p.228, véase la nota 3.
- ↑ Abramowitz y Stegun, p.230, 5.1.45
- ↑ After Misra (1940), p.178
- ↑ Abramowitz and Stegun, p.230, 5.1.26
- ↑ Abramowitz and Stegun, p.229, 5.1.24
Véase también[editar]
Bibliografía[editar]
- Abramovitz, Milton; Irene Stegun (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Abramowitz and Stegun. New York: Dover. ISBN 0-486-61272-4.
- Bender, Carl M.; Steven A. Orszag (1978). Advanced mathematical methods for scientists and engineers. McGraw-Hill. ISBN 0-07-004452-X.
- Bleistein, Norman; Richard A. Handelsman (1986). Asymptotic Expansions of Integrals. Dover. ISBN 0486650820.
- Misra, Rama Dhar (1940). «On the Stability of Crystal Lattices. II». Mathematical Proceedings of the Cambridge Philosophical Society 36 (2): 173. doi:10.1017/S030500410001714X.
- Press, William H.; et al (1994). Numerical recipes in C: the art of scientific computing. Cambridge [England]: Cambridge University Press. ISBN 0-521-43108-5. contiene códigos para calcular y , a partir de p.222.
Enlaces externos[editar]
- Weisstein, Eric W. «Exponential Integral». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «En-Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Formulas and identities for Ei














































