Grafo de McGee

Grafo de McGee
	; El Grafo de McGee
Nombre en honor a	W. F. McGee
Vértices	24
Aristas	36
Radio	4
Diámetro	4
Cintura	7
Automorfismos	32
Número cromático	3
Índice cromático	3
Propiedades	Cúbico; Jaula; Hamiltoniano
	[editar datos en Wikidata]

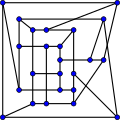
En teoría de grafos, el Grafo de McGee o jaula-(3-7) es un 3-grafo regular de 24 vértices y 36 aristas.^[1]

Es la única (3,7)-jaula (el menor grafo cúbico de girth 7). Es también la menor jaula cúbica que no es un grafo de Moore.

Descubierto por primera vez por Sachs pero no publicado por éste,^[2] el grafo debe su nombre a McGee, quien publicó el resultado en 1960.^[3] Luego Tutte en 1966 demostró que este grafo correspondía a la única jaula-(3,7).^[4]^[5]^[6]

Actualmente se conocen los menores grafos cúbicos con números de cruzamiento 1–8 (sucesión A110507 en OEIS). El menor grafo con cruzamiento 8 es el grafo de McGee. Existen 5 grafos cúbicos no isomórficos de orden 24 con número de cruzamiento 8.^[7] Uno de ellos es el grafo de Petersen generalizado G(12,5), también conocido como el grafo de Nauru.^[8]

El grafo de McGee tiene radio 4, diámetro 4, número cromático 3 e índice cromático 3.

Propiedades algebraicas[editar]

El polinomio característico del grafo de McGee es: $x^{3}(x-3)(x-2)^{3}(x+1)^{2}(x+2)(x^{2}+x-4)(x^{3}+x^{2}-4x-2)^{4}$ .

Galería[editar]

El número de cruce del grafo de McGee es 8.
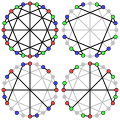
El número cromático del grafo de McGee es 3.
El índice cromático del grafo McGee es 3.
El número cromático acíclico del grafo de McGee es 3.
Dibujo alternativo del grafo de McGee.

Referencias[editar]

↑ ^a ^b ^c ^d ^e ^f Weisstein, Eric W. «McGee Graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
↑ Kárteszi, F. "Piani finit ciclici come risoluzioni di un certo problemo di minimo." Boll. Un. Mat. Ital. 15, 522-528, 1960
↑ McGee, W. F. "A Minimal Cubic Graph of Girth Seven." Canad. Math. Bull. 3, 149-152, 1960
↑ Tutte, W. T. Connectivity in Graphs. Toronto, Ontario: University of Toronto Press, 1966
↑ Wong, P. K. "Cages--A Survey." J. Graph Th. 6, 1-22, 1982
↑ Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance Regular Graphs. New York: Springer-Verlag, p. 209, 1989
↑ Pegg, E. T. and Exoo, G. "Crossing Number Graphs." Mathematica J. 11, 2009
↑ Weisstein, Eric W. «Graph Crossing Number». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

Datos: Q926016
Multimedia: McGee graph / Q926016

[Mathworld-1] ↑ ^a ^b ^c ^d ^e ^f Weisstein, Eric W. «McGee Graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

[2] Kárteszi, F. "Piani finit ciclici come risoluzioni di un certo problemo di minimo." Boll. Un. Mat. Ital. 15, 522-528, 1960

[3] McGee, W. F. "A Minimal Cubic Graph of Girth Seven." Canad. Math. Bull. 3, 149-152, 1960

[4] Tutte, W. T. Connectivity in Graphs. Toronto, Ontario: University of Toronto Press, 1966

[5] Wong, P. K. "Cages--A Survey." J. Graph Th. 6, 1-22, 1982

[6] Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance Regular Graphs. New York: Springer-Verlag, p. 209, 1989

[7] Pegg, E. T. and Exoo, G. "Crossing Number Graphs." Mathematica J. 11, 2009

[8] Weisstein, Eric W. «Graph Crossing Number». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]