Geografía generalizada
En teoría de la complejidad computacional, el juego de geografía generalizada es un conocido problema de PSPACE completo .
Introducción[editar]
El juego de palabras encadenadas o juego de la geografía es un juego para niños, típico para un largo viaje en automóvil, donde los jugadores se turnan para nombrar ciudades de cualquier parte del mundo. Cada ciudad elegida debe comenzar con la misma letra que terminó con el nombre de la ciudad anterior. La repetición no está permitida. El juego comienza con una ciudad de inicio arbitraria y termina cuando un jugador pierde porque no puede continuar.
Modelo usando grafos[editar]
Para visualizar el juego, se puede construir un grafo dirigido cuyos nodos son cada ciudad del mundo. Se agrega una flecha desde el nodo N1 al nodo N2 si y solo si el etiquetado de la ciudad N2 comienza con la letra que termina el nombre del nodo de etiquetado de la ciudad N1 . En otras palabras, dibujamos una flecha de una ciudad a otra si la primera puede conducir a la segunda de acuerdo con las reglas del juego. Cada borde alternativo en el gráfico dirigido corresponde a cada jugador (para un juego de dos jugadores). El primer jugador que no puede extender el camino pierde. En la figura a continuación se muestra una ilustración del juego (que contiene algunas ciudades de Míchigan).
En un juego de geografía generalizada (GG), reemplazamos el gráfico de nombres de ciudades con un gráfico arbitrario dirigido. El siguiente gráfico es un ejemplo de un juego de geografía generalizada.
Jugando el juego[editar]
Definimos P1 como el jugador que se mueve primero y P2 como el jugador que se mueve segundo y nombramos los nodos N1 a Nn . En la figura anterior, P1 tiene una estrategia ganadora de la siguiente manera: N1 apunta solo a los nodos N2 y N3 . Por lo tanto, el primer movimiento de P1 debe ser una de estas dos opciones. P1 elige N2 (si P1 elige N3, entonces P2 elegirá N9 ya que esa es la única opción y P1 perderá). Luego P2 elige N4 porque es la única opción restante. P1 ahora elige N5 y P2 elige posteriormente N3 o N7. Independientemente de la opción de P2, P1 elige N9 y P2 no tiene opciones restantes y pierde el juego.
Complejidad computacional[editar]
El problema de determinar qué jugador tiene una estrategia ganadora en un juego de geografía generalizado es completo para PSPACE .
Geografía generalizada está en PSPACE[editar]
Sea GG = {<G, b> | P1 tiene una estrategia ganadora para el juego de geografía generalizado en el grafo G a partir del nodo b }. Para mostrar que GG ∈ PSPACE, presentamos un algoritmo recursivo de espacio polinómico que determina qué jugador tiene una estrategia ganadora. Dada una instancia de GG, <G, nstart> donde G es un grafo dirigido y nstart es el nodo de inicio designado, el algoritmo M procede de la siguiente manera:
En M(<G,nstart>):
- Medir la cantidad de sucesores del nodo nstart. Si es 0, entonces rechazar, porque no hay movimientos disponibles para el jugador uno.
- Construir una lista de todos los nodos alcanzables desde nstart por una arista: n1, n2, ..., ni.
- Eliminar nstart y todas las aristas bordes conectados a él en G para formar G1.
- Para cada nodo nj en la lista n1, ..., ni, llamar a M(<G1, nj>).
- Si todas estas llamadas son aceptadas, no importa qué decisión tome P1, P2 tiene una estrategia para ganar, por lo que esta llamada rechaza. De lo contrario (si una de las llamadas rechaza) P1 tiene una opción que evitará cualquier estrategia exitosa para P2, así que acepta.
El algoritmo M claramente decide GG. Está en PSPACE porque el único espacio de trabajo polinómico no obvio consumido está en la pila de recursión. El espacio consumido por la pila es polinomial porque cada nivel agrega un solo nodo a la pila, y hay a lo sumo n niveles, donde n es el número de nodos en G.
Geografía generalizada es PSPACE-hard[editar]
La siguiente prueba se debe a David Lichtenstein y Michael Sipser.[1]
Para establecer que GG es PSPACE-hard, podemos reducir el problema del juego de fórmulas (que se sabe que es PSPACE-hard) a GG en tiempo polinómico (P). En resumen, una instancia del problema FORMULA-GAME consiste en una fórmula booleana cuantificada φ = ∃x1∀x2∃x3...Qxk(ψ) donde Q es ∃ o ∀. El juego es jugado por dos jugadores, Pa y Pe, que alternan eligiendo valores para sucesivos xi . Pe gana el juego si la fórmula ψ termina siendo verdadera, y Pa gana si ψ termina siendo falsa . Se supone que la fórmula ψ está en forma normal conjuntiva.
En esta prueba, suponemos que la lista de cuantificadores comienza y termina con el calificador existencial, ∃, por simplicidad. Tenga en cuenta que cualquier expresión se puede convertir a este formulario agregando variables tontas que no aparecen en ψ.
Al construir un grafo G como el que se muestra arriba, mostraremos que cualquier instancia del juego de las fórmulas puede reducirse a una instancia de geografía generalizada, donde la estrategia óptima para P1 es equivalente a la de Pe, y la estrategia óptima para P2 es equivalente a la de Pa.
La cadena vertical izquierda de nodos está diseñada para imitar el procedimiento de elegir valores para variables en el juego de las fórmulas. Cada estructura de diamante corresponde a una variable cuantificada. Los jugadores se turnan para decidir caminos en cada ramificación. Como asumimos que el primer cuantificador sería existencial, P1 va primero, seleccionando el nodo izquierdo si x1 es verdadero y el nodo derecho si x1 es falso. Cada jugador debe tomar turnos forzados, y luego P2 elige un valor para x2 . Estas asignaciones alternas continúan por el lado izquierdo. Después de que ambos jugadores pasan por todos los diamantes, nuevamente es el turno de P1, porque asumimos que el último cuantificador es existencial. P1 no tiene más remedio que seguir el camino hacia el lado derecho del gráfico. Entonces es el turno de P2 para hacer un movimiento.
Cuando el juego llega al lado derecho del gráfico, es similar al final del juego en el juego de las fórmulas. Recuerde que en el juego de las fórmulas, Pe gana si ψ es verdadero, mientras que Pa gana si ψ es falso. El lado derecho del gráfico garantiza que P1 gana si y solo si Pe gana, y que P2 gana si y solo si Pa gana.
Primero mostramos que P2 siempre gana cuando Pa gana. Si Pa gana, ψ es falso. Si ψ es falso, existe una cláusula insatisfacible. P2 elegirá una cláusula insatisfacible para ganar. Luego, cuando es el turno de P1, debe elegir un literal en esa cláusula elegida por P2. Como todos los literales en la cláusula son falsos, no se conectan a los nodos visitados previamente en la cadena vertical izquierda. Esto permite que P2 siga la conexión al nodo correspondiente en un diamante de la cadena izquierda y lo seleccione. Sin embargo, P1 ahora no puede seleccionar ningún nodo adyacente y pierde.
Ahora mostramos que P1 siempre gana cuando Pe gana. Si Pe gana, ψ es verdadera. Entonces cada cláusula en el lado derecho del gráfico contiene un literal verdadero. P2 puede elegir cualquier cláusula. Entonces P1 elige el literal que es verdadero. Y debido a que es cierto, su nodo adyacente en el nodo vertical izquierdo ya ha sido seleccionado, por lo que P2 no tiene movimientos que realizar y pierde.
Geografía generalizada planar es PSPACE completa[editar]
La geografía generalizada es PSPACE completa, incluso cuando se juega en grafos planares . La siguiente prueba es del teorema 3 de.[1]
Dado que GG plano es un caso especial de GG, y GG está en PSPACE, GG plano está en PSPACE. Queda por demostrar que el GG plano es PSPACE-hard. Esto se puede demostrar mostrando cómo convertir un gráfico arbitrario en un gráfico plano, de modo que un juego de GG jugado en este gráfico tendrá el mismo resultado que en el gráfico original.
Para hacer eso, solo es necesario eliminar todos los cruces de bordes del gráfico original. Dibujamos el gráfico de tal manera que no se crucen tres aristas en un punto, y no se pueden usar dos aristas cruzadas en el mismo juego. Esto no es posible en general, pero siempre es posible para el grafo construido a partir de una instancia del juego de las fórmulas; por ejemplo, podríamos tener solo los bordes de los vértices de la cláusula involucrados en los cruces. Ahora reemplazamos cada cruce con esta construcción:
El resultado es un gráfico planar, y el mismo jugador puede forzar una victoria como en el gráfico original: si un jugador elige moverse "hacia arriba" desde V en el juego transformado, ambos jugadores deben continuar moviéndose "hacia arriba" a W o perder inmediatamente. Entonces, moverse "hacia arriba" desde V en el juego transformado simula el movimiento V → W en el juego original. Si V → W es un movimiento ganador, entonces moverse "hacia arriba" desde V en el juego transformado también es un movimiento ganador, y viceversa.
Por lo tanto, el juego de GG jugado en el gráfico transformado tendrá el mismo resultado que en el gráfico original. Esta transformación lleva un tiempo que es un múltiplo constante del número de intersecciones de aristas en el gráfico original, por lo que lleva tiempo polinomial.
Por lo tanto, GG planar es PSPACE completo.
Gráfico bipartito plano con grado máximo 3[editar]
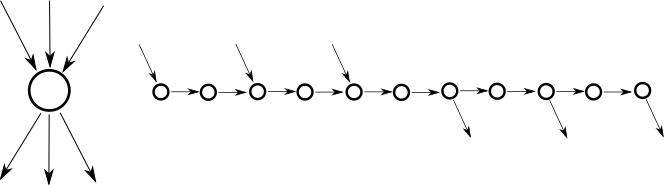
GG jugado en gráficos bipartitos planares con un grado máximo 3 todavía es completo en PSPACE, reemplazando los vértices de grado superior a 3 con una cadena de vértices con grado como máximo 3. La prueba está en.[1] Básicamente,
Geografía de aristas[editar]
Una variante de GG se llama geografía de aristas, donde después de cada movimiento, el borde por el que pasó el jugador se borra. Esto está en contraste con el GG original, donde después de cada movimiento, se borra el vértice en el que solía estar el jugador. En esta vista, el GG original se puede llamar geografía de vértices.
La geografía de aristas es PSPACE completa. Esto se demuestra al reducir un problema de decisión de fórmulas booleanas cuantificadas a la geografía de aristas.[2]
Grafos no dirigidos[editar]
También se puede considerar jugar cualquier juego de Geografía en un gráfico no dirigido (es decir, los bordes se pueden atravesar en ambas direcciones). Fraenkel, Scheinerman y Ullman[3] muestran que la geografía de vértices no dirigidos se puede resolver en tiempo polinómico, mientras que la geografía de aristas no dirigida es PSPACE completa, incluso para grafos planares con grado máximo 3. Si el gráfico es bipartito, entonces la Geografía de aristas no dirigida es solucionable en tiempo polinomial.
Consecuencias[editar]
Dado que GG es PSPACE completo, no existe un algoritmo de tiempo polinómico para un juego óptimo en GG a menos que P = PSPACE. Sin embargo, puede que no sea tan fácil demostrar la complejidad de otros juegos porque ciertos juegos (como el ajedrez ) contienen un número finito de posiciones de juego — lo que hace difícil (o imposible) formular un mapeo a un problema de PSPACE completo. A pesar de esto, la complejidad de ciertos juegos aún puede analizarse mediante generalización (p. Ej., En un tablero n × n ). Vea las referencias para una prueba de Go generalizada, como corolario de la prueba de la integridad de GG.
Referencias[editar]
- ↑ a b c Lichtenstein, David; Sipser, Michael (April 1980). «Go Is Polynomial-Space Hard». Journal of the ACM 27 (2): 393-401. doi:10.1145/322186.322201.
- ↑ Schaefer, Thomas J. (1978). «On the complexity of some two-person perfect-information games». Journal of Computer and System Sciences 16 (2): 185-225. doi:10.1016/0022-0000(78)90045-4.
- ↑ Fraenkel, Aviezri; Scheinerman, Edward; Ullman, Daniel (1993). «Undirected edge geography». Theoretical Computer Science 112 (2): 371-381. doi:10.1016/0304-3975(93)90026-p.
- Michael Sipser, Introduction to the Theory of Computation, PWS, 1997.
- David Lichtenstein y Michael Sipser, GO is polynomial Space Hard, Journal of the Association for Computing Machinery, abril de 1980. [1] [2]




