Diferencia entre revisiones de «Teorema del transporte de Reynolds»

← Ir a diferencia anterior Ir a siguiente diferencia →

Contenido eliminado Contenido añadido

En renglón

Revisión del 20:45 16 sep 2009

El teorema de transporte de Reynolds relaciona, la derivada Lagrangiana de una integral de volumen de un sistema, con una integral en derivadas Eulerianas. En otras palabras, este teorema relaciona la tasa de cambio en el tiempo de una propiedad extensiva $\mathrm {H}$ con la generación y el flujo de la propiedad intensiva correspondiente $\eta$ , una y otra relacionadas por la ecuación:

$\mathrm {H} =\left(\int _{V}\rho \eta dV\right)$

La expresión general de este teorema es:

${\frac {D\mathrm {H} }{Dt}}={\frac {\partial }{\partial t}}\left(\int _{V}\rho \eta dV\right)+\int _{s}{\vec {U}}\rho \eta {\hat {n}}dS$

Demostración

Consideremos un sistema en dos instantes de tiempo t y t+ Archivo:DT.jpg. Sea α alguna propiedad por unidad de volumen. El sistema puede tener un cambio de volumen y posición como se muestra en la figura:

La cantidad total de la propiedad α en el sistema en el instante t es:

Archivo:2frea.jpg

Y la cantidad de α en el instante t+ Archivo:DT.jpg es:

Archivo:3frea.jpg

La derivada material de la cantidad total de α en el sistema se puede expresar:

Archivo:4frea.jpg

Que se obtiene de la definición de derivada:

Archivo:5frea.jpg

En esta ecuación:

Archivo:6frea.jpg

Representa el integrando fijo con cambio de volumen como se muestra en la figura:

Y estas dos integrales se pueden reducir a:

Archivo:8frea.jpg

Si consideramos que un elemento dS de la superficie del sistema tiene dos posiciones diferentes en los dos instantes de tiempo considerados t y t+ Archivo:DT.jpg, el barrido de ésta superficie entre los dos instantes conforma el elemento de volumen dV como se muestra en la figura:

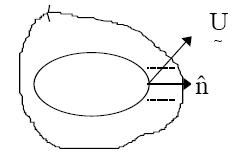
Si Archivo:NGORRO.jpg es el vector normal a la superficie y Archivo:UGUION.jpg representa la velocidad, Archivo:UXN.jpg será la velocidad normal a la superficie. En el tiempo la superficie se mueve una distancia Archivo:UXNdt.jpg normal a la misma. Por lo que:

Archivo:10frea.jpg

La integral se reduce a la integral sobre la superficie:

Archivo:11frea.jpg

Tomando el límite se simplifica a:

Archivo:12frea.jpg

Aplicando el teorema de Gauss esta integral toma la forma:

Archivo:13frea.jpg

Dos términos de la ecuación pueden simplificarse como:

Archivo:14frea.jpg

Con estas simplificaciones toma la forma:

Archivo:15frea.jpg

En notación indical:

Archivo:16frea.jpg

@@ Línea 1: / Línea 1: @@
 {{wikificar|física|t=20071204101825}}
-'''El teorema de transporte de ANDRES LARA''' relaciona, la [[derivada Lagrangiana]] de una [[integral]] de volumen de un sistema, con una [[integral en derivadas Eulerianas]]. En otras palabras, este teorema relaciona la tasa de cambio en el tiempo de una propiedad extensiva <math>\Eta</math> con la generación y el flujo de la propiedad intensiva correspondiente <math>\eta</math>, una y otra relacionadas por la ecuación:
+'''El teorema de transporte de Reynolds''' relaciona, la [[derivada Lagrangiana]] de una [[integral]] de volumen de un sistema, con una [[integral en derivadas Eulerianas]]. En otras palabras, este teorema relaciona la tasa de cambio en el tiempo de una propiedad extensiva <math>\Eta</math> con la generación y el flujo de la propiedad intensiva correspondiente <math>\eta</math>, una y otra relacionadas por la ecuación:
 <math>