Integral de Riemann

La integral de Riemann es una operación sobre una función continua y limitada en un intervalo [a; b], donde a y b son llamados los extremos de la integración. La operación consiste en hallar el límite de la suma de productos entre el valor de la función en un punto x_i* y el ancho Δx del subintervalo conteniendo al punto.

$\lim _{n\to \infty }\sum _{i=0}^{n-1}f(x_{i}^{*})\Delta x_{i}$

Donde n es la cantidad de subintervalos.

Normalmente se nota como:

$\int _{a}^{b}f(x)dx$

El símbolo $\int ,$ es una "S" deformada. En el caso en que la función f tenga varias variables, el dx especifica la variable de integración.
Si la variable de integración y el intervalo de integración son conocidos, la notación se puede simplificar como $\int f$.

Algunas funciones no son claramente integrables por Riemann, pero en general las interacciones de los límites con la integral de Riemann son difíciles de estudiar.

La integral de Lebesgue mejora esta teoría y permite obtener una mayor variedad de funciones integrables, así como describir mejor las interacciones de los límites con la integral.

Históricamente, Riemann concibió esta teoría de integración, y proporcionó algunas ideas para el teorema fundamental del cálculo diferencial e integral. La teoría de la integración de Lebesgue llegó mucho más tarde, cuando los puntos débiles de la integral de Riemann se comprendían mejor.

Interpretación geométrica

En Análisis real, la integral de Riemann es una forma simple de definir la integral de una función sobre un intervalo como el área bajo la curva de la función.

Sea f una función con valores reales definida sobre el intervalo [a, b], tal que para todo x, f(x)≥0 (es decir, tal que f es positiva). Sea S = S_f={(x, y)|0≤y≤f(x)} la región del plano delimitada por la curva correspondiente a la función f, el eje de las abscisas y las rectas verticales de ecuaciones x=a y x=b. Estamos interesados en medir el área del dominio S, si es que se puede medir.

figura 1

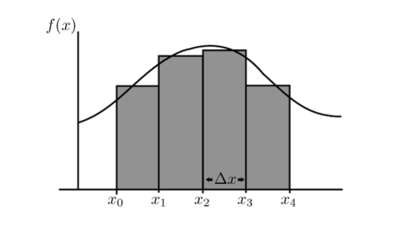
Para obtener una aproximación al área encerrada debajo de una curva, se la puede dividir en rectángulos como indica la figura.

figura 2

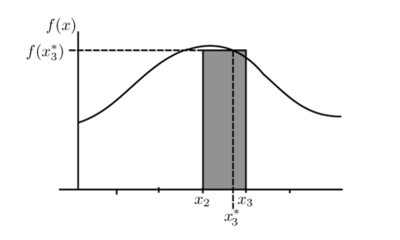
El área de cada rectángulo, es el producto de la función en un punto, por el ancho del intervalo.

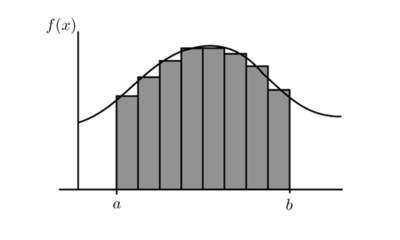
Al aumentar el número de rectángulos se obtiene una mejor aproximación.

figura 3

figura 4

La idea fundamental de la teoría de la integración de Riemann es la de utilizar aproximaciones del área del dominio S. Determinaremos un área aproximada de la que estamos seguros de que son inferiores al área del dominio S, y buscaremos un área aproximada que sepamos que es mayor al área de S. Si estas aproximaciones pueden hacerse de forma que la diferencia entre ambas puede hacerse arbitrariamente pequeña, entonces podemos obtener el área del dominio S. Por lo tanto, el límite del área para infinitos rectángulos es el área comprendida debajo de la curva.

Enlaces externos

• Integral de Riemann (Departamento de Matemática Aplicada. Facultad de Informática de la Universidad Politécnica de Madrid)

• Integral definida (Manuel Sada Allo): Ejemplo 1 Ejemplo 2