Espacio de color Lab
Lab es el nombre abreviado de dos espacios de color diferentes. El más conocido es CIELAB (estrictamente CIE 1976 L*a*b*) y el otro es Hunter Lab (estrictamente, Hunter L, a, b)[1]. Lab es una abreviación informal, y puede confundirse con uno u otro espacio de color. Los espacios de color están relacionados en intención y propósito, pero son diferentes.
Ambos espacios son derivados del espacio "maestro" CIE 1931 XYZ. Sin embargo, CIELAB se calcula usando raíces cúbicas, y Hunter Lab se calcula usando raíces cuadradas.[2] Se recomienda utilizar CIELAB para nuevas aplicaciones, excepto donde los datos deban compararse con valores Hunter L,a,b existentes.[2]
El propósito de ambos espacios es producir un espacio de color que sea más "perceptivamente lineal" que otros espacios de color. Perceptivamente lineal significa que un cambio de la misma cantidad en un valor de color debe producir un cambio casi de la misma importancia visual. Lo anterior puede mejorar la reproducción de tonos cuando se almacenan colores en valores de precisión limitada. Ambos espacios Lab están relacionados con el punto-blanco de los datos XYZ desde donde fueron convertidos. Los valores Lab no definen colores absolutos a no ser que se especifique el punto-blanco. En la práctica, muchas veces se asume que el punto-blanco sigue un estándar y no se establece explícitamente (por ejemplo, todos los valores Lab ICC son relativos al iluminante D50 del estándar CIE).
Las siglas LAB se refieren al espacio de color tridimensional, en donde L o L* es luminosidad de negro a blanco, A o a* va de rojo a verde y B o b* va de azul a amarillo. Actualmente se usa en Adobe Photoshop, perfiles ICC, archivos TIFF y documentos PDF.
Ventajas de LAB[editar]

Comparado con el RGB y CMYK, a menudo es más rápido hacer correcciones eficientes de color en Lab. El hecho de que la luminosidad es completamente ignorada en los canales A y B, hace que sea mucho menos sensible a errores.
Aunque el número de valores numéricos posibles por cada píxel es menor en Lab que en RGB o CMYK, es posible referenciar una cantidad superior de colores en total desde el sistema Lab -no solo colores que no pueden ser descritos con RGB o CMYK sino también colores que no aparecen en absoluto en el mundo real. En algunos casos este acceso a colores imaginarios es de utilidad cuando se generan manipulaciones de imagen de gran cantidad de pasos.
Sería natural asumir que uno pierde información convirtiendo una imagen entre Lab y cualquier otro espacio de color. De todas maneras, de acuerdo a las pruebas realizadas por Dan Margulis, la pérdida es mínima.[3]
Significado de "LAB"[editar]
Algunos usos específicos de la abreviación en literatura, software, etc.
- En Adobe Photoshop, la edición de imágenes usando "Lab" es CIELAB D50.
- En Perfiles ICC, el espacio de color Lab usado como el espacio de conexión de perfil es CIELAB D50.
- En archivos TIFF, el espacio de color Lab es CIELAB.
- En documentos PDF, Lab es CIELAB.
El espacio de color CIE 1976 L*, a*, b* CIELAB)[editar]
El CIE L*a*b* (CIELAB) es el modelo cromático usado normalmente para describir todos los colores que puede percibir el ojo humano. Fue desarrollado específicamente con este propósito por la Commission Internationale d'Eclairage (Comisión Internacional de la Iluminación), razón por la cual se abrevia CIE. Los asteriscos (*) que siguen a cada letra forman parte del nombre, ya que representan L*, a* y b*, de L, a y b [1].
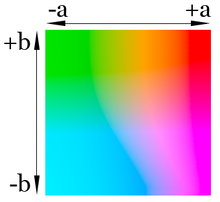
Los tres parámetros en el modelo representan la luminosidad de color (L*, L*=0 rendimientos negro y L*=100 indica blanca), su posición entre rojo y verde (a*, valores negativos indican verde mientras valores positivos indican rojo) y su posición entre amarillo y azul (b*, valores negativos indican azul y valores positivos indican amarillo).
El modelo de color Lab ha sido creado para servir como referencia, independiente del dispositivo utilizado . Por eso, las representaciones visuales de la plena gama de colores en este modelo nunca son exactas. Están ahí solo para ayudar en el concepto, pero son intrínsecamente inexactas.
El modelo de color Lab es tridimensional y solo puede ser representado adecuadamente en un espacio tridimensional.
 |
 |
Diferencias de medida[editar]
CIE 1976 L*a*b* está basado en el espacio de color XYZ CIE 1931 como un intento de linealizar las diferencias de color perceptibles por el ojo humano, usando la métrica de diferencias de color descritas por la elipse de MacAdam. Las relaciones no lineales para L*, a* y b* pretenden emular la respuesta no lineal del ojo. Además, los cambios uniformes de los componentes en el espacio de color L*a*b* tienen por objeto corresponder a cambios uniformes en el color percibido, por lo que las diferencias relativas de percepción entre dos colores en el espacio L*a*b* se pueden aproximar tratando cada color como un punto en un espacio tridimensional, con tres componentes: L *, a *, b * y tomando la distancia entre ellos.
Conversiones RGB y CMYK[editar]
No existen fórmulas sencillas para la conversión entre valores RGB o CMYK y L*a*b*, ya que los modelos de color RGB y CMYK dependen del dispositivo. Los valores RGB o CMYK deben ser transformados a un espacio de color absoluto específico, tal como sRGB o RGB de Adobe. Estos espacios serán dependientes del dispositivo, a diferencia de los datos resultantes de la transformación, permitiendo que estos datos sean transformados al espacio de color CIE 1931 y luego en L*a*b*.
Conversiones XYZ a CIE L*a*b* (CIELAB) y viceversa[editar]
Transformación directa[editar]
donde
Donde , y son los valores triestímulo CIE XYZ del punto de blanco de referencia.
La división de la función f(t) en dos dominios se hace para prevenir una pendiente infinita en t=0. Se asume que la función f(t) sea lineal para un tiempo t=t0 y que coincide con la raíz cúbica de t para t=t0, tanto en valor como en pendiente. En otras palabras, esto se puede expresar como:
El valor de b fue ajustado a 16/116. Las anteriores ecuaciones pueden ser resueltas para a y t0:
donde δ = 6/29. Nótese que
Transformación inversa[editar]
La transformación inversa es como sigue, con como se mencionó antes:
Conversiones XYZ a CIELUV y viceversa[editar]
Transformación Inversa[editar]
La Transformada desde (u',v') a (x,y) es:
- .
La Transformación de CIELUV a XYZ se lleva a cabo como sigue:
Espacio de Color de Hunter Lab[editar]
La variable L es una correlación de la luminosidad, y es calculada a partir del valor Y triestímulo usando la Aproximación de Priest para el valor de Munsell:
donde Yn es el valor Y tri-estímulo de un objeto blanco específico. Para aplicaciones de color de superficie, el objeto blanco específico generalmente es (aunque no siempre) un material hipotético con reflectancia unitaria que cumple con la Ley de Lambert-Beer. El resultado es que el valor de L estará comprendido en una escala entre 0 (negro) y 100 (blanco); aproximadamente 10 veces el valor de Munsell. Nótese, sin embargo, que una luminosidad de 50 no se produce por un valor Y de 50, sino de 25.
Las ecuaciones que siguen muestran los valores a y b, los cuales son los valores de los denominados ejes de colores complementarios. que representan aproximadamente los componentes de rojo (positivo) y verde (negativo) y se calculan de esta manera:
en la cual es un coeficiente que depende de la fuente luminosa (para D65, es 172,30; ver la fórmula aproximada más adelante) y Xn es el valor triestímulo del objeto blanco especificado.
El valor b, es positivo para los amarillos y negativo para las tonalidades azules y se calcula así:
es un coeficiente que también depende de la fuente luminosa (para D65, es 67,20) y Zn es el valor triestímulo Z del objeto blanco especificado.[4]
Ambos valores serán cero para los objetos que tienen idénticas coordenadas de cromaticidad a los objetos blancos específicos. Por lo general, este es el caso de los colores neutrales.
Fórmulas Aproximadas para y [editar]
En la versión anterior del espacio de color de Hunter Lab, valía 175 y , 70. Al parecer, Hunter Lab descubrió que un mejor acuerdo se podría obtener con otras mediciones de diferencia de color, como CIELAB, permitiendo que estos coeficientes dependan del alumbrado. Las fórmulas aproximadas son:
que dan lugar a los valores originales de la iluminación C, que fue la que se usó originalmente en el espacio de color Lab.
El Espacio de Color Hunter Lab como un Espacio de color de valencia cromática de Adams[editar]
Los espacios de color de valencia cromática de Adams están basados en dos elementos: una escala relativa de luminosidad uniforme, y una escala relativa de cromaticidad uniforme.[5] Si se toma la aproximación de Priest de la escala de luminosidad uniforme respecto al valor de la escala de Munsell, esta podría ser expresada en notación moderna como sigue:
y como las coordenadas de cromaticidad uniforme:
donde es un coeficiente de ajuste, se obtienen los valores de los dos ejes cromáticos:
y
la cual es idéntica a las fórmulas de Hunter Lab suministradas anteriormente si se elige a y . Por lo tanto, el espacio de color Hunter Lab es un espacio de color de valencia cromática de Adams.
Diferencia de color[editar]
La llamada “Diferencia de color CIE-LAB” (ΔE*), cuantifica numéricamente la diferencia de percepción de color, para el ojo humano. El término E de ΔE* deriva del vocablo alemán Empfindung, que significa sensación, por lo que ΔE* significa literalmente diferencia de sensación; el asterisco se usa para denotar que estas diferencias han sido calculadas a partir del Sistema CIE-LAB. De acuerdo con la representación tridimensional de este sistema, si dos puntos en éste espacio (representados por dos estímulos de color, “r” y “s”), son coincidentes, entonces la diferencia cromática entre ambos estímulos es igual a cero. Según se incrementa la distancia entre esos dos puntos (L*r, a*r, b*r y L*s, a*s, b*s), es razonable suponer que aumentará la percepción de diferencia cromática entre los estímulos que ambos puntos representan. Una forma de medir la diferencia cromática entre dos estímulos es, por tanto, medir la distancia euclidiana o pitagórica ΔE*, existente entre dos puntos en un espacio tridimensional, donde el valor ΔE* representa la hipotenusa de un triángulo, siendo ΔL* y ΔC* los catetos. Los valores de ΔE* obtenidos para una muestra en referencia al estándar permiten evidenciar si el observador podrá o no percibir la diferencia de color. En la tabla 1, se presenta la relación entre el juicio del observador y ΔE* [1].
| Tabla 1. Relación entre el juicio del observador y la diferencia de color ΔE* [1] | |
| Diferencia percibida sensorialmente | Valor de ΔE* (instrumentalmente) |
| Ninguna | 0 - 0.7 |
| Ligera | 0.7 – 2.5 |
| Notable | 2.5 - 3.0 |
| Apreciable | 3.0 - 6.0 |
| Considerable | 6.0 - 12.0 |
| Extraordinaria | 12.0 |
Referencias[editar]
- ↑ a b c d
- ↑ a b Hunter L,a,b Versus CIE 1976 L*a*b* Archivado el 28 de septiembre de 2007 en Wayback Machine. (PDF)
- ↑ Dan Margulis (2006). Photoshop Lab Color: The Canyon Conundrum and Other Adventures in the Most Powerful Colorspace, ISBN 0-321-35678-0.
- ↑ Hunter Labs (1996). "Hunter Lab Color Scale". Insight on Color 8 9 (August 1-15, 1996). Reston, VA, USA: Hunter Associates Laboratories.
- ↑ Adams, E. Q. (1942). "X-Z planes in the 1931 I.C.I. system of colorimetry". JOSA 32 3: 168-173.

![{\displaystyle {\begin{aligned}L^{\star }&=116f(Y/Y_{n})-16\\a^{\star }&=500\left[f(X/X_{n})-f(Y/Y_{n})\right]vv\\b^{\star }&=200\left[f(Y/Y_{n})-f(Z/Z_{n})\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5d8111caac9fe75eac88b42e748c7381a106be8)





























