Discusión:Función continua

Que ocurre con la función

$f(x)=1/(exp(1/x)+1)$

Esta función es discontinua en $x=0$ con

lim f(x) = 1

x->0(-)

lim f(x) = 0

x->0(+)

por tanto, $f(0)$ no existe.

Su derivada

$g(x)=f'(x)=exp(1/x)/((exp(1/x)+1)*x)^{2}$ sí tiene límite en $x=0$

lim g(x)=0

x->0

Aunque no està definida en $g(0)$, se puede definir $g(0)=0$.

Contradice el teorema?

Estilo de las definiciones

Por cuestión de estilo, en las definiciones se pone si y en los teoremas si y solo si

Por ejemplo:

Definición: una función es continua si la anti-imagen de cada abierto es un abierto.

Teorema: una función es continua si y solo si la anti-imagen de cada entorno es un entorno.

Respuesta a la cuestión de f(x)=x/(exp(1/x)+1)

La respuesta es no. Como bien dices, no existe g(0). Se puede definir g(0), pero entonces tienes OTRA función, no la misma.

Por otra parte, tú estás trabajando sobre la derivada de la función, no sobre la función. El teorema dice que si una función es derivable en un punto, entonces ESA MISMA FUNCIÓN es continua en el mismo punto. Nada dice de la derivada de la función, ni sobre su continuidad.

Por último, Teorema de Gödell aparte, no se puede encontrar un contraejemplo a un teorema. No sería un teorema.

Punto de vista general

El artículo, tal y como está ahora es un resumen de un curso sobre continuidad de funciones reales de variable real. Voy a cogerlo entero y meterlo en un apartado que se llame precisamente así (coninuidad de funciones reales de variable real), para poder dar cabida a otros tipos de funciones (variable compleja, varias variables, operadores, funcionales, aplicaciones continuas entre espacios topológicos en general...).

Fusionar con "Continuos"

He fusionado el artículo Continuos a éste. Copio aquí su discusión:

Discusión en "Continuos"

Revisar la posible fusión con el artículo Continuidad (matemáticas).Joseaperez 08:00 25 nov, 2004 (CET)

Sobre el término Continuo

Desde el punto de vista matemático, el término continuo sólo tiene sentido propio cuando se refiere a un conjunto compacto y conexo. Buena parte de la gente confunde continuo con conexo (véase el artículo continuo). El único otro uso que se le da matemáticamente (en castellano) a la palabra es para hablar de cierto tipo de funciones cointinuas, cuando la función tiene, en castellano, un nombre masculino: por ejemplo, se habla de funcionales continuos, de operadores continuos, etc. Pero no es una definición independiente del de función continua, sino que es EXACTAMENTE LA MISMA. Así pues, el término correcto en castellano es "función continua", o si queremos, "continua".

A mi parecer, toda la información que se encuantra en éste artículo puede ser incorporada a la sección de "Funciones reales de una variable real continuas" del artículo "Continuidad (Matemáticas)", por dos razones: se centraliza mejor la información (actualmente parte de la información que aparece en éste artículo no se encuantra en aquél) y porque es el que lleva el nombre correcto desde el punto de vista matemático.

Procedo a copiar allí toda la información no redundante que aparece aquí.

Sobre definición de continuidad

Creo que no es correcto definir la continuidad en términos de límites, sobre todo porque la continuidad tiene mucho que ver con el hecho de que haya un límite. En efecto, cuando hablamos de límites por la derecha o por la izquierda que se "acercan" a un punto, estamos suponiendo que la función es continua en intervalos cercanos a dicho punto, quizás sin incluirlo.

La definición propia es la siguiente. Sea f una función (real de variable real, se entiende) definida en un intervalo (a,b), y sea c un punto en el dominio de f. Decimos que f es continua en el punto c, si para todo e>0, existe una d>0 tal que |x-c|<d ==> |f(x)-f(c)|<e. Si existe tal d que implique al consecuente anterior, decimos que f es continua en c.

La discontinuidad se define como la negación de la implicación anterior. Saludos.

---

Hola:

No es cierto lo que dices de que se suponga que la función es continua en intervalos cercanos a un punto cuando definimos la continuidad mediante límites. Si bien es cierto que, estrictamente hablando, la definición de continuidad es exactamente aquella que tú mencionas, ésta es totalmente equivalente a la definición por límites. La razón es un poco técnica, pero sencilla (es decir, que requiere conocimientos serios de Topología, pero en esos términos es muy sencilla de entender): se dice que $y_{0}$ es punto límite de $f$ en $x_{0}$ si $y_{0}$ es punto límite de la base de filtro que se obtiene al tomar las imágenes de la base de filtro formada por los entornos del punto $x_{0}$. Traduciendo el lenguaje de entornos al lenguaje de distancias (valor absoluto) se obtiene la definición que mencionas.

Para ver que no se supone continuidad de la función mediante la definición por límites, puedes comprobar que la función: $f:\mathbb {R} \longrightarrow \mathbb {R}$ definida por partes como $f(x)=0$ si $x\in \mathbb {Q}$, $f(x)=x$ si $x\in \mathbb {R} \setminus \mathbb {Q}$ (es decir, esta función a cada número irracional le asigna a él mismo, y le asigna el valor 0 a cada número racional) es discontinua en todos los valores excepto en el 0. No existe ni un sólo intervalo (que contenga más de un punto) en el que la función sea continua.

Espero haber solventado tu duda. Saludos.

--Wewe 23:16 27 oct, 2005 (CEST)

---

---

El punto c debe ser un punto del dominio. Si éste es, además, punto de acumulación del dominio, podemos caracterizar la continuidad en c mediante límites (no hace falta que la función esté definida en un intervalo (c-e,c+e) con e>0, basta con que c esté en el dominio y sea punto de acumulación del dominio para caracterizar la continuidad en él por límites. Si el punto c del dominio no es punto de acumulación (se trata de un punto aislado del dominio), entonces f es continua en él pues cumpli trivialmente la definición: Si $\xi >0$ es tal que $(c-\xi ,c+\xi )\cap \operatorname {Dom} (f)=\{c\}$, dado cualquier $\varepsilon >0$, tomamos $0<\delta <\xi$ y tenemos que si $x\in \operatorname {Dom} (f)$ es tal que $|x-c|<\delta$, entonces tiene que ser $x=c$ y, por tanto, $|f(x)-f(c)|=|f(c)-f(c)|=0<\varepsilon$.

---

Con respecto a esa definición, yo no estoy de acuerdo que sea la de los límites. Creo que debería ser la siguiente:

f es continua, si para todo punto c en el dominio de f, si Xn es una sucesión contenida en el dominio de f, tal que Xn converge a c, entonces f(Xn) converge a f(c).

Tal vez la definición por límites sirva para un curso de cálculo que se trabaja con funciones muy elementales, pero por ejemplo, con la definicón por límites, si tenemos una función

f:{2}-->{2}, definida así f(x)=2. Esa es una fución continua, pero por límites. ¿como hacemos para estudiar el comportamiento de la función alrededor de 2?

Anthonny 15:59 13 may, 2007

funcion real de variable real

alguien me podria decir como afectan las funciones a nuestra vida diaria? muchas gracias.

---

Uff. Buena pregunta. Vamos a ver. Aparte de aquellas cosas que en el fondo son funciones pero que conscientemente nadie las trata como tales (ordenar los lápices en un estuche es una permutación, que es un tipo de función, pero a nadie se le ocurre tratar eso como una función), existe una multitud de ejemplos de funciones aplicadas a la vida diaria, sin las cuales las cosas serían realmente distintas.

Por poner tan sólo algunos ejemplos:

1. Transmisiones de comunicaciones mediante ondas electromagnéticas: como por ejemplo la radio, la televisión, la telefonía móvil... Una onda es uno de los ejemplos más patentes de función. Para poder extraer información de una onda se la trata como una función y se opera dicha función (existen distintas operaciones, como la transformada de Fourier, la de Laplace, etc.).

1. Las colas de un supermercado: seguro que todos nos preguntamos cómo se las arreglan las cajeras de los supermercados para dejar vacías las cajas justo cuando hay cola. ¿Por qué no están en su puesto de trabajo? Es más, ¿por qué no las despiden si faltan a su puesto de trabajo justo en esos momentos cuando se acumula la gente en la caja y la cola avanza tan lentamente? Pues resulta que no es ni mucho menos negligencia de las cajeras, sino que cumplen escrupulosamente los horarios que se les imponen. Esos horarios los establecen unas personas que han hecho un estudio estadístico referente a los horarios de compra de la gente, del tiempo que una persona está dispuesta a esperar en una cola antes de decidir dejar allí mismo la compra y volver a casa con las manos vacías, etc. ¿Para qué? Pues para no tener que estar pagando a una cajera para que esté sentada sin hacer nada en los horarios en los que no aparecen clientes, o no son suficientes como para necesitar más de una cajera. Se trata de minimizar los gastos, y estas cuestiones se estudian y solucionan usando funciones.

1. En general, el presupuesto de cualquier empresa de cierto tamaño, los gastos de producción, costes de material, cálculo de beneficios, cálculo del precio máximo al que pueden colocar un cierto producto, etc, se realiza siguiendo un patrón similar al anterior, es decir, calculando máximos y mínimos de funciones.

1. El rumbo de un barco (que transporte por ejemplo petroleo, u ordenadores), de un avión, la trayectoria de un satélite de telecomunicaciones, todas estas cuestiones se deciden usando funciones.

1. Predicción del tiempo meteorológico. Saber la temperatura y la humedad de un lugar a partir de las condiciones que presenta ese lugar en un instante dado, y llegar a determinar la probabilidad de que se produzcan precipitaciones, todo ello se realiza haciendo cálculos con funciones.

• La popularidad de un mandatario es función de su aciertos, la atenciòn que se recibe es producto del comportamiento de cada quien. "Siembra vientos cosecharàs tempestades".

Y podría seguir dando ejemplos concretos como para llnar una enciclopedia. Casi cualquier campo de la actividad humana que implique una cierta organización y predicción de los acontecimientos futuros de cierta envergadura se realiza mediante cálculo de funciones. El precio que pagas por cualquier cosa, la cantidad de medicamento que hay en una pastilla, el sueldo que cobras, el voltage que puede circular por un aparato eléctrico... Sin hablar ya de los cálculos necesarios para construir un edificio, un puente, un automovil o símplemente una bicicleta.

Espero que te sirva para aclarater un poco. Saludos.

--Wewe 21:14, 8 noviembre 2005 (CET)

Edición de las 16:35 del 24 de Enero del 2007.

Hola:

He revertido los cambios que se hicieron en esa edición. Quise ponerme en contacto con el autor de los cambios para avisarlo, pero lo hizo entrando sin cuenta registrada, pues sólo aparece la dirección I.P.

La razón de revertir los cambios es que el resultado final no se comprendía. Había hecho algunos cambios y creo que pude interpretar qué quería decir, pero el texto en sí había quedado incomprensible (entre otras cosas no había apretado el botón de "Fórmula matemática (LaTeX)" para editar el símbolo \mathbb{R}, con lo que aparecía los siguiente "Así pues, una función f continua \mathbb{R} [...]" en lugar de "Así pues, una función f continua $\mathbb {R}$ [...]", cosa que, por otro lado, no tiene sentido).

De paso he hecho un pequeño cambio de ubicación de cierta gráfica, creo que ahora se comprende mejor que lo que se dibuja (y de lo que habla el texto adyacente) es una función no continua en cierto punto (que es lo que he creído entender que el autor de los cambios anteriores pretendía poner de manifiesto).

Espero que el autor de los cambios sea comprensivo y comprenda que le haya revertido. Por supuesto (no hace falta que lo diga) puede realizar los cambios que crea conveniente. Sólo le pediría que compruebe al finalizar el resultado.

Un saludo: --Wewe 19:57 27 ene 2007 (CET).

Error en el concepto

Hi! Soy nuevo en lo de editar o escribir artículos en Wikipedia. El otro día navegando leí de este articulo un concepto que esta mal. Es sobre si la función 1/x es continua o no. En efecto es continua, ya que solo tiene sentido evaluar la continuidad de una función sobre su dominio y no donde no esta definida (al caso en x=0). De manera similar sucedía en los dos siguientes casos. Note también que en la versión en inglés este error no aparecía, es más, mi corrección la base en su texto.

Recién veo q volvieron a poner la versión anterior con el error incluido. No es mi intención amedrentar al escritor ni nada por el estilo, lo único que voy hacer al tratar de volver a poner la versión corregida es evitar confusiones sobre el tema para los que lean el articulo.

Saludo.

Continuidad de una función en un punto

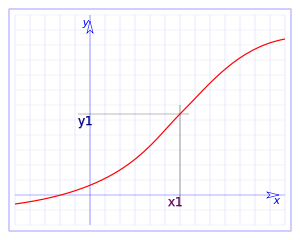
En el caso de aplicaciones de $\mathbb {R}$ en $\mathbb {R}$, y de una manera más rigurosa se dice que una función; f es continua en un punto x1 si existe f(x1), si existe el límite de f(x) cuando x tiende hacia x1 por la derecha, si existe el límite de f(x) cuando x tiende hacia x1 por la izquierda, y además coinciden con f(x1).

Así pues, una función f continua en el punto x1 implica lo siguiente:

• Existe f(x1):

$\exists f(x1)$

• tiene limite por la izquierda:

$\exists \lim _{x\to x1^{-}}f(x)\in \mathbb {R}$

• tiene limite por la derecha:

$\exists \lim _{x\to x1^{+}}f(x)\in \mathbb {R}$

• El límite por la derecha por la izquierda y el valor de la función coinciden:

$\lim _{x\to x1^{-}}f(x)=\lim _{x\to x1^{+}}f(x)=f(x1)$

Si la función no Existe f(x1) en un punto, la función es discontinua en ese punto, igual que la función raid es discontinua para x= 0. Es la definición de continuidad de funciones en cualquier texto de matemáticas. HiTe 13:47 29 jul 2007 (CEST)

La continuidad es una propiedad

Esta bien tu definición de límite, es más si te fijas con tu definición en ningún momento contradice q 1/x no sea continua, ya q en todo su dominio las 3 condiciones se cumple.

Ahora, uno no puede evaluar fuera del dominio por un simple hecho, no es función en esos puntos!!. La continuidad es una propiedad de las funciones, o sea, se evalua sobre funciones. Para algo ser una función su dominio debe estar bien definido. Es como decir que la función logaritmica es discontinua en -1 (sobre R), cuando nisiquiera existe para valores negativos (y el cero).

En los cursos de análisis siempre se da este ejemplo como función discontinua, pero amplian el dominio definiendolo con algún valor arbitrario. Pero pocas veces se menciona que si no estuviera definida para x = 0, la función es continua.

Repito, para f(x)=1/x con x en R-{0}, para todos los valores de x, f(x) cumple con las condiciones de continuidad. Tu definicion es correcta, el problema que estas aplicando cosas que no estan en la misma para determinar la discontinuidad.

La continuidad es una propiedad

Se entiende que una función es continua en R, si definimos un dominio restringido todas las funciones son continuas, la función parte entera también es continua en cada uno de los intervalos... [-1,0), [0,1), [1,2), ...

La funciones definidas para distintos intervalos de x, puede ser discontinua en los puntos de cambio de intervalo, como por ejemplo:

• La Función parte entera de x, E(x), donde E(x) es el mayor número entero inferior o igual a x, tal que:

E(x) ≤ x < E(x) + 1.

Su curva es una sucesión de segmentos horizontales a distintas alturas. Esta función no es continua en los enteros, pues los límites a la izquierda y a la derecha difieren de uno, pero es continua en los segmentos abiertos (n, n+1) donde es constante.

una cosa es determinar si una función es continua y cuales son sus puntos de discontinuida y de que tipo de discontinuidad se trata, y otra definir un entorno restringido, eliminando los puntos de discontinuidad, donde esta función es continua, si eliminas algún punto de la función, para que esta sea continua, estas reconociendo que la función es discontinua en ese punto.

según esto la función:

$f(x)={\frac {x^{2}-4}{x-2}}$

Seria continua en un entorno distinto de 2.

Presenta los siguientes limites por la izquierda y por la derecha:

$\lim _{x\to 2^{-}}{\frac {x^{2}-4}{x-2}}=4$

$\lim _{x\to 2^{+}}{\frac {x^{2}-4}{x-2}}=4$

pero la función para x= 2 no esta definida:

$f(2)={\frac {x^{2}-4}{x-2}}={\frac {0}{0}}$

HiTe 14:31 30 jul 2007 (CEST)

La continuidad es una propiedad...

En realidad no a todas las funciones se les puede restringir el dominio para hacerlas continuas. Un ejemplo es la funcion f(x):{ 0 si x es racional y 1 si x es irracional }. Esta función es discontinua para cualquier punto del dominio. La funcion x^2-4/(x-2) tb es continua. Uno no restringe el dominio en ningun momento, simplemente uno no puedo definirlo para todos los Reales. si x = 2, la función no representa valor alguno. Como no esta definida en ese punto, esto no afecta a la continuidad o discontinuidad de la misma. Distinto sería si se "ampliara el dominio" y se define algun valor cuando x = 2. Ahí sería discontinua si f(2) <> 4. El eje fundamental de la cuestión sobre si 1/x para R-{0} es o no continua, no es si cumple o no las hipotesis de continuidad, sino q para x = 0 no cumple las hipotesis de función! Y al no ser función en ese punto no se pueden evaluar las hipotesis de continuidad. En gral. recien hoy leo bien el articulo de continuidad y quizás habría q hacer algunas salvedades en algunos ejemplos en lo q respecta al dominio para evitar confusiones, pero eso sería despues q quede claro este mini-debate, sino no tiene sentido (Tambien creo q estaría bueno inspirarse en algunos de los conceptos del articulo en inglés)

Actualización: Acá encontre un articulo que habla exclusivamente sobre discontinuidad

1/x no es continua en x= 0

• Calculo diferencial e integral

Nikolaj Piskunov

Editorial Montaner y Simon SA

• Análisis matematico

R. Losada Rodrígez

Editorial: Pirámide

---

El trabajo de R. Losada Rodrígez no lo conozco. Si conozco el de Nikolai Piskunov, y trabaje en un curso con el vol 2 de Cal. Dif e Int. Me sorprende q diga algo así sin extender la función, recuerdo q es muy meticuloso y no dejaba muchos detalles librados al azar. Tengo q verlo con mis ojos. En estos días debería pasar por la facu, voy a tratar de buscarlo en la biblioteca, sin embargo por si las dudas, si tenes algun medio para digitalizar las páginas sería grandioso, y así poder ver el texto.

Aun así, esto no es solo ver las referencias q uno puede dar, sino que dicen esas referencias (y por eso quiero consultar yo mismo el libro). En los artículo en inglés muestran sus resultados de manera muy amena, eso es a veces mas válido q las cientos de miles de personas q evaluaron y correguieron los artículos hasta ser lo q son.

Partiendo de la definición de continuidad, uno construye la de discontinuidad. ¿Dondé esta el error en la definición que dan de discontinuidad en esta página?

A nivel lógico sería algo así: Si se niega la existencia de la función, uno no niega la tesis de continuidad, sino uno niega la hipotesis de continuidad, y por lo tanto no se puede determinar nada.

Hay que cambiar todas las x1 por $x_{1}$

Pues eso mero, creo que es mejor usar subíndices para evitar confusión, en la literatura prácticamente siempre usan subíndices.

Discontinuidad de segunda especie

En el ejemplo de discontinuidad de segunda especie $f(x)={\sqrt {x}}$ no es una función, es una relación, por tanto no puedes decir que presenta una discontinuidad, porque una discontinuidad se da es en funciones no en relaciones. Para que $f(x)={\sqrt {x}}$ sea función, debe restringirse su rango ya sea de $[0,\propto ]$ o de $[0,-\propto ]$. Sólo en ese caso podría considerarse función y por ende decir que presenta una discontinuidad de segunda especie.

Comentario

lo que se nota de todos los chavitos arriba es que les da miedo usar la definición $\varepsilon -\delta$ que es la que presenta menos ambigüedades y la que le da mucho miedo a los inges, jeje--kid 02:17 29 dic 2007 (CET)

Cambiar el inicio del artículo

Creo que debería cambiarse el inicio del artículo porque:

1. No hace referencia a qué se trata de un artículo de matemáticas.
2. No explica el concepto de continuidad sino que directamente da una de las muchas definiciones de función continua
3. La definición que da de continuidad es la definición dentro de espacios topológicos, pero dentro del artículo no se hace en ninguna referencia a espacios topológicos sino a la definición de funciones continuas de números reales. Debería darse una explicación general explicando que hay diversas definiciones de continuidad según dónde está definida la función y enlazar como en la página en inglés a otro artículo donde se desarrollase la definición y propiedades en los espacios topológicos.

—jjmf (discusión) 17:48 3 jul 2008 (UTC)

Estoy de acuerdo con que hay que mejorar el artículo. Sé valiente editando páginas. HUB (discusión) 16:57 4 jul 2008 (UTC)

¿Dibujable?

No estoy de acuerdo con incluir esta "definición" al inicio del artículo, ni tampoco en la sección "Funciones reales de una variable real":

"Intuitivamente una función continua es aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel."

Puesto que eso no es necesariamente cierto, por ejemplo, la siguiente función es continua y no se puede dibujar:

http://www.monografias.com/trabajos16/convergencia-uniforme/Image4465.gif

Tal vez sería bueno mencionar que sucede muy a menudo, pero tampoco se puede tomar como definición informal, para eso está mejor "para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función"

Mirando el artículo en inglés me doy cuenta que en el inicio del artículo advierten al menos 2 veces que no es correcto decir que las funciones continuas son las dibujables sin levantar el lapiz del papel, y en la sección de funciones reales de una variable real dice que las graficas continuas son aquellas que no tienen "agüjeros" o "saltos", y eso es mucho mas preciso que decir que son dibujables. --189.161.174.159 (discusión) 08:30 25 jun 2009 (UTC)

Para rato

Al definir la continuidad de una función, en un punto de su dominio, por el procedimiendo delta- épsilon se exige que el valor absoluto en el dominio basta que sea menor que delta, y no se compara con cero. Punto de vista de Courant y John en su clásico Introducción cálculo y análisis matemático. También se va a consultar Cálculo de Banach.Son dos "Everest" en este tema.--Julio grillo (discusión) 13:59 7 dic 2011 (UTC)

Habría que puntualizar mejor

Para empezar, llamar discreta a una función no continua no me parece una buena idea. De siempre se ha considerado que una función que no es continua globalmente es una función discontinua. Nunca he visto en ninguna parte documentación que acredite tal calificativo ni he conocido a nadie que use el término 'discreto' como equivalente de discontinua (ni me gustaría conocerlo). En todo caso tendría sentido decir que una función es discreta si está definida únicamente sobre puntos aislados, lo cual tiene más sentido y lógica con el significado de discreto.

Por otro lado, en ningún momento se hace referencia a que la continuidad es una propiedad local y eso si que me parece importante destacarlo en el artículo. Queda implícito en la caracterización por límites que hay hecha, pero habría que indicarlo explícitamente.

Tampoco comprendo porqué se pone en la parte de cálculo y derivabilidad "Sobre esto consultar Calculus de Spivak." Para eso está la sección de bibliografía y la de referencias.

Un saludo, --DavosMat (discusión) 11:17 16 sep 2013 (UTC)