Diagrama de Moody
El diagrama de Moody es la representación gráfica en escala doblemente logarítmica del factor de fricción en función del número de Reynolds y la rugosidad relativa de una tubería, diagrama hecho por Lewis Ferry Moody.
En la ecuación de Darcy-Weisbach aparece el término que representa el factor de fricción de Darcy, conocido también como coeficiente de fricción. El cálculo de este coeficiente no es inmediato y no existe una única fórmula para calcularlo en todas las situaciones posibles.
Se pueden distinguir dos situaciones diferentes, el caso en que el flujo sea laminar y el caso en que el flujo sea turbulento. En el caso de flujo laminar se usa una de las expresiones de la ecuación de Poiseuille; en el caso de flujo turbulento se puede usar la ecuación de Colebrook-White además de algunas otras cómo ecuación de Barr, ecuación de Miller, ecuación de Haaland.
En el caso de flujo laminar el factor de fricción depende únicamente del número de Reynolds. Para flujo turbulento, el factor de fricción depende tanto del número de Reynolds como de la rugosidad relativa de la tubería, por eso en este caso se representa mediante una familia de curvas, una para cada valor del parámetro , donde k es el valor de la rugosidad absoluta, es decir la longitud (habitualmente en milímetros) de la rugosidad directamente medible en la tubería.
En la siguiente imagen se puede observar el aspecto del diagrama de Moody.
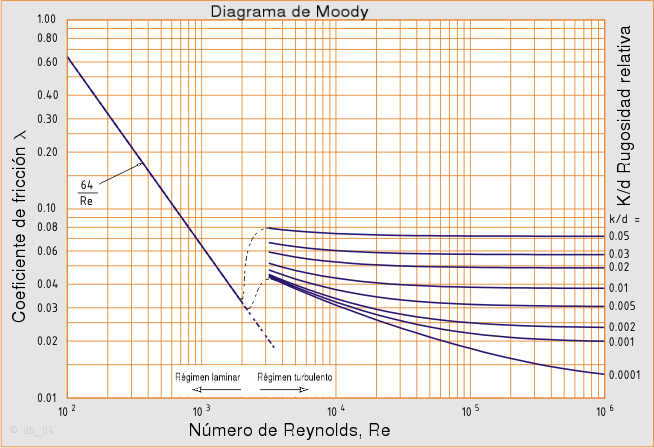
Expresión matemática[editar]
k/D = rugosidad relativa total
Re = Número de Reynolds
λ = factor de fricción
D = diámetro interno de la cañería
k/D = rugosidad relativa
Re = Número de Reynolds
λ = factor de fricción
k/D = rugosidad relativa
Re = Número de Reynolds
λ = factor de fricción
Véase también[editar]
Referencias[editar]
- Hidráulica de los canales abiertos. Ven Te Chow. 1982. ISBN 968-13-1327-5





