Cotangente

La cotangente, abreviado como cot, cta o cotg, es la razón trigonométrica inversa de la tangente, o también su inverso multiplicativo:
Forma geométrica[editar]

Si trazamos una recta horizontal que pase por F, corta a la recta r en G, con esto tenemos:

Otro planteamiento se hace trazando la recta perpendicular a r por B, que corta el eje y en K, con lo que tenemos:
Con lo que tenemos otra representación geométrica distinta de la anterior.
Representación gráfica[editar]

Tangente y cotangente de un ángulo[editar]
Partiendo de la definición de cotangente como la inversa de la tangente:
y conociendo la función tangente de un ángulo:
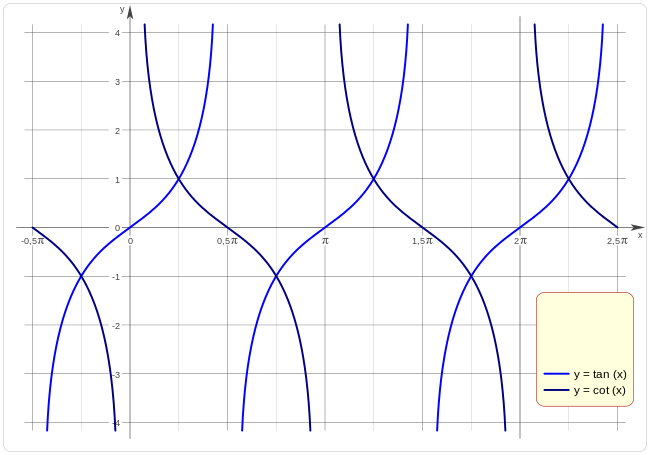
podemos ver que para los valores en los que la tangente vale cero, la cotangente se hace infinito, si la función tangente tiende a cero desde valores negativos la cotangente tiende a: .
mientras que cuando la tangente tiende a cero desde valores positivos la cotangente tiende a: .
Este razonamiento de la tangente sobre la cotangente es recíproco para los valores en los que la cotangente se hace cero. Es fácil de ver que cuando la tangente de un ángulo vale uno, la cotangente de ese mismo ángulo también vale uno.
Véase también[editar]
Referencias[editar]
Bibliografía[editar]
- Cobo Mérida, Purificación (9 de 2008). Trigonometría, 4 ESO. Materiales Didácticos Bemal. ISBN 978-84-612-6049-2.
- Cortés Espinosa de los Monteros, Nuria (2 de 2008). Actividades para unidad didáctica sobre trigonometría. Ediciones Didácticas y Pedagógicas S.L. ISBN 978-84-936336-3-9. «1 CD-ROM».
Enlaces externos[editar]
- Weisstein, Eric W. «Cotangente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Trigonometría
- Aula Virtual de Trigonometría
- Precálculo21, Trigonometría
- Matemática - Trigonometría










