Coeficiente de Poisson

El coeficiente de Poisson (denotado mediante la letra griega ) es una constante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento. El nombre de dicho coeficiente se le dio en honor al físico francés Simeon Poisson.
La mayoría de los materiales tienen valores de la relación de Poisson que oscilan entre 0,0 y 0,5. Para los materiales blandos,[1] como el caucho, donde el módulo aparente es mucho mayor que el módulo de cizallamiento, el coeficiente de Poisson es cercano a 0,5. Para las espumas de polímero de célula abierta, la relación de Poisson es cercana a cero, ya que las células tienden a colapsar en compresión. Muchos sólidos típicos tienen relaciones de Poisson del orden de 0,2-0,3.
Origen[editar]
El coeficiente de Poisson es una medida del efecto Poisson, el fenómeno por el cual un material tiende a expandirse en direcciones perpendiculares a la dirección de compresión. Por el contrario, si el material se estira en lugar de comprimirse, normalmente tiende a contraerse en las direcciones transversales a la dirección de estiramiento. Es frecuente observar que cuando se estira una goma elástica, ésta se vuelve notablemente más fina. De nuevo, la relación de Poisson será la relación entre la contracción relativa y la expansión relativa y tendrá el mismo valor que el anterior. En algunos casos poco frecuentes,[2] un material se encogerá realmente en la dirección transversal cuando se comprima (o se expandirá cuando se estire), lo que dará lugar a un valor negativo del coeficiente de Poisson.
El coeficiente de Poisson de un material estable, isotrópico, lineal elástico debe estar entre -1,0 y +0,5 debido al requisito de que el módulo de Young, el módulo de cizalladura y el módulo de compresibilidad tengan valores positivos.[3] La mayoría de los materiales tienen valores de la relación de Poisson que oscilan entre 0,0 y 0,5. Un material isótropo perfectamente incompresible deformado elásticamente a pequeñas deformaciones tendría una relación de Poisson de exactamente 0,5. La mayoría de los aceros y polímeros rígidos, cuando se utilizan dentro de sus límites de diseño (antes de fluencia), presentan valores de aproximadamente 0,3, que aumentan hasta 0,5 para la deformación posterior al rendimiento, que se produce en gran medida a volumen constante.[4] El caucho tiene una relación Poisson de casi 0,5. La relación de Poisson del corcho es cercana a 0, mostrando muy poca expansión lateral cuando se comprime, y la del vidrio está entre 0,18 y 0,30. Algunos materiales, como algunas espumas poliméricas, los pliegues de origami,[5][6] y ciertas células pueden presentar un coeficiente de Poisson negativo, y se denominan augéticos. Si estos materiales auxéticos se estiran en una dirección, se vuelven más gruesos en la dirección perpendicular. Por el contrario, algunos materiales anisótropos, como los nanotubos de carbono, los materiales de lámina plegada en zigzag,[7][8] y metamateriales auxéticos en forma de panal[9] por nombrar algunos, pueden presentar una o más relaciones de Poisson superiores a 0,5 en determinadas direcciones.
Suponiendo que el material es estirado o comprimido en una sola dirección (el eje x en el diagrama adjunto):
where
- es el coeficiente de Poisson resultante
- es la variación dimensional transversal
- es la variación dimensional axial
una variación dimensional positiva significa extensión mientras que una negativa significa contracción.
Relación de Poisson por cambios de geometría[editar]
Cambio de longitud[editar]

.
Para un cubo estirado en la dirección x (véase la figura 1) con un aumento de longitud de en la dirección x, y una disminución de longitud de en las direcciones y y z, las deformaciones diagonales infinitesimales vienen dadas por
Si la relación de Poisson es constante a través de la deformación, integrando estas expresiones y utilizando la definición de la relación de Poisson se obtiene
Resolviendo y exponenciando, la relación entre y es entonces
Para valores muy pequeños de y , se obtiene una aproximación de primer orden
Cambio volumétrico[editar]
Ahora se puede calcular el cambio relativo de volumen ΔV/V de un cubo debido al estiramiento del material. Usando y :
Utilizando la relación derivada anteriormente entre y :
y para valores muy pequeños de y , se obtiene la aproximación de primer orden:
Para materiales isótropos podemos utilizar relación de Lamé[10]
donde es el módulo de compresibilidad y es el módulo de Young.
Cambio de anchura[editar]
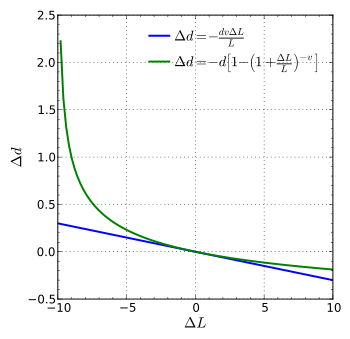
Si una varilla con diámetro (o anchura, o espesor) d y longitud L está sometida a tensión de forma que su longitud cambiará en ΔL entonces su diámetro d cambiará en:
La fórmula anterior sólo es válida en el caso de deformaciones pequeñas; si las deformaciones son grandes, puede utilizarse la siguiente fórmula (más precisa):
donde
- es el diámetro original
- es el cambio de diámetro de la varilla
- es la relación de Poisson
- es la longitud original, antes del estiramiento
- es el cambio de longitud.
El valor es negativo porque disminuye con el aumento de la longitud.
Materiales característicos[editar]
Materiales isótropos[editar]
Si se toma un prisma mecánico fabricado en el material cuyo coeficiente de Poisson pretendemos medir y se somete este prisma a una fuerza de tracción aplicada sobre sus bases superior e inferior, el coeficiente de Poisson se puede medir como: la razón entre el acortamiento de una longitud situada en un plano perpendicular a la dirección de la carga aplicada, dividido en el alargamiento longitudinal producido. Este valor coincide igualmente con el cociente de deformaciones, de hecho la fórmula usual para el coeficiente de Poisson es:
donde ε es la deformación.
Para un material isótropo elástico perfectamente incompresible, este es igual a 0,5. La mayor parte de los materiales prácticos en la ingeniería rondan entre 0,0 y 0,5, aunque existen algunos materiales compuestos llamados materiales augéticos que tienen coeficiente de Poisson negativo. Termodinámicamente puede probarse que todo material tiene coeficientes de Poisson en el intervalo (-1, 0,5), dado que la energía elástica de deformación (por unidad de volumen) para cualquier material isótropo alrededor del punto de equilibrio (estado natural) puede escribirse aproximadamente como:
La existencia de un mínimo relativo de la energía para ese estado de equilibrio requiere:
Esta última condición solo se puede cumplir si el coeficente de Poisson cumple .
Ley de Hooke generalizada[editar]
Conociendo lo anterior se puede concluir que al deformarse un material en una dirección producirá deformaciones sobre los demás ejes, lo que a su vez producirá esfuerzos en todos los ejes. Por lo que es posible generalizar la ley de Hooke como:
Es posible generalizar la Ley de Hooke (para fuerzas de compresión) en tres dimensiones:
onde:
- , , y son las deformaciones en la dirección de los ejes , y
- , , y son el stress en la dirección de los ejes , y
- es módulo de Young (el mismo en todas las direcciones: , , y para materiales isotrópicos)
- es la relación de Poisson (la misma en todas las direcciones: , y para materiales isotrópicos)
Materiales ortótropos[editar]
Para materiales ortotrópicos (como la madera), el cociente entre la deformación unitaria longitudinal y la deformación unitaria transversal depende de la dirección de estiramiento, puede comprobarse que para un material ortotrópico el coeficiente de Poisson aparente puede expresarse en función de los coeficientes de Poisson asociados a tres direcciones mutuamente perpendiculares. De hecho entre las doce constantes elásticas habituales que definen el comportamiento de un material elástico ortotrópico, solo nueve de ellas son independientes ya que deben cumplirse las restricciones entre los coeficientes de Poisson principales y los módulos de Young principales:
Entonces la ley de Hooke se puede expresar en forma matricial como:[11][12]
donde
- es el Módulo de Young a lo largo del eje
- es el Módulo de cizalladura en dirección en el plano cuya normal está en la dirección
- es la relación de Poisson que corresponde a una contracción en la dirección cuando se aplica una extensión en dirección .
Transversalmente isótropo[editar]
Los materiales transversalmente isótropos tienen un plano de isotropía en el que las propiedades elásticas son isótropas. Si suponemos que este plano de isotropía es , entonces la ley de Hooke toma la forma[13].
donde hemos utilizado el plano de isotropía para reducir el número de constantes, es decir, .
La simetría de los tensores de tensión y deformación implica que
Esto nos deja con seis constantes independientes . Sin embargo, la isotropía transversal da lugar a una restricción adicional entre y which is
Por lo tanto, hay cinco propiedades elásticas independientes del material, dos de las cuales son relaciones de Poisson. Para el supuesto plano de simetría, el mayor de y es la mayor relación de Poisson. Las otras relaciones de Poisson mayor y menor son iguales.
Valores para varios materiales[editar]
El coeficiente de Poisson es adimensional. Para ver el valor del coeficiente de Poisson para varios materiales consultar los valores del coeficiente de Poisson del Anexo:Constantes elásticas de diferentes materiales.
Materiales con coeficiente de Poisson negativo[editar]
Algunos materiales conocidos como augéticos presentan coeficientes de Poisson negativo. Cuando son sometidos a deformación positiva en sentido longitudinal, la deformación transversal también será positiva, es decir que aumentara el área de la sección. Para estos materiales, usualmente se debe a enlaces moleculares en orientación particular.[14]
Conversiones[editar]
| Fórmulas de conversión | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Los materiales elásticos lineales isótropos homogéneos tienen sus propiedades elásticas únicamente determinadas por dos módulos cualesquiera de los especificados anteriormente, por lo tanto, cualquier otro módulo de elasticidad puede ser calculado de acuerdo a estas fórmulas. | ||||||||||
Véase también[editar]
Referencias[editar]
- ↑ Para los materiales blandos, el módulo de masa (K) suele ser grande en comparación con el módulo de cizallamiento (G), de modo que pueden considerarse incompresibles, ya que es más fácil cambiar de forma que comprimir. Esto hace que el módulo de Young (E) sea y, por tanto, .Jastrzebski, D. (1959). Naturaleza y propiedades de los materiales de ingeniería (Wiley International edición). John Wiley & Sons, Inc.
- ↑ Lakes, R. y Wojciechowski, K.W., 2008. Compresibilidad negativa, relación de Poisson negativa y estabilidad. Physica Status Solidi B, 245(3), pp.545-551.
- ↑ Gercek, H. (January 2007). «Poisson's ratio values for rocks». International Journal of Rock Mechanics and Mining Sciences 44 (1): 1-13. doi:10.1016/j.ijrmms.2006.04.011.
- ↑ Park, RJT. Seismic Performance of Steel-Encased Concrete Piles
- ↑ Mark, Schenk (2011). Folded Shell Structures, PhD Thesis. University of Cambridge, Clare College.
- ↑ Wei, Z. Y.; Guo, Z. V.; Dudte, L.; Liang, H. Y.; Mahadevan, L. (21 de mayo de 2013). «Mecánica geométrica del origami plisado periódico». Physical Review Letters 110 (21): 215501. Bibcode:2013PhRvL.110u5501W. PMID 23745895. S2CID 9145953. arXiv:1211.6396. doi:10.1103/PhysRevLett.110.215501.
- ↑ Eidini, Maryam; Paulino, Glaucio H. (2015). «Desentrañando las propiedades metamateriales en láminas plegadas con base en zigzag». Science Advances 1 (8): e1500224. Bibcode:2015SciA....1E0224E. ISSN 2375-2548. PMC 4643767. PMID 26601253. arXiv:1502.05977. doi:10.1126/sciadv.1500224.
- ↑ Eidini, Maryam (2016). «Metamateriales mecánicos celulares de lámina plegada con base en zigzag». Extreme Mechanics Letters 6: 96-102. S2CID 118424595. arXiv:08104 1509. 08104. doi:10.1016/j.eml.2015.12.006.
- ↑ Mousanezhad, Davood; Babaee, Sahab; Ebrahimi, Hamid; Ghosh, Ranajay; Hamouda, Abdelmagid Salem; Bertoldi, Katia; Vaziri, Ashkan (2015- 12-16). «Metamateriales auxéticos jerárquicos en forma de panal». Scientific Reports 5: 18306. Bibcode:2015NatSR...518306M. ISSN 2045-2322. PMC 4680941. PMID 26670417. doi:10.1038/srep18306.
- ↑ Mott, P. H.; Roland, C. M. (3 de abril de 2012). «Límites de la relación de Poisson en materiales isótropos-resultado general para deformación arbitraria». Physica Scripta (División de Química, Laboratorio de Investigación Naval) 87 (5): 055404. S2CID 55920779. arXiv:1204.3859.
- ↑ Boresi, A. P, Schmidt, R. J. and Sidebottom, O. M., 1993, Advanced Mechanics of Materials, Wiley.
- ↑ Lekhnitskii, S. G. (1981). Theory of elasticity of an anisotropic elastic body. Mir Publishing. p. 36.
- ↑ Tan, S. C., 1994, Stress Concentrations in Laminated Composites, Technomic Publishing Company, Lancaster, PA.
- ↑ Lakes, Rod. «Negative Poisson's ratio». silver.neep.wisc.edu (en inglés estadounidense). Consultado el 4 de junio de 2018.
Bibliografía[editar]
- Ortiz Berrocal, L., Elasticidad, McGraw-Hill, 1998, ISBN 84-481-2046-9.
Enlaces externos[editar]
- (Inglés) Materiales Augéticos






























![{\displaystyle {\begin{cases}\varepsilon _{x}={\cfrac {1}{E}}\left[\sigma _{x}-\nu \left(\sigma _{y}+\sigma _{z}\right)\right]\\\varepsilon _{y}={\cfrac {1}{E}}\left[\sigma _{y}-\nu \left(\sigma _{x}+\sigma _{z}\right)\right]\\\varepsilon _{z}={\cfrac {1}{E}}\left[\sigma _{z}-\nu \left(\sigma _{x}+\sigma _{y}\right)\right]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeccd547e640d7f426408fe1dd085fe09f8c73cc)
![{\displaystyle \varepsilon _{xx}={\frac {1}{E}}\left[\sigma _{xx}-\nu \left(\sigma _{yy}+\sigma _{zz}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c2a4a45070b5bcb57f202d91db12bd6d3e7904d)
![{\displaystyle \varepsilon _{yy}={\frac {1}{E}}\left[\sigma _{yy}-\nu \left(\sigma _{xx}+\sigma _{zz}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d94d85b30fba005ed4c443b6a984061dbe5c2f9a)
![{\displaystyle \varepsilon _{zz}={\frac {1}{E}}\left[\sigma _{zz}-\nu \left(\sigma _{xx}+\sigma _{yy}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d07315b9cd2f3dc0b9014aad0b33dbf41fcb5ffa)






















































































