Código de Gauss

Un código de Gauss, del nombre del matemático Carl Friedrich Gauss es una lista de números que codifica una curva plana cerrada que presenta lazos. Ha sido extendido a la codificación de un nudo, e incluso de un enlace.

Histórico[editar]

En un artículo de 1823,^[1] Gauss se propone de demostrar que una curva planea cerrada de $N$ arrollamientos (número de vueltas sobre sí mismo efectuadas por un observador que recorre la curva) posee al menos $N-1$ lazos ( $N\geqslant 1$ ).

Con ocasión de esta demostración, introdujo el código que lleva su nombre, definido en el párrafo siguiente.

Como visualizado aquí, una curva circular con $n$ lazos tiene un índice de rotación igual a $N=n+1$ : posee el número mínimo de lazos de $N-1$ .

Definición[editar]

Por curva, se siente aquí una curva cerrada, teniendo una tangente en todos puntos, y cuyos puntos múltiples, en número finito, son todos dobles y transversos (tangentes no confundidas), que serán denominados aquí lazos. Eso equivale topológicamente a un grafo planar 4-regular (4 aristas que parten de cada vértice), los lazos correspondientes a las vértices del grafo (por grafo, se siente grafo no orientado y aceptando las aristas múltiples).

Dos curvas son equivalentes, si son imágenes mutuamente correspondidas por un homomorfismo del plan.

Habiendo numerado arbitrariamente de 1 a $n$ estos lazos, y habiendo escogido arbitrariamente un punto de salida sobre la curva, y un sentido de recorrido, el código de Gauss de la curva es entonces la lista de los $n$ números de los lazos que se obtienen sucesivamente cuando se efectúa un recorrido completo sobre la curva.

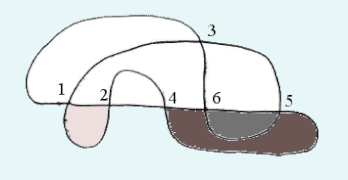
Encontrar en la figura que hay debajo los códigos de Gauss de las curvas que corresponden a las proyecciones de los nudo de trébol y nudo de ocho. Se puede señalar que ambas curvas de tienen el mismo código de Gauss, pero no son equivalentes en el plano (lo son en cambio sobre la esfera).

Un código de Gauss es siempre una lista de $2n$ números entre 1 y $n$ , cada uno repetido dos vez, que designaremos por palabra de Gauss.

Anotamos que el número de palabras de Gauss es el coeficiente multinomial ${\binom {2n}{2,2,...,2}}=(2n)!/2^{n}$ .

Curva a 7 lazos con su código y su diagramo de Gauss.
Códigos de Gauss de curvas a 3 o 4 lazos.
Los 3,5,15 curvas a respectivamente 3,4,5 lazos enumeradas por Nagy.

Diagrama de Gauss[editar]

Los diagramas de Gauss 1,1,3, y 5 realizables para n=1, 2,3, y 4 con curvas correspondientes ; para n = 4, los dibujos son hechos a mano alzada por Gauss.

Podemos visualizar un código de Gauss trazando un círculo, marcando los puntos sucesivos numerados por los números del código, y conectando por una cuerda los puntos igualmente numerados; el dibujo obtenido estando denominado diagrama de Gauss (o diagrama de cuerdas). El interés que está que con una rotación o una simetría, el diagrama ya no depende de la marcación de los lazos ni del sentido de recorrido.

Problema y condición de Gauss[editar]

Una palabra (o diagrama) de Gauss se dice realizable si proviene de una curva en el sentido anterior. Gauss se ha planteado el problema de caracterizar esta realizabilidad, y ha encontrado la condición necesaria siguiente :

En una palabra de Gauss realizable, dos números iguales están separados por un número par de números.

Por ejemplo, la palabra (1,2,1,3,3,2) no es realizable porque los 1 están separados por un solo número.

Para un diagrama de Gauss, la condición se traduce por el hecho que de parte y otra de una cuerda, hay un número par de puntos marcados.

Esta condición ha sido demostrada por Julius Nagy en 1927.^[2]

Breve demostración de este hecho.

Si los números entre dos números repetidos no tienen repetición, la porción de la curva correspondiente a las dos ocurrencias del mismo número forma una curva cerrada sin punto doble, o Curva de Jordan, separando el plano en dos partes relacionadas. Cuando la curva entra en la parte interna, necesariamente debe salir, de ahí el hecho de que el número de diferentes puntos de cruce del punto de partida sea par. En el caso de repeticiones anidadas, lo anterior se aplica a la mayoría de ellas, y después a las demás, sucesivamente.

Anotamos la utilización del teorema de Jordan en la demostración : sobre un toro por ejemplo, se puede encontrar una curva que tendría para código (1,2,1,2).

Desgraciadamente, Gauss había remarcado ya (^[1] página 284) que a partir de n = 5, esta condición de paridad no es suficiente ; por ejemplo la palabra (1,2,3,4,5,3,4,1,2,5) verifica la condición de paridad pero no se corresponde a ninguna curva a 5 lazos.

Varios matemáticos han dado y demostrado de las condiciones necesarias y suficientes de realizabilidad : Nagy en 1927,^[2] Dehn en 1936,^[3] Treybig en 1968,^[4] Marx en 1969,^[5] Bouchet en 1972,^[6] Lovasz en 1976,^[7] Rosenstiehl en 1976,^[8] Chaves y Weber en 1994,^[9] Burckel en 199?, y Grindblat-Lopatkin en 2017.

Rosenstiehl, por ejemplo, define el grafo de entrelazamiento G asociado a la palabra de Gauss, cuyos vértices son los números de 1 a n, dos números a y b conectados por una arista enlaces en la palabra : entre ambas ocurrencias de a, el número b aparece una vez y una sola (y pues entre ambas ocurrencias de b, a aparece una vez y una sola). Demuestra que la palabra de Gauss es realizable sí y sólo sí :

1) Las vértices de G son de grado par (condición de Gauss).

2) Si {a,b} no es una arista de G, las vértices a la vez conectadas a a y b están en números pares.

3) Las aristas {a,b} de G para las cuales las vértices a la vez conectadas a a y b están en números pares, forman el conjunto de las aristas incidentes a una misma vértice (o cociclo).

Reconstitución de una curva a marchar del código de Gauss.[editar]

Curva a 6 lazos de código de Gauss : (1,2,4,6,5,4,2,1,3,5,6,3)
Curva reconstituida a marchar del código de Gauss precedente.
Realización de la curva de código Gauss (1,2,1,2) sobre el tore.
Tentativa de reconstitución en el plan del código de Gauss (1,2,3,4,5,3,4,1,2,5) haciendo aparecer 3 lazos adicionales.
Realización de la curva de código Gauss (1,2,3,4,5,3,4,1,2,5) sobre el tore y el plan proyectivo.

Se trata de hecho de un problema similar a aquel de trazar un grafo planar conociendo las vértices y las aristas. Efectivamente, si el código de Gauss es $(x_{1},x_{2},...,x_{2n})$ , las 2n aristas del grafo asociado a la curva son las $\left\{x_{i-1},x_{i}\right\}$ , y las $\left\{x_{2n},x_{1}\right\}$ .

Por lo tanto, colocamos $n$ lazos que representan lazos numerados de 1 a $n$ , que conectamos por aristas que no deben cruzarse. La restricción es, cuando se llega a un lazo, partir sobre la misma rama del lazo. Esta restricción tiene entidad, porque por ejemplo la palabra (1,2,1,2) no es realizable, aunque hay un grafo planar que tenga como aristas {1,2},{2,1},{1,2} y {2,1} !

El website knotilus Archivado el 27 de junio de 2020 en Wayback Machine. posee una aplicación que permite reconstruir automáticamente la curva (o más bien, el nudo alternado) a partir del código de Gauss.

En el dibujo anterior, se ve una tentativa de reconstruir una curva asociada a la palabra (1,2,3,4,5,3,4,1,2,5) , lo que es imposible sin cruzarse en el plano. A derecha, realización de este mismo código sobre el toro y el plan proyectivo.

Notación de Dowker[editar]

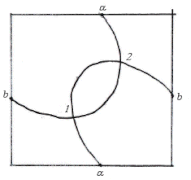
La notación de Dowker, constituye otra manera de codificar una curva : se ha escogido arbitrariamente un punto de salida sobre la curva y un sentido de recorrido, se numera sucesivamente los lazos por los números de 1 a 2 $n$ ; cada lazo recibe pues un par de números entre 1 y 2 $n$ , y la propiedad de paridad de Gauss indica que cada par está formada por un número par y de un número impar. La notación de Dowker es entonces la lista de los números pares asociados al número impares 1, 3, ..., $2n-1$ , en este orden. Por ejemplo los lazos de la curva dibujada, reciben los pares sucesivos {1,2},{3,6},{4,7}, y {5,8} ; la lista de los impares (1,3,5,7) está así asociada a la lista de las pares (2,6,8,4) que constituye una notación de Dowker de la curva.

Recuperamos un código de Gauss de la curva poniendo dos 1 en los lugares 1 y 2, dos 2 en los lugares 3 y 6, dos 3 en los lugares 5 y 8, y dos 4 a los lugares 7 y 4 : (1,1,2,3,4,2,3,4).

Anotemos que Gauss había introducido ya esta notación, numerando de 0 a 2n-1 en lugar de 1 a n ( página 284).

Para una curva a n lazos dados, hay a lo sumo 4n notaciones de Dowker posibles (debidas a los 2n puntos de salida y a los dos sentidos de recorridos), eventualmente confundidas. La notación que tiene el orden lexicográfico mínimo es la estándar.

Notaciones de Dowker estándares de las curvas asociadas a los cuatro primeros nudos primos.

Extensión a las nudos y enlaces.[editar]

Un diagrama de un nudo es una proyección planea del nudo que ha las propiedades de las curvas definidas anteriormente, con supe la indicación del pasaje encima, o debajo. El código de Gauss del nudo (o más bien de su diagrama) es entonces el código de Gauss de esta curva, los números que están afectados del signo más en caso de pasaje por encima, y del signo menos en caso de pasaje por debajo. El código de Gauss está pues formado de los 2 $n$ números de 1 a $n$ y de $-n$ a $-1$ . Para un enlace, se efectúa esto para cada hebra; pero hay que considerar que para cada hebra, los lazos intervienen con los demás hebras !

Señalamos que la condición de paridad de Gauss permite justificar que toda curva es el diagrama de un nudo denomina "alternado" (donde los pasajes encima y debajo se siguen de modo alternado) : si en un cruce dado se tiene un "puente", cuando se volverá a este mismo cruce, se tendrá obligatoriamente un "subterráneo". En cambio, hay nudos que no tienen ninguna proyección alternada, como por ejemplo el nudo primo 8.19.

Véase también[editar]

Referencias[editar]

↑ ^a ^b Carl Friedrich GAUSS (1900). Teubner, ed. Werke,VIII,1823 et 1844 (en alemán). Leipzig. p. 272 y 284.
↑ ^a ^b Julius V. Sz. NAGY (1927). «Uber ein toplogisches Problem von Gauss». Mathematische Zeitschrift, 26.
↑ DEHN, Max (1936). «Über kombinatorische Topologie, « », , , p.». Acta mathematica, 67, p. 123-168.
↑ L. B. TREYBIG (1968). «A characterization of the double point structure of the projection of a polygonal knot in regular position». Transactions of the American Mathematical Society, 130. p. 223-247.
↑ MARX, Morris L. (1969). «The Gauss realizability problem». Proceedings of the American Mathematical Society, 22. p. 610-613.
↑ André BOUCHET (1972). «Caractérisation des symboles croisés de genre nul». Comptes rendus de l'Académie des Sciences. p. 724.
↑ LOVASZ, Laszlo (1976). «A forbidden substructure characterization of Gauss codes». Bull. Amer. Math. Soc. , 82, n°1. p. 121-122.
↑ ROSENSTIEHL, Pierre (11 / 10 /1976). «Solution algébrique du problème de Gauss sur la permutation des points d'intersection d'une ou plusieurs courbes fermées du plan». Compte-rendus de l'Académie de Sciences, tome 283,. p. 551,553.
↑ Nathalie CHAVES y Claude WEBER (1994). «Plombages de rubans et problème des mots de Gauss». Expositiones Mathematicae,. p. 53-77.

Enlaces externos[editar]

Cursos sobre el asunto por Jeff Erickson Archivado el 12 de enero de 2018 en Wayback Machine..

Datos: Q96755115

[:2-1] Carl Friedrich GAUSS (1900). Teubner, ed. Werke,VIII,1823 et 1844 (en alemán). Leipzig. p. 272 y 284.

[:0-2] Julius V. Sz. NAGY (1927). «Uber ein toplogisches Problem von Gauss». Mathematische Zeitschrift, 26.

[3] DEHN, Max (1936). «Über kombinatorische Topologie, « », , , p.». Acta mathematica, 67, p. 123-168.

[4] L. B. TREYBIG (1968). «A characterization of the double point structure of the projection of a polygonal knot in regular position». Transactions of the American Mathematical Society, 130. p. 223-247.

[5] MARX, Morris L. (1969). «The Gauss realizability problem». Proceedings of the American Mathematical Society, 22. p. 610-613.

[6] André BOUCHET (1972). «Caractérisation des symboles croisés de genre nul». Comptes rendus de l'Académie des Sciences. p. 724.

[7] LOVASZ, Laszlo (1976). «A forbidden substructure characterization of Gauss codes». Bull. Amer. Math. Soc. , 82, n°1. p. 121-122.

[8] ROSENSTIEHL, Pierre (11 / 10 /1976). «Solution algébrique du problème de Gauss sur la permutation des points d'intersection d'une ou plusieurs courbes fermées du plan». Compte-rendus de l'Académie de Sciences, tome 283,. p. 551,553.

[9] Nathalie CHAVES y Claude WEBER (1994). «Plombages de rubans et problème des mots de Gauss». Expositiones Mathematicae,. p. 53-77.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]