Análisis de balance de flujo
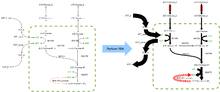
El análisis de balance de flujo (ABF) es un método matemático para analizar el metabolismo en un sistema biológico. A diferencia de otros métodos de modelaje, no requiere conocer previamente las concentraciones de los metabolitos o los detalles de la cinética enzimática del sistema. Se asume que el sistema bajo estudio se encuentra en estado estacionario. La técnica entonces intenta responder a la pregunta: dados algunos nutrientes conocidos, ¿cuál es el conjunto de flujos metabólicos que maximizan la tasa de crecimiento de un organismo preservando la concentración interna de metabolitos?
Un ejemplo notable del éxito del ABF es la capacidad de predecir con precisión la tasa de crecimiento del procarionte E. coli al ser cultivado en diferentes condiciones.[1] Los organismos apropiados para este análisis pueden ser cultivados en concentraciones de nutrientes definidas, midiendo sus tasas de crecimiento. Estas tasas de crecimiento experimentales son comparadas con las predicciones del ABF, lo que permite corregir el modelo con las observaciones.
Una buena descripción de los conceptos básicos de ABF se encuentra en el material suplementario de Edwards et al. 2001[1] (texto en inglés) el cual puede consultarse en el sitio web de Nature.[2] Otros recursos son el libro "Systems Biology" de B. Palsson,[3] y artículos por J. Orth,[4] por Lee et al. 2006[5] y Feist et al. 2008.[6]
Preparación del Modelo[editar]
Una guía para crear, preparar y analizar un modelo metabólico utilizando ABF, entre otras técnicas, fue publicada por Thiele y Palsson en 2010.[7] Las partes clave de la preparación del modelo son: anotar la red metabólica del sistema sin huecos, añadir restricciones al modelo y finalmente añadir una función objetivo (también llamada Función de Biomasa), para simular el crecimietno del organismo a modelar.
La Red Metabólica[editar]

Las redes metabólicas pueden variar en alcance, describiendo el metabolismo en sólo una ruta metabólica, una única célula, un tejido o un organismo. El único requisito para ser usada en ABF es que la red no contenga huecos. Esto usualmente implica una curación manual, es decir, la revisión de artículos científicos por humanos para extraer las reacciones metabólicas reportadas en el sistema. La curación puede tomar meses o incluso años. Algunos programas computacionales (Simpheny,[8][9] CellDesigner[10] y MetNetMaker[11]) aceleran la anotación de nuevas redes listas para su uso en ABF.
Generalmente los modelos son creados en formato BioPAX o SBML de modo que se pueda llevar a cabo un análisis o visualización más profundo; sin embargo estos formatos no son un requisito de ABF.
Restricciones[editar]
Un punto clave del Análisis de Balance de Flujos es la habilidad de añadir restricciones a las tasas de flujo de las reacciones en las redes, forzándolas a mantenerse dentro de un rango de valores seleccionados. Esto le permite al modelo simular con mayor precisión el metabolismo real. Las restricciones pueden dividirse en dos grupos: aquellas que regulan la ingesta y excreción de metabolitos, y aquellas que limitan el flujo a través de las reacciones metabólicas en el sistema. Los modelos metabólicos adaptados para ABF pueden ser analizados con COBRA toolbox[12] o FAME.[13]
Medio de Crecimiento[editar]
Los sistemas metabólicos requieren cierta entrada de nutrientes. Típicamente la tasa de obtención de nutrientes está regida por su diponibilidad en el medio (un nutriente que se encuentra ausente en el exterior no puede ser absorbido), su concentración y sus constantes de difusión (altas concentraciones de metabolitos con difusión rápida se absorben con mayor velocidad) y el método de absorción (marcando una diferencia entre transporte activo, difusión facilitada y difusión simple).
Si la tasa de absorción (o excreción) de ciertos nutrientes puede ser experimentalmente medida, la información puede añadirse como restricción a la tasa de flujo en los extremos del modelo metabólico. Esto garantiza que los nutrientes que no estén presentes o que no pueden ser ingeridos por el sistema no entren en su metabolismo (la tasa de flujo se restringe a cero), y que la simulación respete las tasas de absorción. Se provee así de un método secundario de asegurar que el metabolismo simulado contenga propiedades experimentalmente verificadas, que son algunas de todas las matemáticamente aceptables. En términos matemáticos, la aplicación de restricciones reduce el espacio de soluciones del problema en estado estacionario.
Restricciones internas[editar]
Además de las restricciones aplicadas en los extremos de la red metabólica, se pueden constriñir las reacciones de la sección interna de la red. Estas restricciones son usualmente sencillas; pueden dirigir una reacción en sólo un sentido debido a consideraciones energéticas o pueden fijar un límite máximo en la velocidad de una reacción debido a la velocidad finita de todas las reacciones en la naturaleza.
Función Objetivo[editar]
En ABF existe un gran número de soluciones matemáticamente aceptables para el problema del estado estacionario . Sin embargo algunas soluciones no tienen sentido biológico (no reflejan procesos que ocurran en la biología del sistema en la realidad), y las soluciones de interés son sólo aquellas que producen los metabolitos deseados en las proporciones correctas. El conjunto de metabolitos en proporciones correctas que el modelo de ABF intenta generar es llamado la función objetivo. Cuando se modela un organismo, la función objetivo es generalmente la biomasa del organismo y simula el crecimiento y la reproducción. La función de biomasa juega un papel muy importante en hacer los resultados del ABF aplicables biológicamente (al asegurar que la proporción de metabolitos producida por el metabolismo sea la correcta, por ejemplo) por lo que debe ser definida con sensibilidad o medida experimentalmente.
Al modelar redes más pequeñas la función objetivo se modifica de acuerdo a estas. Un ejemplo sería, en el estudio del metabolismo de la glucosa, definir la función objetivo como cierta proporción de ATP y NADH para simular la producción de metabolitos de alta energía por la ruta.
Descripción Matemática[editar]
Una red metabólica se compone de nodos (metabolitos) conectados por aristas con dirección (reacciones), por lo que puede representarse como una matriz. Las propiedades de esta matriz son bien conocidas permitiendo analizar con computadoras problemas biológicos. Un sistema biológico real es extremadamente complejo. La medición de suficientes parámetros para definirlo es difícil e imprecisa, y hacer simulaciones puede consumir grandes cantidades de tiempo. El Análisis de Balance de Flujo simplifica la representación del sistema al requerir menos parámetros (tasas de cinética enzimática, concentraciones de compuestos y constantes de difusión entre otros), reduciendo considerablemente el tiempo computacional requerido para efectuar la simulación.
Un ejemplo sencillo[editar]

Las concentraciones de todos los metabolitos y los flujos a través de todas las reacciones en este sistema pueden ser representados por las siguientes tres ecuaciones diferenciales.
Resolver este sistema de ecuaciones diferenciales no es difícil, pero rápidamente se vuelve computacionalmente caro conforme el número de ecuaciones en el sistema crece. Existe un segundo obstáculo en la resolución del sistema: las tasas de reacción and dependen de factores generalmente determinados por la teoría cinética de Michaelis-Menten, incluyendo los parámetros cinéticos de las enzimas y las concentraciones de los metabolitos. Aislar enzimas y medir sus parámetros cinéticos es una labor difícil, como lo es medir las concentraciones internas y las constantes de difusión de los metabolitos dentro del organismo. Por ello el acercamiento de ecuaciones diferenciales sirve únicamente para modelar el metabolismo los organismos más estudiados (link to Heinemann E. Coli paper with all internal fluxes measured and Manchester yeast paper with internal fluxes measured).
El poder de la homeostasis[editar]
Gran parte del poder del ABF proviene de aplicar el principio de estado estacionario al problema. Asumiendo que las concentraciones de los metabolitos en un sistema biológico permaneces casi constantes en el tiempo podemos aplicar la condición homeostática de que las concentraciones de metabolitos no cambian en el tiempo:
Para el caso general:
Así el problema se simplifica a balancear los flujos en el sistema; de ahí al nombre de Análisis de Balance de Flujo.
Este conjunto de ecuaciones es más sencillo de resolver. Para el ejemplo la única solución es la solución nula .
La matriz estequiométrica[editar]

Las ecuaciones diferenciales pueden ser representadas usando matrices. La matriz estequiométrica de las ecuaciones de arriba es:
Las matrices estequiométricas se utilizan también en química, Análisis de Control Metabólico[14] y sistemas dinámicos,[15] y son usualmente denotadas por la letra (refiriéndose al número en relación con la estequiometría, S está comúnmente reservada para la entropía). En Análisis de Balance de Flujo se denotan por la letra . En este punto es útil definir un vector en el que cada componente representa la tasa (o flujo a través) de la reacción respectiva dentro de la matriz estequiométrica.
La multiplicación de esta matriz, , con , es completamente equivalente a las ecuaciones derivadas directamente del diagrama de reacciones:
Aplicando la condición homeostática:
En general podemos escribir:
con el representando el vector nulo:
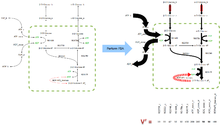
Esta operación en general se denomina obtener el Espacio nulo de la matriz . La operación es válida para todas las matrices. Dado que la matriz estequiométrica típica contiene más metabolitos que reacciones () y la mayoría de las reacciones son linearmente independientes existen muchos vectores que satisfacen la ecuación y abarcan el espacio nulo de .
Aplicación en la biología del sistema[editar]
El análisis del espacio nulo de matrices es común en álgebra lineal y muchos páquetes de software como Matlab y Octave pueden ayudar con el proceso. Sin embargo, conocer el espacio nulo de sólo nos dice todas las posibles colecciones de vectores de flujo (o combinaciones lineales de ellos) que balancean los flujos con la red metabólica. ABF tiene dos objetivos más: representar con precisión los límites del sistema y regresar la distribución de flujo más cercana a la que ocurre naturalmente dentro del sistema modelado.
Restricciones[editar]
La matriz estequiométrica está casi siempre indeterminada, es decir, el espacio de soluciones de es muy grande. El tamaño del espacio de soluciones puede reducirse y reflejar mejor la biología del problema mediante la aplicación de restricciones sobre las soluciones.
Restricciones termodinámicas[editar]
En principio todas las reacciones son reversibles. Sin embargo en los sistemas vivos muchas reacciones ocurren en una sola dirección. Esto puede deberse a la alta concentración de los reactivos comparados con los productos de la reacción, y más frecuentemente a la mucho menor energía libre de los productos comparados con los reactivos, lo que favorece masivamente la dirección directa de la reacción. Para reacciones ideales:
Para algunas reacciones se puede aplicar una restricción direccional (en este caso sólo se da la reacción directa):
En la realidad el flujo a través de una reacción no es infinito, dado que la cantidad de enzimas es finita, por lo que:
Medición de tasas de flujo[editar]
Algunas tasas de flujo pueden ser medidas experimentalmente () y los flujos dentro un modelo metabólico pueden ser constriñidos, dentro de cierto rango de error (), para asegurar que estos flujos conocidos sean reproducidos con precisión en la simulación.
La medición de flujos en los bordes de la red (en la ingesta y excreción de metabolitos) es sencilla, pero las mediciones en la región interna son más complejas y requieren técnicas que utilizan isótopos de metabolitos marcados radiactivamente o visibles en Resonancia magnética nuclear o Espectrometría de masa.
Optimización (la función objetivo)[editar]
Incluso después de la aplicación de restricciones existe un gran número de posibles soluciones al problema de balance de flujo. Si se define un objetivo de optimización, se puede utilizar programación lineal para encontrar una única solución óptima. El objetivo de optimización más común para la red metabólica de un organismo sería escoger el vector de flujo que maximiza el flujo a través de una función de biomasa, compuesta de los metabolitos constitutivos del organismo puestos en la matriz estequiométrica y denotada como o simplemente
En el caso más general cualquier reacción puede ser definida como una función de biomasa con la condición de ser maximizada o de ser minimizada si solo una solución óptima es deseada. Alternativamente y en el caso más general, se define un vector que contenga el conjunto de reacciones ponderadas que el modelo de programación lineal debe maximizar o minimizar:
En el caso en el que se tiene una sola función de biomasa/reacción separada, dentro de la matriz estequiométrica, se simplifica a un vector de ceros con un valor de 1 (o cualquier valor diferente de cero) en la posición correspondiente a esa función de biomasa. Cuando existen múltiples funciones objetivas separadas se simplifica a un vector de ceros con valores de ponderación en todas las funciones objetivo.
Simulación de perturbaciones[editar]


El Análisis de Balance de Flujo no es computacionalmetne intensivo, tomando tiempos en el orden de los segundos para calcularlos flujos óptimos para la producción de biomasa de un organismo sencillo (alrededor de 1000 reacciones). Esto significa que el efecto de eliminar reacciones de la red y/o cambiar las restricciones de flujo puede ser modelado con sensibilidad en una sola computadora.
Eliminación de una sola reacción[editar]
Es una técnica frecuentemente usada para buscar en una red metabólica las reacciones críticas para la producción de biomasa. Al remover cada reacción en una red por turnos y midiendo el flujo predicho para la función de biomasa, cada reacción puede clasificarse como esencial (si el flujo se ve sustancialmente reducido) o no esencial (si el flujo no cambia o se reduce ligeramente).
Inhibición de una reacción[editar]
La inhibición se simula restringiendo el flujo a través de una reacción. El efecto puede clasificarse como letal o no letal aplicando el mismo criterio que con eliminación, definiendo un punto de corte para distinguir entre “reducción sustancial” y “reducción ligera”. Generalmente la elección del punto de corte es arbitrria pero un estimado razonable puede obtenerse de experimentos de crecimiento sonde las inhibiciones o deleciones simuladas se llevan a cabo in vivo y la tasa de crecimiento es medida.
Interpretación de resultados[editar]
La utilidad de los análisis de eliminación e inhibición es más clara si existe una relación gen-proteína-reacción de la red estudiada con ABF. Entonces la información de qué reacciones son esenciales puede ser convertida a información de qué genes son esenciales (y por ende qué defectos génicos pueden causar una cierta enfermedad) o qué proteínas/enzimas son esenciales (y por ello los blancos más prometedores de antibióticos en patógenos).
Eliminación de reacciones en pareja[editar]
Una extensión de las eliminaciones sencillas son eliminaciones dobles donde todos los pares posibles de reacciones son eliminadas. Esto puede ser útil al buscar blancos de fármacos, pues permite simular tratamientos con múltiples blancos, tanto por un fármaco con más de un efecto o por combinaciones de fármacos.
Modificación del medio de crecimiento[editar]
ABF también ha sido utilizado para simular el cambio en la tasa de crecimiento dado por el medio de cultivo del sistema bajo estudio. Con E. coli las tasas de crecimiento predichas en diferentes medios mantienen una correlación con los resultados experimentales.[16] También se ha precisado el medio mínimo para cultivar Salmonella typhimurium.[17]
Comparación con otras técnicas[editar]
FBA provee de un análisis menos simplista que el Análisis del Punto de Asfixia (Choke Point Analysis), requiriendo mucha menos información de las tasas de reacción y una anotación de la red mucho menos completa que la requerida por una simulación dinámica completa. Al ocupar este nicho, ABF ha probado ser una técnica sumamente útil en el análisis de las capacidade metabólicas de sistemas celulares.
Análisis del punto de asfixia[editar]
A diferencia del Análisis del Punto de Asfixia, que sólo considera puntos en la red donde los metabolitos son producidos pero no consumidos y viceversa, ABF es una forma verdadera de modelaje de redes metabólicas puesto que sonsidera la red metabólica como una entidad completa en todas las etapas del análisis. Esto implica que los efectos a nivel red, como reacciones químicas en vías distantes afectándose mutuamente, pueden ser reproducidos en el modelo. La ventaja del Análisis del Punto de Asfixia consiste en que, por considerar cada reacción en aislamiento, puede sugerir cuáles son las reacciones importantes incluso si la red está altamente fragmentada y contiene huecos.
Simulación metabólica dinámica[editar]
A diferencia de simulación metabólica dinámica, ABF asume que la concentración interna de los metabolitos en un sistema se mantiene constante a lo largo del tiempo y por ello es incapaz de proveer otra cosa que soluciones del estado estacionario. Es improbable que ABF pueda simular el funcionamiento de una célula nerviosa. Debido a que la concentración interna de metabolitos no se considera en el modelo es posible que una solución de ABF contenga metabolitos a una concentración demasiado alta para ser biológicamente aceptable. Éste es un problema que se puede evitar con simulaciones metabólicas dinámicas.
Una ventaja de la simplicidad de ABF sobre las simulaciones dinámicas es que es por mucho computacionalmente más barato, permitiendo la simulación de muchas perturbaciones en la red. Una segunda ventaja es que el modelo reconstruido puede ser sustancialmente más sencillo, evitando la necesidad de considerar las tasas de interconversión de las enzimas y los efectos de interacciones complejas en la cinética enzimática.
Véase también[editar]
Referencias[editar]
- ↑ a b Edwards, J., Ibarra, R. & Palsson, B. In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data. Nature Biotechnology 19, 125–130(2001).
- ↑ http://www.nature.com/nbt/web_extras/supp_info/nbt0201_125/info_frame.html)
- ↑ Palsson, B.O. Systems Biology: Properties of Reconstructed Networks. 334(Cambridge University Press: 2006).
- ↑ Orth, J.D., Thiele, I. & Palsson, B.Ø. What is flux balance analysis? Nature Biotechnology 28, 245-248(2010).
- ↑ Lee, J.M., Gianchandani, E.P. & Papin, J.A. Flux balance analysis in the era of metabolomics. Briefings in bioinformatics 7, 140-50(2006).
- ↑ Feist, A.M. & Palsson, B.Ø. The growing scope of applications of genome-scale metabolic reconstructions using Escherichia coli. Nature biotechnology 26, 659-67(2008).
- ↑ Thiele, I. & Palsson, B.Ø. A protocol for generating a high-quality genome-scale metabolic reconstruction. Nature protocols 5, 93-121(2010).
- ↑ Schilling, C.H. et al. SimPheny: A Computational Infrastructure for Systems Biology. (2008).
- ↑ «Copia archivada». Archivado desde el original el 21 de abril de 2010. Consultado el 11 de marzo de 2010.
- ↑ http://www.celldesigner.org
- ↑ «Copia archivada». Archivado desde el original el 11 de junio de 2011. Consultado el 19 de abril de 2011.
- ↑ Becker, S.A. et al. Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox. Nature protocols 2, 727-38(2007).
- ↑ Boele J, Olivier BG, Teusink B. FAME: the Flux Analysis and Modeling Environment. BMC Syst Biol 6(1): 8. PMID 22289213, http://f-a-m-e.org/
- ↑ Reder, C (1988) Metabolic control theory: a structural approach. J Theor Biol. 135(2), 175-201. PMID 3267767
- ↑ Steuer, R and Junker, B H (2008) Computational Models of Metabolism: Stability and Regulation in Metabolic Networks in Advances in Chemical Physics, 142, 105-251
- ↑ Edwards, J., Ibarra, R. & Palsson, B. In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data. Nature Biotechnology 19, 125–130(2001).
- ↑ Raghunathan, A. et al. Constraint-based analysis of metabolic capacity of Salmonella typhimurium during host-pathogen interaction. BMC systems biology 3, 38(2009).


![{\displaystyle {d[A] \over dt}={d[C]_{1} \over dt}=v_{2}-v_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65b555a14119c68299687adfcd3c265904221782)
![{\displaystyle {d[C] \over dt}={d[C]_{2} \over dt}=v_{1}-v_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10b5f20d9bee0c3c95fd90492bb1644d958a0af9)
![{\displaystyle {d[B] \over dt}={d[C]_{3} \over dt}=-v_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afb97f31dec83fa0f568ce66d9b3c41a558cb35c)


![{\displaystyle {d[C]_{1} \over dt}={d[C]_{2} \over dt}={d[C]_{3} \over dt}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28ec18c2871b440e176d1437e385cf62bd07e3ee)
![{\displaystyle {d[C]_{i} \over dt}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c5bd4dfca5ec2d3ee93157cf1c6bfc3edc431f2)







![{\displaystyle {\begin{bmatrix}-1&1\\1&-1\\-1&0\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}-v_{1}+v_{2}\\v_{1}-v_{2}\\-v_{1}\end{bmatrix}}={\begin{bmatrix}{d[C]_{1} \over dt}\\[6pt]{d[C]_{2} \over dt}\\[6pt]{d[C]_{3} \over dt}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5416a35687e4274a0aa0c6b8e61c03d079863261)
![{\displaystyle {\begin{bmatrix}-1&1\\1&-1\\-1&0\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}-v_{1}+v_{2}\\v_{1}-v_{2}\\-v_{1}\end{bmatrix}}={\begin{bmatrix}{d[C]_{1} \over dt}\\[6pt]{d[C]_{2} \over dt}\\[6pt]{d[C]_{3} \over dt}\end{bmatrix}}={\begin{bmatrix}0\\0\\0\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a69330db14d692ecf23948d52de17a4ce2313ccd)
















