Algoritmo de Viterbi
El algoritmo de Viterbi es un algoritmo de programación dinámica que permite hallar la secuencia más probable de estados ocultos (el llamado camino de Viterbi) que produce una secuencia observada de sucesos, especialmente en el contexto de fuentes de información de Márkov y modelos ocultos de Márkov.
Se aplica de forma general en la descodificación de códigos convolucionales usados en redes de telefonía celular digital GSM y CDMA, módems de líneas conmutadas, satélites, comunicaciones espaciales y redes inalámbricas IEEE 802.11. También se usa en reconocimiento del habla, síntesis de habla, diarización, búsqueda de palabras clave, lingüística computacional y bioinformática.
Introducción[editar]
El algoritmo de Viterbi permite encontrar las secuencias de estados más probable en un Modelo oculto de Márkov (MOM), , a partir de una observación , es decir, obtiene la secuencia óptima que mejor explica la secuencia de observaciones.
Consideremos la variable que se define como:
es la probabilidad del mejor camino hasta el estado habiendo visto las primeras observaciones. Esta función se calcula para todos los estados e instantes de tiempo.
Puesto que el objetivo es obtener las secuencia de estados más probable, será necesario almacenar el argumento que hace máxima la ecuación anterior en cada instante de tiempo y para cada estado y para ello utilizamos la variable .
A continuación se detalla el proceso completo utilizando las funciones y .
Algoritmo[editar]
Inicialización[editar]
donde
Recursión[editar]
,
,
donde:
,
Terminación[editar]
Reconstrucción de la secuencia de estados más probable[editar]
,
donde:
Algunos de los cálculos del algoritmo de Viterbi recuerdan a los del algoritmo forward necesario para calcular eficientemente la probabilidad de una secuencia de observables. Una de las diferencias es la incorporación de la función (en lugar de sumar las probabilidades) para calcular la secuencia de estados más probable.
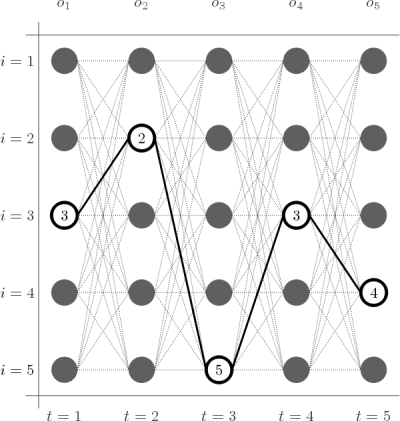
Ejemplo de secuencia de estados más probable
La figura muestra un ejemplo de secuencia de estados más probable en un Modelo Oculto de Márkov de 5 estados dada una secuencia de observaciones de longitud 5.
Aplicación del algoritmo de Viterbi[editar]
Muy usado para reconocimiento de voz, biología molecular, fonemas, palabras, codificadores entre otros. A cada secuencia de estados le corresponde una secuencia de etiquetas (o labels) de clasificación, es decir, palabras, caracteres, fonemas, sufijos. Dada una secuencia observada, se deduce la más probable secuencia de estados.
Desambiguación léxica categorial[editar]
Una de las aplicaciones del algoritmo de Viterbi es en el área de procesamiento del lenguaje natural, más concretamente en el proceso de desambiguación léxica categorial.
En este caso particular, los elementos de un Modelo Oculto de Márkov serían los siguientes:
- El conjunto de estados sería el conjunto de posibles etiquetas (categorías gramaticales) para las palabras.
- El conjunto de observables en cada uno de los estados corresponde con el conjunto de palabras distintas.
- El conjunto de probabilidades de transiciones entre estados sería la probabilidad de que una determinada categoría categorial siga a otra. Por ejemplo, la probabilidad de que la categoría nombre vaya detrás de la categoría determinante.
- El conjunto de probabilidades de las observaciones correspondería con la probabilidad de pertenencia de una palabra (un observable) a una determinada categoría. Por ejemplo, la probabilidad de que la palabra casa sea verbo, que será menor que la probabilidad de que esta misma palabra tenga la categoría gramatical nombre.
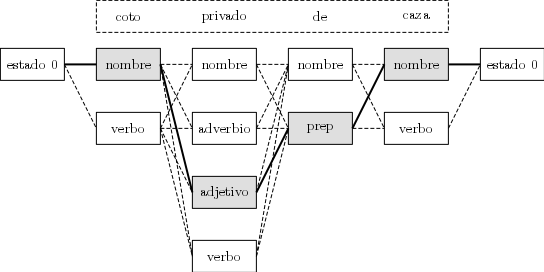
La figura siguiente muestra un ejemplo de etiquetado gramatical para la oración "Coto privado de caza"
En él, los observables son la secuencia de palabras de la oración. Se puede observar como para cada palabra se contempla sólo un conjunto limitado de posibles categorías gramaticales (caza puede ser o nombre o verbo). Este se debe a que la probabilidad de pertenencia de determinadas palabras a una categoría gramatical es nula (como la probabilidad de que la palabra caza sea adverbio). Esto simplifica enormemente los cálculos en el modelo.
Otras preguntas fundamentales[editar]
Otros dos problemas que es importante saber resolver para utilizar los MOM son:
- ¿Cuál es la probabilidad de una secuencia de observaciones dado un modelo ? Es decir, ¿cómo podemos calcular de forma eficiente ?. Para esto se puede usar el algoritmo de avance-retroceso.
- Dada una secuencia de observaciones , ¿cómo podemos estimar los parámetros del modelo para maximizar . En este caso el objetivo es encontrar el modelo que mejor explica la secuencia observada. Para esto se puede usar el algoritmo de Baum-Welch.
Véase también[editar]
Referencias[editar]
Enlaces externos[editar]
- Entrevista con Andrew Viterbi, que incluye información sobre el descubrimiento del algoritmo de Viterbi
- Implementación en Perl del algoritmo de Viterbi







![{\displaystyle \delta _{t+1}{(j)}={\biggl [}\max _{1\leq i\leq N}{\delta _{t}{(i)(a_{ij})}}{\biggr ]}b_{j}(o_{t+1})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93b2b8d6c56ebc247b475020a7d4b158b0429be5)






![{\displaystyle \delta _{t+1}{(j)}={\biggl [}\max _{1\leq i\leq N}{\delta _{t}{(i)}a_{ij}}{\biggr ]}b_{j}(o_{t+1})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca0926dbc65c8be0eefe97969b1d273cb433ea45)