Aguja de Buffon




La aguja de Buffon es un clásico problema de probabilidad geométrica, de realización práctica y cuyo interés radica en que es un método fácil para ir aproximando el valor del número π a partir de sucesivos intentos. Fue planteado por el naturalista francés Buffon en 1733 y reproducido por él mismo ya resuelto en 1777.[1]
Se trata de lanzar una aguja sobre un papel en el que se han trazado rectas paralelas distanciadas entre sí de manera uniforme. Se puede demostrar que si la distancia entre las rectas es igual a la longitud de la aguja, la probabilidad de que la aguja cruce alguna de las líneas es .
De esa manera:
siendo N el número total de intentos y A el número de veces que la aguja ha cruzado alguna línea.
Si la aguja es más corta que la distancia entre las rectas la probabilidad disminuye proporcionalmente al cociente entre la longitud de la aguja y la distancia entre las rectas, tomando el valor donde L es la longitud de la aguja y D la interdistancia entre las rectas.
En este caso:
La tercera situación, en que la longitud de la aguja es mayor que la distancia entre las rectas lleva a un resultado bastante más complicado.
Una generalización obvia de este problema es el problema de la Aguja de Buffon-Laplace, donde la aguja, en vez de lanzarse sobre un papel rayado, se lanza sobre una cuadrícula. Se llama de Buffon-Laplace pues aunque Buffon lo resolvió también en 1777, su solución contenía un error. Fue corregido por Laplace en 1812.
Solución[editar]
Planteamiento[editar]
El planteamiento matemático de este problema es:
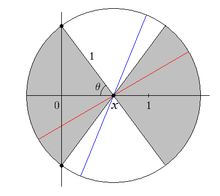
Sea una aguja de longitud lanzada sobre un plano segmentado por líneas paralelas separadas unidades (ver imagen). ¿Cuál es la probabilidad que la aguja cruce alguna línea?
Supuestos[editar]
Sea la distancia entre el centro de la aguja y la línea más cercana, , y sea el ángulo entre la aguja y las líneas, . También es importante hacer ver que esta solución es para el caso cuando (las agujas miden menos que la distancia entre las líneas).
Solución[editar]
La variable aleatoria se distribuye uniformemente (de forma continua) entre el 0 y , por lo que su función de densidad de probabilidad es:
Por su parte, la variable aleatoria , al igual que se distribuye uniformemente entre 0 y , por lo que su función de densidad de probabilidad es:
Al y ser variables aleatorias independientes, la función conjunta de densidad es simplemente el producto de ambas:
La condición para que una aguja cruce una línea es:
Ahora se busca la función de probabilidad de este problema, la cual se obtiene integrando para ambas variables la función de densidad, lo cual es:
Si se lanzan agujas y cruzan alguna línea, se tiene que:
De donde despejando , tenemos:
Referencias[editar]
- ↑ «La Aguja de Buffon». Consultado el 31 de enero de 2020.
Enlaces externos[editar]
- Simulación Java del problema de la aguja de Buffon
- Weisstein, Eric W. «El problema de Buffon resuelto matemáticamente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «El problema de Buffon-Laplace resuelto matemáticamente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Explicación para el caso l=t con applet Descartes simulando las tiradas de la aguja.








![{\displaystyle x\in [0,t/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3a971b44cd6f17c76dca585bd98c315f802ffe)

![{\displaystyle \theta \in [0,\pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab72704c8250f43c18cc3d08ef11ab93a0c28636)












