Diferencia entre revisiones de «Plano inclinado»

← Ir a diferencia anterior Ir a siguiente diferencia →

Contenido eliminado Contenido añadido

En renglón

Revisión del 13:07 2 feb 2022

Plano inclinado y las fuerzas que actúan sobre el sólido.

El plano inclinado es una máquina simple que consiste en una superficie plana que forma un ángulo agudo con el suelo y se utiliza para elevar cuerpos a cierta altura.^[1]

Tiene la ventaja de necesitarse una fuerza menor a la empleada para levantar dicho cuerpo verticalmente (logrado gracias a la descomposición de fuerzas), aunque se deba aumentar la distancia recorrida y vencer la fuerza de rozamiento.

Visión general

Las leyes que rigen el comportamiento de los cuerpos en un plano inclinado fueron enunciadas por primera vez por el matemático Simon Stevin, en la segunda mitad del siglo XVI.^[2]

Para analizar las fuerzas existentes sobre un cuerpo situado sobre un plano inclinado, hay que tener en cuenta la existencia de varios orígenes en ellas.

En primer lugar se debe considerar la existencia de una fuerza de gravedad, también conocida como peso, que es consecuencia de la masa (M) que posee el cuerpo apoyado en el plano inclinado y tiene una magnitud de M.g con una dirección vertical^[3] y representada en la figura por la letra G.
Existe además una fuerza normal (N), también conocida como la fuerza de reacción ejercida sobre el cuerpo por el plano como consecuencia de la tercera ley de Newton, se encuentra en una dirección perpendicular al plano^[3] y tiene una magnitud igual a la fuerza ejercida por el plano sobre el cuerpo. En la figura aparece representada por N y tiene la misma magnitud que F₂= M.g.cos α y sentido opuesto a la misma.
Existe finalmente una fuerza de rozamiento, también conocida como fuerza de fricción (F_R), que siempre se opone al sentido del movimiento del cuerpo respecto a la superficie,^[4] y cuya magnitud depende tanto del peso como de las características superficiales del plano inclinado y la superficie en contacto del cuerpo que proporcionan un coeficiente de rozamiento. Esta fuerza debe tener un valor igual a F₁=M.g.sen α, para que el cuerpo se mantenga en equilibrio. En el caso en que F₁ fuese mayor que la fuerza de rozamiento el cuerpo se deslizaría hacia abajo por el plano inclinado. Por tanto para subir el cuerpo se debe realizar una fuerza con una magnitud que iguale o supere la suma de F₁ + F_R.

Historia

Prueba de Stevin

En 1586, el ingeniero flamenco Simon Stevin (Stevinus) dedujo la ventaja mecánica del plano inclinado mediante un argumento que utilizaba un collar de cuentas.^[5] Imaginó dos planos inclinados de igual altura pero diferentes pendientes, colocados espalda con espalda (arriba) como en un prisma. Un collar con cuentas situadas a intervalos iguales se coloca sobre los planos inclinados, con una parte colgando por debajo. Las cuentas que descansan sobre los planos actúan como cargas sobre los planos, sostenidas por la fuerza de tensión que experimenta la cuerda en el punto "T". El argumento de Stevin es el siguiente:^[5]^[6]^[7]

La cadena debe estar quieta, en equilibrio mecánico. Si fuera más pesada de un lado que del otro, y comenzara a deslizarse hacia la derecha o hacia la izquierda por su propio peso, cuando cada cuenta se hubiera movido a la posición de la cuenta anterior, la cuerda sería indistinguible de su posición inicial y, por lo tanto, continuaría estando desequilibrada y deslizante. Este argumento podría repetirse indefinidamente, dando como resultado una situación de móvil perpetuo circular, lo que es absurdo. Por lo tanto, permanece estacionaria, con las fuerzas en los dos lados del punto T (arriba) iguales.
La parte de la cadena que cuelga debajo de los planos inclinados es simétrica, con igual número de cuentas a cada lado. Ejerce una fuerza igual en cada lado de la cuerda. Por lo tanto, esta porción de la cuerda se puede cortar en los bordes de los planos (puntos S y V), dejando solo las cuentas descansando en los planos inclinados, y esta porción restante aún estará en equilibrio estático.
Dado que las cuentas están situadas a intervalos iguales en el collar, el número total de cuentas soportadas por cada plano, la carga total, es proporcional a la longitud del plano. Dado que la fuerza de soporte de entrada, la tensión en el hilo del collar, es la misma a ambos lados, la ventaja mecánica de cada plano es proporcional a su longitud inclinada.

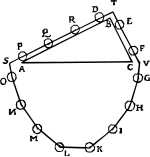
Como señaló Dijksterhuis, el argumento de Stevin^[8] no es completamente estricto. Las fuerzas ejercidas por la parte colgante de la cadena no necesitan ser simétricas porque la parte colgante “no necesita conservar su forma” cuando se suelta. Incluso si la cadena se suelta con un momento angular cero, el movimiento, incluidas las oscilaciones, es posible a menos que la cadena esté inicialmente en su configuración de equilibrio, una suposición que haría que el argumento fuera circular.

Se han utilizado planos inclinados desde tiempos prehistóricos para mover objetos pesados.^[9]^[10] Los caminos inclinados y los pedraplenes construidos por civilizaciones antiguas como los romanos son ejemplos de los primeros planos inclinados que han sobrevivido y muestran que entendieron el valor de este dispositivo para mover cargas cuesta arriba. Se cree que las piedras pesadas utilizadas en estructuras de piedra antiguas como Stonehenge^[11] se movieron y colocaron en su lugar usando planos inclinados hechos de tierra,^[12] aunque es difícil encontrar evidencia de tales rampas de construcción temporales. Las pirámides de Egipto se construyeron utilizando planos inclinados, y rampas de asedio^[13]^[14]^[15] permitieron a los ejércitos antiguos superar las murallas de las fortalezas. Los antiguos griegos construyeron una rampa pavimentada de 6 km (3,7 millas) de largo, el Diolkos, para arrastrar barcos por tierra a través del istmo de Corinto.^[16]

Sin embargo, el plano inclinado fue la última de las seis máquinas simples clásicas en ser reconocida como tal. Esto probablemente se deba a que es un dispositivo pasivo e inmóvil (la carga es la parte móvil),^[17] y también a que se encuentra en la naturaleza en forma de pendientes y colinas. Aunque entendieron su uso para levantar objetos pesados, los filósofos de la antigua Grecia que definieron las otras cinco máquinas simples, no incluyeron el plano inclinado.^[18] Este punto de vista persistió entre algunos científicos posteriores; y en una fecha tan tardía como 1826 Karl von Langsdorf escribió que un plano inclinado "... no es más una máquina que la pendiente de una montaña".^[17] El problema de calcular la fuerza requerida para empujar un peso hacia arriba en un plano inclinado (su ventaja mecánica) fue analizado por los filósofos griegos Herón de Alejandría (c. 10 - 60 EC) y Papo de Alejandría (c. 290 - 350 EC), pero ambos se equivocaron en su resolución.^[19]^[20]^[21]

No fue hasta el Renacimiento cuando el plano inclinado se resolvió matemáticamente y se clasificó con las otras máquinas simples. El primer análisis correcto del plano inclinado apareció en la obra del enigmático autor del siglo XIII Jordanus Nemorarius,^[22]^[23] aunque su solución del problema aparentemente no fue comunicada a otros filósofos de la época.^[20] Gerolamo Cardano (1570) propuso la solución incorrecta de que la fuerza a aplicar es proporcional al ángulo del plano.^[5] Posteriormente, a finales del siglo XVI, Michael Varro (1584), Simon Stevin (1586) y Galileo Galilei (1592) publicaron tres soluciones correctas a lo largo de diez años.^[20] Aunque no fue la primera, la deducción del ingeniero flamenco Simon Stevin^[21] es la más conocida, por su originalidad y el uso de un collar de cuentas (véase el recuadro).^[7]^[22] En 1600, el científico italiano Galileo incluyó el plano inclinado en su análisis de máquinas simples en Le Meccaniche ("Sobre la mecánica"), mostrando su similitud subyacente con las otras máquinas como un amplificador de fuerza.^[24]

Las primeras reglas elementales para deslizar objetos con fricción sobre un plano inclinado fueron descubiertas por Leonardo da Vinci (1452-1519), pero quedaron inéditas en sus cuadernos.^[25] Fueron redescubiertas por Guillaume Amontons (1699) y Charles-Augustin de Coulomb (1785) las desarrolló aún más.^[25] Leonhard Euler (1750) demostró que la tangente del ángulo de rozamiento interno en un plano inclinado es proporcional a la fricción.^[26]

Referencias

↑ Tipler, Paul Allen (1991). Física preuniversitaria. Reverte. ISBN 9788429143751. Consultado el 20 de febrero de 2018.
↑ Ignacio, Ramírez Vargas; Manuel, Palacios Pineda, Luis; E, Rodríguez C. , Mario. Estática para ingeniería. Grupo Editorial Patria. ISBN 9786077442691. Consultado el 20 de febrero de 2018.
↑ ^a ^b Fisica Volumen i. Pearson Educación. 2006. ISBN 9789702607762. Consultado el 20 de febrero de 2018.
↑ Tipler, Paul Allen; Mosca, Gene (2005). Física para la ciencia y la tecnología. Reverte. ISBN 9788429144116. Consultado el 20 de febrero de 2018.
↑ ^a ^b ^c Koetsier, Teun (2010). «Simon Stevin and the rise of Archimedean mechanics in the Renaissance». The Genius of Archimedes – 23 Centuries of Influence on Mathematics, Science and Engineering: Proceedings of an International Conference Held at Syracuse, Italy, June 8–10, 2010. Springer. pp. 94-99. ISBN 978-90-481-9090-4.
↑ Devreese, Jozef T.; Guido Vanden Berghe (2008). 'Magic is no magic': The wonderful world of Simon Stevin. WIT Press. pp. 136-139. ISBN 978-1-84564-391-1.
↑ ^a ^b Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1963). The Feynman Lectures on Physics, Vol. I. USA: California Inst. of Technology. pp. 4.4-4.5. ISBN 978-0-465-02493-3.
↑ E.J.Dijksterhuis: Simon Stevin 1943
↑ Therese McGuire, Light on Sacred Stones, in Conn, Marie A.; Therese Benedict McGuire (2007). Not etched in stone: essays on ritual memory, soul, and society. University Press of America. p. 23. ISBN 978-0-7618-3702-2.
↑ Dutch, Steven (1999). «Pre-Greek Accomplishments». Legacy of the Ancient World. Prof. Steve Dutch's page, Univ. of Wisconsin at Green Bay. Consultado el March 13, 2012.
↑ Moffett, Marian; Michael W. Fazio; Lawrence Wodehouse (2003). A world history of architecture. Laurence King Publishing. p. 9. ISBN 978-1-85669-371-4.
↑ Peet, T. Eric (2006). Rough Stone Monuments and Their Builders. Echo Library. pp. 11-12. ISBN 978-1-4068-2203-8.
↑ Thomas, Burke (2005). «Transport and the Inclined Plane». Construction of the Giza Pyramids. world-mysteries.com. Consultado el March 10, 2012.
↑ Isler, Martin (2001). Sticks, stones, and shadows: building the Egyptian pyramids. USA: University of Oklahoma Press. pp. 211–216. ISBN 978-0-8061-3342-3. (requiere registro).
↑ Sprague de Camp, L. (1990). The Ancient Engineers. USA: Barnes & Noble. p. 43. ISBN 978-0-88029-456-0.
↑ Error en la cita: Etiqueta <ref> no válida; no se ha definido el contenido de las referencias llamadas Silverman
↑ ^a ^b Karl von Langsdorf (1826) Machinenkunde, quoted in Reuleaux, Franz (1876). The kinematics of machinery: Outlines of a theory of machines. MacMillan. pp. 604.
↑ for example, the lists of simple machines left by Roman architect Vitruvius (c. 80 – 15 BCE) and Greek philosopher Herón de Alejandría (c. 10 – 70 CE) consist of the five classical simple machines, excluding the inclined plane. – Smith, William (1848). Dictionary of Greek and Roman antiquities. London: Walton and Maberly; John Murray. p. 722. , Usher, Abbott Payson (1988). A History of Mechanical Inventions. USA: Courier Dover Publications. pp. 98, 120. ISBN 978-0-486-25593-4.
↑ Heath, Thomas Little (1921). A History of Greek Mathematics, Vol. 2. UK: The Clarendon Press. pp. 349, 433–434.
↑ ^a ^b ^c Egidio Festa and Sophie Roux, The enigma of the inclined plane in Laird, Walter Roy; Sophie Roux (2008). Mechanics and natural philosophy before the scientific revolution. USA: Springer. pp. 195-221. ISBN 978-1-4020-5966-7.
↑ ^a ^b Meli, Domenico Bertoloni (2006). Thinking With Objects: The Transformation of Mechanics in the Seventeenth Century. JHU Press. pp. 35-39. ISBN 978-0-8018-8426-9.
↑ ^a ^b Boyer, Carl B.; Uta C. Merzbach (2010). A History of Mathematics, 3rd Ed.. John Wiley and Sons. ISBN 978-0-470-63056-3.
↑ Usher, Abbott Payson (1988). A History of Mechanical Inventions. Courier Dover Publications. p. 106. ISBN 978-0-486-25593-4.
↑ Machamer, Peter K. (1998). The Cambridge Companion to Galileo. London: Cambridge University Press. pp. 47-48. ISBN 978-0-521-58841-6.
↑ ^a ^b Armstrong-Hélouvry, Brian (1991). Control of machines with friction. USA: Springer. p. 10. ISBN 978-0-7923-9133-3.
↑ Meyer, Ernst (2002). Nanoscience: friction and rheology on the nanometer scale. World Scientific. p. 7. ISBN 978-981-238-062-3.

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre planos inclinados.

Datos: Q161462
Multimedia: Inclined planes / Q161462

[1] Tipler, Paul Allen (1991). Física preuniversitaria. Reverte. ISBN 9788429143751. Consultado el 20 de febrero de 2018.

[2] Ignacio, Ramírez Vargas; Manuel, Palacios Pineda, Luis; E, Rodríguez C. , Mario. Estática para ingeniería. Grupo Editorial Patria. ISBN 9786077442691. Consultado el 20 de febrero de 2018.

[:0-3] Fisica Volumen i. Pearson Educación. 2006. ISBN 9789702607762. Consultado el 20 de febrero de 2018.

[4] Tipler, Paul Allen; Mosca, Gene (2005). Física para la ciencia y la tecnología. Reverte. ISBN 9788429144116. Consultado el 20 de febrero de 2018.

[Koetsier-5] Koetsier, Teun (2010). «Simon Stevin and the rise of Archimedean mechanics in the Renaissance». The Genius of Archimedes – 23 Centuries of Influence on Mathematics, Science and Engineering: Proceedings of an International Conference Held at Syracuse, Italy, June 8–10, 2010. Springer. pp. 94-99. ISBN 978-90-481-9090-4.

[Devreese-6] Devreese, Jozef T.; Guido Vanden Berghe (2008). 'Magic is no magic': The wonderful world of Simon Stevin. WIT Press. pp. 136-139. ISBN 978-1-84564-391-1.

[Feynman-7] Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1963). The Feynman Lectures on Physics, Vol. I. USA: California Inst. of Technology. pp. 4.4-4.5. ISBN 978-0-465-02493-3.

[8] E.J.Dijksterhuis: Simon Stevin 1943

[Conn-9] Therese McGuire, Light on Sacred Stones, in Conn, Marie A.; Therese Benedict McGuire (2007). Not etched in stone: essays on ritual memory, soul, and society. University Press of America. p. 23. ISBN 978-0-7618-3702-2.

[Dutch-10] Dutch, Steven (1999). «Pre-Greek Accomplishments». Legacy of the Ancient World. Prof. Steve Dutch's page, Univ. of Wisconsin at Green Bay. Consultado el March 13, 2012.

[Moffett-11] Moffett, Marian; Michael W. Fazio; Lawrence Wodehouse (2003). A world history of architecture. Laurence King Publishing. p. 9. ISBN 978-1-85669-371-4.

[Peet-12] Peet, T. Eric (2006). Rough Stone Monuments and Their Builders. Echo Library. pp. 11-12. ISBN 978-1-4068-2203-8.

[Thomas-13] Thomas, Burke (2005). «Transport and the Inclined Plane». Construction of the Giza Pyramids. world-mysteries.com. Consultado el March 10, 2012.

[Isler-14] Isler, Martin (2001). Sticks, stones, and shadows: building the Egyptian pyramids. USA: University of Oklahoma Press. pp. 211–216. ISBN 978-0-8061-3342-3. (requiere registro).

[SpragueDeCamp-15] Sprague de Camp, L. (1990). The Ancient Engineers. USA: Barnes & Noble. p. 43. ISBN 978-0-88029-456-0.

[Silverman-16] Error en la cita: Etiqueta <ref> no válida; no se ha definido el contenido de las referencias llamadas Silverman

[Reuleaux-17] Karl von Langsdorf (1826) Machinenkunde, quoted in Reuleaux, Franz (1876). The kinematics of machinery: Outlines of a theory of machines. MacMillan. pp. 604.

[18] r example, the lists of simple machines left by Roman architect Vitruvius (c. 80 – 15 BCE) and Greek philosopher Herón de Alejandría (c. 10 – 70 CE) consist of the five classical simple machines, excluding the inclined plane. – Smith, William (1848). Dictionary of Greek and Roman antiquities. London: Walton and Maberly; John Murray. p. 722. , Usher, Abbott Payson (1988). A History of Mechanical Inventions. USA: Courier Dover Publications. pp. 98, 120. ISBN 978-0-486-25593-4.

[19] Heath, Thomas Little (1921). A History of Greek Mathematics, Vol. 2. UK: The Clarendon Press. pp. 349, 433–434.

[Laird-20] Egidio Festa and Sophie Roux, The enigma of the inclined plane in Laird, Walter Roy; Sophie Roux (2008). Mechanics and natural philosophy before the scientific revolution. USA: Springer. pp. 195-221. ISBN 978-1-4020-5966-7.

[Meli-21] Meli, Domenico Bertoloni (2006). Thinking With Objects: The Transformation of Mechanics in the Seventeenth Century. JHU Press. pp. 35-39. ISBN 978-0-8018-8426-9.

[Boyer-22] Boyer, Carl B.; Uta C. Merzbach (2010). A History of Mathematics, 3rd Ed.. John Wiley and Sons. ISBN 978-0-470-63056-3.

[Usher-23] Usher, Abbott Payson (1988). A History of Mechanical Inventions. Courier Dover Publications. p. 106. ISBN 978-0-486-25593-4.

[Machamer-24] Machamer, Peter K. (1998). The Cambridge Companion to Galileo. London: Cambridge University Press. pp. 47-48. ISBN 978-0-521-58841-6.

[Armstrong-25] Armstrong-Hélouvry, Brian (1991). Control of machines with friction. USA: Springer. p. 10. ISBN 978-0-7923-9133-3.

[Meyer-26] Meyer, Ernst (2002). Nanoscience: friction and rheology on the nanometer scale. World Scientific. p. 7. ISBN 978-981-238-062-3.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]