Diferencia entre revisiones de «Teorema del coseno»
Deshecha la edición 29201976 de 193.152.187.78 (disc.) |
|||
| Línea 1: | Línea 1: | ||
{{AP|Teorema del coseno}} |
|||
{{Artículo bueno}} |
|||
El objetivo de este apéndice es presentar pruebas de algunas afirmaciones usadas en el artículo [[Teorema del coseno]], pero que por razones didácticas es preferible separar del cuerpo principal, ya que incluirlas directamente interrumpiría el flujo de la explicación con digresiones no relacionadas directamente con el tema central de la exposición. |
|||
== Area de un paralelogramo == |
|||
El '''teorema del coseno''' es una generalización del [[teorema de Pitágoras]] en los triángulos no rectángulos que se utiliza, normalmente, en [[trigonometría]]. |
|||
[[Imagen:Area de paralelogramo.svg|thumb|svg|Deducción del teorema sobre área de un paralelogramo.]] |
|||
Se afirma: |
|||
{{Teorema|Un paralelogramo cuyos lados miden ''a'' y ''b'', formando un ángulo de 90°-γ, tiene un área de ''ab'' cos(γ).}} |
|||
Consideremos un paralelogramo de lados ''a'' y ''b'', formando un ángulo de θ, como n el diagrama. |
|||
El teorema relaciona un lado de un triángulo con los otros dos y con el [[coseno]] del [[ángulo]] formado por estos dos lados: |
|||
Dividamos el paralelogramo por medio de una diagonal para obtener dos zonas triangulares. En una de ellas, dibujemos una altura ''h'' como se muestra en la figura. |
|||
La zona triangular roja tiene por área ''ah/2''. Por definición, sin(θ)=''h/b'', de modo que ''h=b'' sin(θ). La sustitución en la fórmula del área triangular prueba que: |
|||
{{Teorema|Dado un triángulo ABC, siendo α, β, γ, los ángulos, y ''a'', ''b'', ''c'', los lados respectivamente opuestos a estos ángulos entonces: {{Ecuación|<math>c^2=a^2+b^2-2ab\,\cos(\gamma)</math>}}}} |
|||
{{Teorema|El área de un triángulo en donde dos lados de medidas ''a'' y ''b'' forman un ángulo de θ es |
|||
: <math> A_T=\frac{ab\, \cos\theta}{2}</math> |
|||
}} |
|||
Dado que el área del paralelogramo es el doble del triángulo, se concluye que |
|||
En la mayoría de los idiomas, este teorema es conocido con el nombre de '''teorema del coseno''', denominación no obstante relativamente tardía. En [[idioma francés|francés]], sin embargo, lleva el nombre del [[matemático]] [[imperio Persa|persa]] [[Ghiyath al-Kashi]] que unificó los resultados de sus predecesores.<ref>{{cita publicación | autor = Kennedy, E S ; Debarnot, M.- T | título = Al-Kashi's Impractical Method of Determining the Solar Altitude | año = 1979| publicación = Journal for the History of Arabic Science Aleppo | volumen = 3| número = 2| id = pag 219-227| url = http://cat.inist.fr/?aModele=afficheN&cpsidt=12569968}}</ref> |
|||
{{Teorema|El área de un paralelogramo de lados ''a'' y ''b'' formando un ángulo de θ es |
|||
: <math> A_P=ab\, \cos\theta</math> |
|||
}} |
|||
La conclusión se sigue notando que si θ=90-γ entonces sen(θ)=sen(90°-γ) = cos(γ). Se hace notar también que la demostración es independiente de cual de las diagonales del paralelogramo se escoja, puesto que sen(θ)=sen(180°-θ). |
|||
[[Archivo:Triangle with notations 2.svg|thumb|280px|right|Fig. 1 - Notación más habitual de un triángulo.]] |
|||
''' |
|||
== Historia == |
|||
== Texto en negrita == |
|||
la matematica no sirve para nada'''== Cuerdas en un círculo == |
|||
[[Imagen:Cosenos por potencia de un punto.svg|thumb|Diagrama usado en la prueba basada en [[potencia de un punto]]]] |
|||
En la demostración del Teorema del coseno usando [[potencia de un punto]], se afirma que el segmento ''CK'' en el diagrama mide precisamente -2''a'' cos(γ). |
|||
La demostración más sencilla consiste en prolongar el segmento ''CB'' hasta cortar nuevamente la circunferencia en un punto ''D'', de modo que ''CD'' es un diámetro del círculo, puesto que pasa por el centro del mismo. |
|||
''[[Los Elementos]]'' de [[Euclides]], que datan del [[siglo III a. C.|siglo III a. C.]], contienen ya una aproximación geométrica de la generalización del [[teorema de Pitágoras]]: las proposiciones 12 y 13 del [[Libro II de los Elementos de Euclides|libro II]], tratan separadamente el caso de un [[triángulo#Tipos de triángulos|triángulo obtusángulo]] y el de un [[triángulo#Tipos de triángulos|triángulo acutángulo]]. |
|||
La formulación de la época es arcaica ya que la ausencia de [[función trigonométrica|funciones trigonométricas]] y del [[álgebra]] obligó a razonar en términos de diferencias de áreas.<ref> |
|||
{{cita libro | apellidos = Heath | nombre = Sir Thomas | título = A history of Greek Mathematics vol. 1 | año = 1921 | editorial = Londres, Inglaterra: Oxford University Press | idioma=inglés | id = {{OCLC|2014918}} }}</ref> Por eso, la proposición 12 utiliza estos términos: |
|||
{{cita|«En los triángulos obtusángulos, el cuadrado del lado opuesto al ángulo obtuso es mayor que los cuadrados de los lados que comprenden el ángulo obtuso en dos veces el rectángulo comprendido por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso.» |Euclides, ''Elementos''.|<ref>{{cita web|url=http://www.euclides.org/menu/elements_esp/02/proposicioneslibro2.htm#12|título=Proposición 12 del libro II de Los Elementos de Euclides}}</ref>}} |
|||
Siendo ''ABC'' el triángulo, cuyo ángulo obtuso está en ''C'', y ''BH'' la altura respecto del vértice ''B'' (cf. Fig. 2 contigua), la notación moderna permite formular el enunciado así: |
|||
[[Archivo:obtuse-triangle-with-altitude.png|thumb|Fig. 2 - Triángulo ''ABC'' con altura ''BH''.]] |
|||
{{Ecuación|<math>AB^2 = zCA^2 + CB^2 + 2\ CA\ CH</math>}} |
|||
Faltaba esperar la trigonometría árabe-musulmana de la [[Edad Media]] para ver al teorema evolucionar a su forma y en su alcance: el [[astrónomo]] y matemático [[al-Battani]]<ref>{{cita web|url=http://ing.unne.edu.ar/Matem_diccion/p1105_historia_de_%20la_matematica.pdf|título=Esquema del desarrollo histórico de la matemática|editorial=[[Universidad Nacional del Nordeste]]|páginas=pág. 6}}</ref> generalizó el resultado de Euclides en la geometría esférica a principios del [[siglo X]], lo que permitió efectuar los cálculos de la distancia angular entre el [[Sol]] y la [[Tierra]].<ref>{{cita web |url= http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Battani.html |título= Abu Abdallah Mohammad ibn Jabir Al-Battani |fechaacceso= 2008-06-08 |autor= J J O'Connor y E F Robertson|formato= html |idioma= inglés }}</ref><ref>{{cita web |url= http://www.mallorcaweb.net/mamaguena/arabs/trigo/trigo.html |título=La trigonometria àrab, Al-Battani, Abu’l-Wafa, Ibn Yunus, Nasir al-Tusi |fechaacceso= 2008-06-08 |formato= html |idioma= catalán }}</ref> Fue durante el mismo período cuando se establecieron las primeras tablas trigonométricas, para las funciones [[trigonometría|seno]] y [[coseno]]. Eso permitió a [[Ghiyath al-Kashi]],<ref>{{cita web|url=http://serge.mehl.free.fr/chrono/Alkashi.html|título=Al-Kashi, Gamshid ibn Messaoud|idioma = francés}}</ref> matemático de la escuela de [[Samarcanda]], de poner el teorema bajo una forma utilizable para la [[triangulación]] durante el [[siglo XV]]. La propiedad fue popularizada en occidente por [[François Viète]] quien, al parecer, lo redescubrió independientemente.<ref>{{cita libro|título= Canon mathematicus seu ad triangula |apellidos= Viète|nombre=François |año = 1579 | editorial = Lutetia Mettayer |id= {{OCLC|165919384}} }}</ref> |
|||
Fue a finales del [[siglo XVII]] cuando la notación algebraica moderna, aunada a la notación moderna de las funciones trigonométricas introducida por [[Leonhard Euler|Euler]] en su libro ''Introductio in analysin infinitorum'', permitieron escribir el teorema bajo su forma actual, extendiéndose el nombre de teorema (o ley) del coseno.<ref>{{cita libro|título= A History of Mathematics|apellidos= Boyer|nombre=Carl B.|coautores= Uta C. Merzbach |año = 1968 | editorial = New York: Estados Unidos: John Wiley & Sons|isbn= 0-471-54397-7 |páginas= 439–445}}</ref> |
|||
== El teorema y sus aplicaciones == |
|||
El teorema del coseno es también conocido por el nombre de '''teorema de Pitágoras generalizado''', ya que el [[teorema de Pitágoras]] es un caso particular: cuando el ángulo <math>\gamma \,</math> es recto o, dicho de otro modo, cuando <math>\cos\gamma = 0 \,</math>, el teorema del coseno se reduce a: |
|||
{{Ecuación|<math>\,c^2=a^2+b^2</math>}} |
|||
que es precisamente la formulación del teorema de Pitágoras. |
|||
[[Archivo:Triángulo con un ángulo o un lado desconocido.svg|thumb|Fig. 3 - Utilización del teorema del coseno: ángulo o lado desconocido.]] |
|||
El teorema se utiliza en [[triangulación]] (ver Fig. 3) para resolver un triángulo, y saber determinar |
|||
* el tercer lado de un triángulo cuando conocemos un ángulo y los lados adyacentes: |
|||
{{Ecuación|<math>c = \sqrt{a^2+b^2-2ab\cos\gamma}</math>.}} |
|||
* los ángulos de un triángulo cuando conocemos los tres lados: |
|||
{{Ecuación|<math>\gamma = \arccos \frac{a^2+b^2-c^2}{2ab}</math>.}} |
|||
Estas fórmulas son difíciles de aplicar en el caso de mediciones de triángulos muy agudos utlizando métodos simples, es decir, cuando el lado ''c'' es muy pequeño respecto los lados ''a'' y ''b'' —o su equivalente, cuando el ángulo ''γ'' es muy pequeño. |
|||
Existe un corolario del teorema del coseno para el caso de dos triángulos semejantes ABC y <nowiki>A'B'C'</nowiki> |
|||
{{Ecuación|<math>\,cc' = aa' + bb' - (ab'+a' b)\cos\gamma</math>.}} |
|||
== Demostraciones == |
|||
=== Por desglose de áreas === |
|||
[[Archivo:Ley de cosenos con ángulo agudo.svg|thumb|280px|Fig. 4a - Demostración del teorema del coseno por desglose de áreas, cuando el ángulo es agudo.]]Un cierto número de la demostraciones del teorema hacen intervenir un cálculo de [[área (Geometría)|áreas]]. Conviene en efecto remarcar que |
|||
* ''a², b², c²'' son las áreas de los [[cuadrado]]s de lados respectivos ''a, b, c''. |
|||
* ''ab'' cos(γ) es el área de un paralelogramo de lados ''a'' y ''b'' que forman un ángulo de 90°-γ (para una prueba, ver el [[Teorema del coseno/apéndice|apéndice]]). |
|||
Dado que cos(γ) cambia de signo dependiendo de si γ es mayor o menor a 90°, se hace necesario dividir la prueba en 2 casos |
|||
La figura 4a (contigua) divide un heptágono de dos maneras diferentes para demostrar el teorema del coseno en el caso de un ángulo agudo. La división es la siguiente: |
|||
* En verde, las áreas ''a², b² la izquierda, y el área , ''c²'' a la derecha. |
|||
* En rojo, el triángulo ''ABC'' en ambos diagramas y en amarillo triángulos congruentes al ''ABC''. |
|||
* En azul, paralelogramos de lados ''a'' y ''b'' con ángulo ''90''°-γ. |
|||
Igualando las áreas y cancelando las figuras iguales se obtiene que <math>a^2+b^2 = c^2+2ab\, \cos\gamma</math>, equivalente al Teorema del coseno. |
|||
<br clear="all"/> |
|||
[[Archivo:Ley de cosenos con ángulo obtuso.svg|thumb|280px|Fig. 4b - Demostración del teorema del coseno por desglose de áreas, cuando el ángulo es obtuso.]] |
|||
La figura 4b (contigua) desglosa un hexágono de dos maneras diferentes para demostrar el teorema del coseno en el caso de un ángulo obtuso. La figura muestra |
|||
* En verde ''a², b²'' la izquierda y ''c²'' a la derecha. |
|||
* En azul -''2ab'' cos(γ), recordando que al ser cos(γ) negativo, la expresión completa es positiva. |
|||
* En rojo, dos veces el triángulo ''ABC'' para ambos lados de la figura. |
|||
Igualando áreas y cancelando las zonas rojas da <math>\,a^2+b^2-2ab\cos\gamma = c^2</math>, como queríamos demostrar. |
|||
<br clear="all"/> |
|||
=== Por el teorema de Pitágoras === |
|||
Notemos que el Teorema de Cosenos es equivalente al Teorema de Pitágoras cuando el ángulo <math>\gamma</math> es recto. Por tanto sólo es necesario considerar los casos cuando ''c'' es adyacente a dos ángulos agudos y cuando ''c'' es adyacente a un ángulo agudo y un obtuso. |
|||
'''Primer caso:''' ''c'' es adyacente a dos ángulos agudos. [[Archivo:CosenosPorPitagoras1.svg|thumb|Caso 1: ''c'' es adyacente a dos ángulos agudos]] |
|||
Consideremos la figura adjunta. El teorema de Pitágoras establece que ''c² = h² + u²'' de modo que ''h² = a² - (b-u)²''. |
|||
Combinando ambas ecuaciones y luego simplificando obtenemos ''c² = u² + a² - b² + 2bu - u²'', es decir: |
|||
{{Ecuación|<math>c^2 = a^2 - b^2 + 2bu\,</math>|3=left}} |
|||
Por la definición de coseno, se tiene cos(γ) = (b-u)/a, por tanto |
|||
{{Ecuación|<math> u = b- a \,\cos\gamma\,</math>|3=left}} |
|||
Sustituimos el valor de u en la expresión para ''c²'' y simplificamos: ''c² = a²-b² +2b ''(''b-a ''cos(γ)), concluyendo |
|||
{{Ecuación|<math> c^2 = a^2 +b^2 -2ab\, \cos \gamma</math>|3=left}} |
|||
y terminando con esto la prueba del primer caso. |
|||
'''Segundo caso:''' ''c'' es adyacente a un ángulo obtuso. [[Archivo:CosenosPorPitagoras2.svg|thumb|Caso 2: ''c'' es adyacente a un ángulo obtuso]] |
|||
Consideremos la figura adjunta. El teorema de Pitágoras establece nuevavamente ''c² = h² + u²'' pero en este caso ''h² = a² - (b+u)²''. Combinando ambas ecuaciones obtenemos <math> c^2 = u^2 + a^2 - b^2 - 2bu - u^2 </math> y de este modo: |
|||
{{Ecuación|<math>c^2 = a^2 -b^2 -2bu\,</math>.|3=left}} |
|||
De la definición de coseno, se tiene cos(γ) = (b+u)/a y por tanto |
|||
{{Ecuación|<math> u = a\, \cos\gamma -b\,</math>.|3=left}} |
|||
Sustituimos en la expresión para ''c²'' y simplificamos ''c² = a²-b² -2b''(''a'' cos(γ)-''b''), concluyendo nuevamente |
|||
{{Ecuación|<math> c^2 = a^2 +b^2 -2ab\, \cos \gamma\,</math>.|3=left}} |
|||
Esto concluye la demostración. |
|||
Es importante notar, que si se considera a ''u'' como un segmento dirigido, entonces sólo hay un caso y las dos demostraciones se convierten en la misma. |
|||
<br clear="all"/> |
|||
=== Por la potencia de un punto con respecto a un círculo === |
|||
[[Archivo:Cosenos por potencia de un punto.svg|thumb|Fig. 6 - Demostración del teorema del coseno utilizando la [[potencia de un punto]] con respecto a un círculo.]] |
|||
Consideremos un círculo con centro en ''B'' y radio ''BC'', como en la figura 6. Si ''AC'' es tangente al círculo, nuevamente se tiene el Teorema de Pitágoras. Cuando ''AC'' no es tangente, existe otro punto ''K'' de corte con el círculo. LA [[potencia de un punto|potencia]] del punto A con respecto a dicho círculo es |
|||
{{Ecuación|<math>AP\cdot AL=AC\cdot AK= AC (AC+CK)</math>.|3=left}} |
|||
Por otro lado, ''AL = c+a'' y ''AP = c-a'' de modo que |
|||
{{Ecuación|<math>AP\cdot AL = (c+a)(c-a) = c^2 -a^2</math>.|3=left}} |
|||
Además, ''CK= -2a cos(γ)'' (ver el [[Teorema del coseno/apéndice|apéndice]]) por lo que |
|||
{{Ecuación|<math>AC(AC+CK) = b(b -2a\,cos(\gamma))</math>.|3=left}} |
|||
Igualando las expresiones obtenidas se obtiene nuevamente ''c²=a²+b²-2ab cos(γ)''. |
|||
Contrariamente a las precedentes, para esta demostración, no es necesario recurrir a un estudio por caso pues las relaciones algebraicas son las mismas para el caso del ángulo agudo. |
|||
<br clear="all"/> |
|||
=== Por el cálculo vectorial === |
|||
Utilizando el cálculo [[vector (matemática)|vectorial]], más precisamente el [[producto escalar]], es posible encontrar el teorema del coseno en algunas líneas: |
|||
:{| border=0 |
|||
|<math>c^2\,</math> |
|||
|<math>=\lVert\overrightarrow{\mathrm{AB}}\lVert^2</math> |
|||
|- |
|||
| |
|||
|<math>= \lVert\overrightarrow{\mathrm{CB}}-\overrightarrow{\mathrm{CA}}\lVert^2</math> |
|||
|- |
|||
| |
|||
|<math>=\lVert\overrightarrow{\mathrm{CB}}\lVert^2-2\cdot\overrightarrow{\mathrm{CB}}\cdot\overrightarrow{\mathrm{CA}}+\lVert\overrightarrow{\mathrm{CA}}\lVert^2</math> |
|||
|- |
|||
| |
|||
|<math>=\mathrm{CB}^2-2\cdot\left|\mathrm{CB}\right|\cdot\left|\mathrm{CA}\right|\cos\widehat{\mathrm{ACB}}+\mathrm{CA}^2</math> |
|||
|- |
|||
| |
|||
|<math>=a^2+b^2-2ab \cos\gamma\, </math> |
|||
|} |
|||
== Generalización en geometrías no euclídeas == |
|||
[[Archivo:Spherical_triangle_with_notations.png|thumb|200px|Fig. 7 - Triángulo esférico: dimensiones reducidas ''a'', ''b'' y ''c'' ; ángulos α, β y γ.]] |
|||
Para una [[geometría no euclídea|superficie no euclídea]] de curvatura ''K'', señalamos con ''R'' el radio de curvatura. Este verifica |
|||
:<math>\,R = 1/\sqrt{|K|}</math>. |
|||
Definimos entonces las dimensiones reducidas del triángulo: |
|||
:<math>\,a = BC/R</math>, |
|||
:<math>\,b = AC/R</math>, |
|||
:<math>\,c = AB/R</math>. |
|||
En el caso de un triángulo esférico, ''a'', ''b'' y ''c'' corresponden a la medida angular de los segmentos de grande arco [BC], [AC] y [AB] (ver Fig. 7). |
|||
<br clear="all"/> |
|||
=== Geometría esférica === |
|||
Cuando el radio de curvatura es muy grande comparado con las dimensiones del triángulo, es decir cuando |
|||
:<math>\,a <\!\!< 1</math>, |
|||
esta expresión se simplifica para dar la versión euclídea del teorema del coseno. Para hacerlo, :<math>\,\cos a = 1 - a^2/2 + O(a^3)</math>, etc. |
|||
Existe una identidad similar que relaciona los tres ángulos: |
|||
:<math>\cos\gamma = - \cos\alpha\,\cos\beta + \sin\alpha\,\sin\beta\,\cos c</math> |
|||
<br clear="all"/> |
|||
=== Geometría hiperbólica === |
|||
En un triángulo hiperbólico ABC, el teorema del coseno se escribe |
|||
:<math>\cosh c = \cosh a\,\cosh b - \sinh a\,\sinh b\,\cos\gamma</math>. |
|||
Cuando el radio de curvatura se vuelve muy grande frente las dimensiones del triángulo, encontramos el teorema del coseno euclídeo a partir de los desarrollos limitados |
|||
:<math>\,\sinh a = a + O(a^3)</math>, etc., |
|||
:<math>\,\cosh a = 1 + a^2/2 + O(a^3)</math>, etc. |
|||
== Generalización en el espacio euclídeo == |
|||
[[Archivo:Tetrahedro con angulos dihedrales.svg|thumb|260px|Fig. 8 - Tetraedro: vértices, caras y ángulos.]] |
|||
Consideremos un [[tetraedro]] A<sub>1</sub>A<sub>2</sub>A<sub>3</sub>A<sub>4</sub> del espacio euclídeo, siendo: |
|||
:<math>\,\mathrm S_k</math> la cara opuesta al vértice <math>\mathrm A_k\ </math>; |
|||
:<math>\,s_k</math> la superficie de <math>\mathrm S_k\ </math>; |
|||
:<math>\,\Delta_k</math> el [[plano (Geometría)|plano]] que contiene a la cara <math>\mathrm S_k\ </math>; |
|||
:<math>\,\theta_{ij}</math> el ángulo [[diedro|diedral]] <math>\widehat{(\Delta_i, \Delta_j)}</math>. |
|||
(La figura 8, contigua, presenta la notación de los vértices, caras y ángulos del tetraedro). |
|||
Entonces, las superficies y ángulos verifican: |
|||
::<math>\,s_4^2 = s_1^2+s_2^2+s_3^2 - 2s_1s_2\cos\theta_{12}\,</math> |
|||
::<math>- 2s_1s_3\cos\theta_{13} - 2s_2s_3\cos\theta_{23}\,</math>. |
|||
<br clear="all"/> |
|||
2ab+a.b(.b)= AC*AS" |
|||
== Véase también == |
|||
* [[Trigonometría]] |
|||
** [[Triangulación]] |
|||
** [[Trigonometría esférica]] |
|||
** [[Función trigonométrica]] |
|||
* [[Geometría]] del [[triángulo]] |
|||
** [[Teorema de Pitágoras]] |
|||
** [[Teorema del seno]] |
|||
* [[Matemático]]s |
|||
** [[Euclides]] |
|||
** [[al-Battani]] |
|||
** [[Ghiyath al-Kashi]] |
|||
** [[François Viète]] |
|||
== Referencias == |
|||
{{Listaref}} |
|||
== Bibliografía == |
|||
* ''[http://www.euclides.org/menu/elements_esp/indiceeuclides.htm Los Elementos]'', [http://www.euclides.org/menu/elements_esp/02/proposicioneslibro2.htm tomo II], Euclides. |
|||
* ''[http://mathworld.wolfram.com/LawofCosines.html Law of cosines]'', en [http://mathworld.wolfram.com Math World] (en [[idioma inglés|inglés]]) |
|||
* {{cita libro |
|||
| apellidos = Éfimov |
|||
| nombre = N. |
|||
| título = Géométrie Supérieure |
|||
| año = 1981 |
|||
| editorial = Moscú : Éditions Mir |
|||
| id = {{OCLC|11732242}} |
|||
}} |
|||
* {{cita libro |
|||
| apellidos = Lions |
|||
| nombre = Jacques Louis |
|||
| título = Petite Encyclopédie des Mathématiques |
|||
| año = 1980 |
|||
| editorial = París : Didier |
|||
| id = {{OCLC|23703843}} |
|||
}} |
|||
Al ser un diámetro, el ángulo inscrito ''CKD'' es necesariamente recto por lo que el triángulo ''CKD'' es rectángulo. El ángulo ''DCK'' mide θ=180°-γ y por definición: |
|||
{{destacado|fr}} |
|||
{{ecuación|<math>\cos(\theta) = \frac{CK}{CD} = \frac{CK}{2a}</math>}} |
|||
{{Destacado|ca}} |
|||
y por tanto |
|||
{{ecuación|<math>CK = 2a \cos(\theta) = 2a\cos(180^\circ - \gamma) = -2a \cos(\gamma)</math>}} |
|||
ya que cos(180°-''x'') = -cos(''x'') para cualquier valor de ''x''. |
|||
[[Categoría:Teoremas de trigonometría|Coseno]] |
|||
[[Categoría:Triángulos]] |
|||
[[Categoría:Apéndices]] |
|||
[[ar:مبرهنة الكاشي]] |
|||
[[bg:Косинусова теорема]] |
|||
[[bs:Kosinusni teorem]] |
|||
[[ca:Teorema del cosinus]] |
|||
[[cs:Kosinová věta]] |
|||
[[da:Cosinusrelation]] |
|||
[[de:Kosinussatz]] |
|||
[[en:Law of cosines]] |
|||
[[eo:Leĝo de kosinusoj]] |
|||
[[fa:قانون کسینوسها]] |
|||
[[fi:Kosinilause]] |
|||
[[fr:Théorème d'Al-Kashi]] |
|||
[[he:משפט הקוסינוסים]] |
|||
[[hu:Koszinusztétel]] |
|||
[[id:Hukum cosinus]] |
|||
[[it:Teorema del coseno]] |
|||
[[ja:余弦定理]] |
|||
[[ka:კოსინუსების თეორემა]] |
|||
[[km:ទ្រឹស្តីបទកូស៊ីនុស]] |
|||
[[ko:코사인 법칙]] |
|||
[[ms:Hukum kosinus]] |
|||
[[nl:Cosinusregel]] |
|||
[[pl:Twierdzenie cosinusów]] |
|||
[[pms:Teorema dël cosen]] |
|||
[[pt:Lei dos cossenos]] |
|||
[[ro:Teorema cosinusului]] |
|||
[[ru:Теорема косинусов]] |
|||
[[sk:Kosínusová veta]] |
|||
[[sl:Kosinusni izrek]] |
|||
[[sq:Teorema e kosinusit]] |
|||
[[sr:Косинусна теорема]] |
|||
[[sv:Cosinussatsen]] |
|||
[[th:กฎของโคไซน์]] |
|||
[[tr:Kosinüs teoremi]] |
|||
[[uk:Теорема косинусів]] |
|||
[[zh:餘弦定理]] |
|||
Revisión del 19:29 13 oct 2009
El objetivo de este apéndice es presentar pruebas de algunas afirmaciones usadas en el artículo Teorema del coseno, pero que por razones didácticas es preferible separar del cuerpo principal, ya que incluirlas directamente interrumpiría el flujo de la explicación con digresiones no relacionadas directamente con el tema central de la exposición.
Area de un paralelogramo
Se afirma:
|
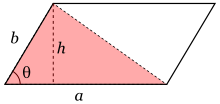
Consideremos un paralelogramo de lados a y b, formando un ángulo de θ, como n el diagrama. Dividamos el paralelogramo por medio de una diagonal para obtener dos zonas triangulares. En una de ellas, dibujemos una altura h como se muestra en la figura.
La zona triangular roja tiene por área ah/2. Por definición, sin(θ)=h/b, de modo que h=b sin(θ). La sustitución en la fórmula del área triangular prueba que:
|
Dado que el área del paralelogramo es el doble del triángulo, se concluye que
|
La conclusión se sigue notando que si θ=90-γ entonces sen(θ)=sen(90°-γ) = cos(γ). Se hace notar también que la demostración es independiente de cual de las diagonales del paralelogramo se escoja, puesto que sen(θ)=sen(180°-θ).
Texto en negrita
la matematica no sirve para nada== Cuerdas en un círculo ==

En la demostración del Teorema del coseno usando potencia de un punto, se afirma que el segmento CK en el diagrama mide precisamente -2a cos(γ).
La demostración más sencilla consiste en prolongar el segmento CB hasta cortar nuevamente la circunferencia en un punto D, de modo que CD es un diámetro del círculo, puesto que pasa por el centro del mismo.
Al ser un diámetro, el ángulo inscrito CKD es necesariamente recto por lo que el triángulo CKD es rectángulo. El ángulo DCK mide θ=180°-γ y por definición:
y por tanto
ya que cos(180°-x) = -cos(x) para cualquier valor de x.




